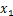机器学习之熵

熵这个词本来是物理学中表示分子混乱程度的物理量，香农(Claude Elwood Shannon)借用过来描述信源的平均不确定性。信息熵的内容在信息论相关教材中有详细的描述，这里仅对机器学习中用到的部分相关概念做个笔记。

1.信息

信息有别于消息，是对事物运动状态或存在方式的不确定性的描述，并且这种不确定性是有大小的。

比如我们在手机上看到这样两则新闻：

科学家通过新技术复活了一只原核细菌。

科学家通过新技术复活了一只恐龙。

听到这两句话的时候，我们内心的波动是不一样的，对于复活的细菌，我们可能看一眼就刷过去了；对于复活的恐龙，我们可能迫不及待的细看一下，如果可以的话，我们也想亲眼见识见识这数千万年前的庞然大物。换言之，这两句话带给我们的信息量是不同的，原核生物复活的可能性大，信息量就小；恐龙复活的可能性小，信息量就大。

2.自信息量

那么信息量的大小如何度量呢？前面说到信息是对事物不确定性的描述，不确定性与事件发生的概率有关，概率越小，不确定性越大，事件发生后所含的信息量就越大。

设事件 $x$ 的概率为 $p$ ,则它的自信息量为

$\large I(x)=log\frac{1}{p(x)}=-logp(x)$ $\small I(x)$ 代表两种含义：在事件发生以前，表示事件 $\small x$ 发生的不确定性的大小；在事件发生以后，表示事件 $\small x$ 所包含的信息量。

式中对数的底可任取，

底为2时，单位为比特 (bit);
底为e时，单位为奈特 (nat);
底为10时，单位为哈特 (hart).

一般取2为底，常省略。

注：因为我们考察的只是一个随机事件本身的信息量，所以称为自信息，如果考察两个事件的相互影响，则为互信息。互信息我们未使用，暂且不谈。

3.信息熵—平均自信息量

信息熵是对系统平均不确定性的描述。从概率统计的角度，信息熵就是随机变量 $X$ 的函数 $\small log(\frac{1}{p})$ 的期望，也就是所有事件自信息量的加权平均，即

$H(X)=-\sum_{i=1}^{n}p(x_{i})logp(x_{i})$ 其中， $n$ 为 $X$ 的所有可能取值个数。

例：随机变量 $X$ 对应的概率空间为

0.98

0.01

0.01

则 $X$ 的信息熵为

$H(X)=-0.98log0.98-0.01log0.01-0.01log0.01=0.161441 (bit)$

4.联合熵与条件熵

将联合自信息与条件自信息进行平均，便得到联合熵与条件熵。

假设二维随机变量 $XY$ 的概率空间为

$\large \begin{bmatrix} XY\\ P(XY) \end{bmatrix}=\begin{bmatrix} x_{1}y_{1} & ... & x_{i}y_{j} &... &x_{m}y_{n} \\ p_{11} & ... & p_{ij} & ... & p_{mn} \end{bmatrix}$

联合熵定义为联合自信息的数学期望，是二维随机变量 $XY$ 的不确定性的度量

$H(XY)=-\sum_{i=1}^{m}\sum_{j=1}^{n}p(x_{i}y_{j})logp(x_{i}y_{j})$

条件熵 $\small H(Y|X)$ 表示在已知随机变量X的条件下随机变量Y的不确定性。定义为X给定条件下Y的条件概率分布的熵对X的数学期望

$H(Y|X)=\sum_{i=1}^{m}p_{i\cdot }H(Y|X=x_{i})$

其中， $\small H(Y|X=x_{i})=-\sum _{j=1}^{n}p(y_{j}|X=x_{i})logp(y_{j}|X=x_{i})$ ，即为给定 $X=x_{_{i}}$ 的条件下Y的条件概率分布的熵。代入上式展开为

$H(Y|X)=\sum_{i=1}^{m}p_{i\cdot }(-\sum_{j=1}^{n}p(y_{j}|X=x_{i})logp(y_{j}|X=x_{i}))$

$=-\sum_{i=1}^{m}\sum_{j=1}^{n}p(x_{i}y_{j})logp(y_{j}|X=x_{i})$

信息熵与联合熵、条件熵的关系：

$H(XY)=H(X)+H(Y|X)$

5.交叉熵(Cross Entropy)

形式上，交叉熵是一个随机变量的概率分布 $\large p$ 对另一个概率分布 $\large q$ 定义的自信息 $-logq$ 的数学期望，表示为

$\large H(p,q)=-\sum_{i=1}^{n}p_{i}logq_{i}$

如果 $\large p$ 为某个数据集的真实分布， $\large q$ 为非真实的近似分布，交叉熵就表示使用分布 $\large q$ 来消除分布 $\large p$ 的不确定性所需代价的大小。

由吉布斯不等式 $-\sum_{i=1}^{n}p_{i}logp_{i}\leqslant -\sum_{i=1}^{n}p_{i}logq_{i}$ （当 $\small p_{i}=q_{i}$ 时等号成立）知，信息熵是消除系统不确定性所需的最小代价，真实分布与任何其他非真实分布的交叉熵都比其自身的信息熵大。这也就是说，交叉熵能够反映两个分布的差异性大小，交叉熵越小，近似分布 $q$ 就越接近真实分布 $p$ （如果分布 $q$ 就是分布 $p$ 了，那么交叉熵就是信息熵，即 $\small H(p,q)=H(p)$ ，此时消除系统不确定性所需代价达到最小）。所以一些分类算法中经常使用交叉熵作为损失函数。

6.相对熵（K-L散度）

交叉熵间接反映了两个分布的差异性大小，更直接一点，如果用分布 $q$ 近似分布 $p$ ，那么它们的差异性究竟有多大呢？我们可以用两者的相对熵（K-L散度，也就是两者熵之差）来定量衡量。

用分布 $\small q$ 近似真实分布 $\small p$ ，交叉熵为

$H(p,q)=-\sum_{i=1}^{n}p_{i}logq_{i}$

真实分布 $\small p$ 自身的信息熵为

$H(p)=-\sum_{i=1}^{n}p_{i}logp_{i}$

相对熵（K-L散度），即两者熵之差为：

$D_{KL}(p||q)=H(p,q)-H(p)=\sum_{i=1}^{n}p_{i}log\frac{p_{i}}{q_{i}}$ 它恒为正值，直接地衡量了两个分布差异性的大小。

在分类算法中，我们需要评估优化标签和预测值之间的差距，使用KL散度正好合适，只不过 $\small H(p)$ 是固定不变的，所以我们只需要使用前半部分的交叉熵就可以了。也有人将K-L散度称为两个分布的K-L距离，只是它不是对称的，即 $D_{KL} (p||q)\neq D_{KL} (q||p)$ .

参考：

李亦农,李梅《信息论基础教程》
李航《统计学习方法》
简书 https://www.jianshu.com/p/43318a3dc715?from=timeline
知乎 https://www.zhihu.com/question/41252833
维基百科 https://en.wikipedia.org/wiki/Gibbs%27_inequality