网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然的,流量<=容量。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,所有“进入”他们的流量和等于所有从他本身“出去”的流量。
- 最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
- 残量(残余容量):每条边中容量与流量的差
- 反相边:若从点u到v的边容量为c,这条边上有流量f流过(称为正向边),则相当于从v到u有一条容量为0的边,其流量为-f,这条边是反向边。(作用:在有更优决策时,撤销已选的边)
- 残量网络:计算图中每条边的残量得到的网络,称为残量网络,并称残量网络上的s-t路径为增广路。
- 增广: 残量网络中任何一条从s到t的有向道路都对应一条原图中增广路——只要求出该道路中所有残量的最小值d,把对应的所有边上的流量增加d即可,这个过程称为增广。显然,只要残量网络中存在增广路,流量就可以增大。可以证明它的逆命题也成立:如果残量网络中不存在增广路,则当前流就是最大流。这就是著名的增广路定义。
最大流的问题中,容量c和流量f满足的3个性质:
- 容量限制:f(u,v)<=c(u,v)
- 斜对称性:f(u,v)=-f(v,u)
- 流量平衡:从s点流出的净流量=流入t点的净流量
反相边的作用: (此部分摘抄https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html)
举例:
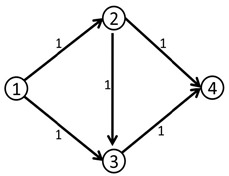
比如说下面这个网络流模型
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。
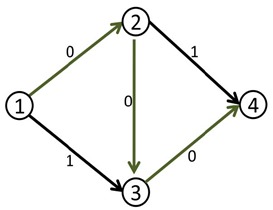
于是我们修改后得到了下面这个流。(图中的数字是容量)
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但是,
这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?
问题就在于我们没有给程序一个“后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。
那么如何解决这个问题呢?
我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。
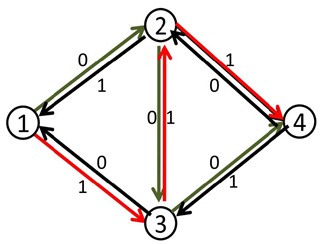
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下:
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
那么,这么做为什么会是对的呢?
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给“退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。
如果这里没有2-4怎么办?
这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点
同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流。
最小割最大流定理:
- s-t割:源点s在集合S中,汇点t在集合T中,起点在S中,终点在T中的集合(S,T)称为s-t割,容量定义为c(S,T)=
(u在S中,v在T中)。
- 最小割:如果将网络中的s-t割包含的边都删去,也就不再有从s到t的路径啦,为保证没有从s到t的路径,需要删去的边的总容量的最小值称为最小割
- 最小割最大流定理:最小割等于最大流。
最大流模板题:
Sample Input
5 4 //5条边,4个点,求从1点到4点的最大流 1 2 40 //点1到点2的容量是40 1 4 20 2 4 20 2 3 30 3 4 10Sample Output
50
EDMONDS-KARP算法(最短增广路算法):
我的理解是:每执行一次bfs增广后,找到最短增广路径,以及对应的把增广值加到对应的增广路径上。
之后再不断地重新启动bfs从源点寻找另一条增广路。
当a[t]==0即从起点到终点的残量值为0时,(不再有增广路了)退出循环。
模拟一下这道题:
- 初始状态,标注为容量:
- 第一次寻找增广路s->t,要增广的值为20,此时图为
- 第二次寻找增广路s->2->t,要增广的值为20,此时图为
- 第三次寻找增广路s->2->3->t,要增广的值为10,此时图为
- 此时无法再找出增广路,结束,答案为50,此时状态如图,标出的是各个边(容量-流量)之值
解释见注释
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
struct Edge{
int from,to,cap,flow;
Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
const int INF=99999999,maxn=210;
int V,E,S,T;
vector<Edge> edges;//存正边和反向边,边数的两倍
vector<int> G[maxn];//邻接表,G[i][j]表示节点i的第j条边在edges数组中的序号
int a[maxn];//a[i]表示源点s到节点i的路径上的最小残留量
int p[maxn];//p[i]记录i的前驱,是用在edges数组里的序号表示的
void init(int n){
for(int i=0;i<=n;i++){
G[i].clear();
}
edges.clear();
}
void AddEdge(int from,int to,int cap){
edges.push_back(Edge(from,to,cap,0));
edges.push_back(Edge(to,from,0,0));//反向弧
int m=edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
int Maxflow(int s,int t){
int flow=0;
for(;;){
memset(a,0,sizeof(a));
queue<int> q;
q.push(s);
a[s]=INF;
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<G[x].size();i++){//x点对应的所有正向弧和反向弧
Edge& e=edges[G[x][i]];
if(!a[e.to]&&e.cap>e.flow){//当这个点没被访问过,且容量大于流量时
p[e.to]=G[x][i];
a[e.to]=min(a[x],e.cap-e.flow);
q.push(e.to);
}
}
if(a[t])break;//a[t]初始为0,若此处不为0说明找到了增广路了,break
}
if(!a[t])break;//如果找不到增广路,则当前流已经是最大流
for(int u=t;u!=s;u=edges[p[u]].from){
edges[p[u]].flow+=a[t];//更新正向流量
edges[p[u]^1].flow-=a[t];//更新反向流量
/*
异或运算,(^)向异为1,相同为0;
正向弧和反向弧保存在一起,eg、0,1;2,3…
一个数与1做异或运算,则其二进制除了最后一位,不变;
最后一位是1(奇数),则^1后为0,相当于值-1 (比如3对应2)
最后一位是0(偶数),则^1后为1,相当于值+1 (比如4对应5)
*/
}
flow+=a[t];//流加上
}
return flow;
}
int main(){
int x1,x2,x3;
while(scanf("%d%d",&E,&V)!=EOF){
S=1;
T=V;
init(V);
for(int i=0;i<E;i++){
scanf("%d%d%d",&x1,&x2,&x3);
AddEdge(x1,x2,x3);
}
printf("%d\n",Maxflow(S,T));
}
}
Dinic算法:
EK算法,每个阶段执行完一次bfs增广后,要重新启动bfs从源点寻找一条增广路,Dinic算法只需一个dfs就可实现多次增广,Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1。下面给出代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int MAX_V=205,INF=99999999;
int V,E,S,T;
struct edge{
int to,cap,rev;//终点、容量、反相边
};
vector<edge> G[MAX_V];//图的邻接表表示
int level[MAX_V];//顶点到源点的距离标号
int iter[MAX_V];//当前弧,在其之前的边已经没有用了
void init(int n){
for(int i=0;i<=n;i++){
G[i].clear();
}
}
void AddEdge(int from,int to,int cap){
G[from].push_back((edge){to,cap,int(G[to].size())});
G[to].push_back((edge){from,0,int(G[from].size())-1});
}
void bfs(int s){
memset(level,-1,sizeof(level));
queue<int> que;
level[s]=0;
que.push(s);
while(!que.empty()){
int v=que.front();que.pop();
for(int i=0;i<G[v].size();i++){
edge &e=G[v][i];
if(e.cap>0&&level[e.to]<0){
level[e.to]=level[v]+1;
que.push(e.to);
}
}
}
}
int dfs(int v,int t,int f){
if(v==t)return f;
for(int &i=iter[v];i<G[v].size();i++){
edge &e=G[v][i];
if(e.cap>0&&level[v]<level[e.to]){
int d=dfs(e.to,t,min(f,e.cap));
if(d>0){
e.cap-=d;
G[e.to][e.rev].cap+=d;
return d;
}
}
}
return 0;
}
int max_flow(int s,int t){
int flow=0;
for(;;){
bfs(s);
if(level[t]<0)return flow;
memset(iter,0,sizeof(iter));
int f;
while((f=dfs(s,t,INF))>0){
flow+=f;
}
}
}
int main(){
int x1,x2,x3;
while(scanf("%d%d",&E,&V)!=EOF){
S=1;
T=V;
init(V);
for(int i=0;i<E;i++){
scanf("%d%d%d",&x1,&x2,&x3);
AddEdge(x1,x2,x3);
}
printf("%d\n",max_flow(S,T));
}
}