第四章 支持向量机详解

1 线性可分模式的最优超平面

考虑训练样本${(x_i,d_i)}$假设由子集代表的模式是线性可分的，用于分离超平面的决策曲面方程是：

$$W^TX+b=0 \tag{式4.1}$$

其中x是输入向量，w是可调向量，b是偏置。因此可以写成：

$$W^TX+b\geq0 当 d_i=+1$$
$$W^TX+b<0 当d_i =-1\tag{式4.2}$$
支持向量机的目标是找到一个特殊的超平面，这个超平面分离边缘最大，在该情况下，决策曲面为最优超平面。假设 $w_0和b_0$分别表示权值向量和偏置的最优值，相应的，最优超平面形式如下：
$$w_0^T + b_0 = 0\tag{式4.3}$$
将式4.1改写，可得到判别函数：
$$g(x) = w_0^T+b_0\tag{式4.4}$$
x到最优超平面的距离是一种代数度量，可以将x表达为，（理解此处需要回顾高中几何、向量相关的知识，如下图所示那样）
$$x=x_0+r*\frac{ w_0}{ ||w_0||}$$

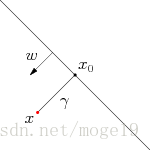
其中 $x_0$是x在最优超平面上的正轴投影，r是期望的代数距离。如果x在最优平面的正面，r是正值，相反，则为负值，由定义可知 $g(x_p)=0$,由此可得出：
$$g(x)=w_0^Tx+b_0=r||w_0||\tag{式4.5}$$
将超平面表示为（w,b),w为法向量，b为位移向，则样本空间到超平面（w,b）的距离可写为
$$r = \frac{|w^Tx+b|}{||w||}\tag{式4.6}$$
该步的解法详见（ https://blog.csdn.net/alwaystry/article/details/60957096）

假设超平面（w,b）能将训练样本正确分类，即$(x_i,y_i)\subset D$若$y_i=+1，则有w^Tx_i+b>0,y_i=-1,则有w^Tx_i+b<0$，令

$$\begin{cases} w^Tx_i+b\geq+1, & {y_i=+1} \\w^Tx_i+b\leq-1, & y_i =-1 \end{cases} \tag{式4.7}$$

由式4.6和式4.5可得出：

$$r =\frac{g(x)}{||w_0||}= \begin{cases} \frac{1}{||w_0||}, & {y_i=+1} \\-\frac{1}{||w_0||}, & y_i =-1 \end{cases} \tag{式4.8}$$
有式4.8可得到， 两个类边缘的最优值为 $\rho$:
$$\rho=2r = \frac{2}{||w_0||}\tag{式4.9}$$
由式4.9可以说明：
最大化两个类之间的边缘等价于最小权值向量w的欧几里得范数。
首先主要到训练样本{X,Y}，再根据式4.7，把两个等式合并得到一个等式：
$$y_i(w^Tx_i+b)\geq1$$
据此可总结，最大化两个类之间的分类边缘，即最大化间隔，仅需最大化 $||w||^{-1}$，等价于最小化 $||w||^2$(在《神经网络与机器学习》中，此处等价于 $w^Tw$)
于是可以得到如下：
$$min \frac{1}{2}||w||^2$$
$$y_i(w^Tx_i+b)\geq1,i=(1,2,\underbrace{\ldots}_{\rm ldots} ,N)$$
这就是支持向量的基本型。
在《神经网络与机器学习》中采用的记录方式为：
$$\Phi(w) = \frac{1}{2} w^Tw$$
$$y_i(w^Tx_i+b)\geq1,i=(1,2,\underbrace{\ldots}_{\rm ldots} ,N)\tag{式4.11}$$
代价函数 $\Phi(w)$是w的凸函数
约束条件关于w是线性的。
可以使用拉格朗日乘子方法解决约束最优问题。
首先，建立拉格朗日函数
$$J(w,b,a) = \frac{1}{2} w^Tw - \sum_{i=1}^n a_i[d_i(y_i(w^Tx_i+b)-1)]\tag{式4.12}$$

$a_i$称作拉格朗日乘子，约束最优问题的解由$J(w,b,a)$的鞍点决定，$J(w,b,a)$对w和b求微分并设置为0，得到两个最优条件：

$$\begin{cases}条件1：\frac{∂L(w,b,a)}{∂w} =0,\\条件2：\frac {∂L(w,b,a)}{∂b} =0 \end{cases}$$

应用最优条件1到式4.11的拉格朗日函数，得到：

$$w=\sum_{i=1}^N a_iy_ix_i\tag{式4.13}$$
同理运用最优条件2可得：
$$\sum_{i=1}^N a_iy_i=0\tag{式4.14}$$
KKT条件，（此处由式4.11，4.14得到)
$$\begin{cases}条件1：a_i\geq0\\条件2：y_if(x_i)-1\geq0\\条件3：a _i(y_if(x_i)-1)=0\end{cases} \tag{式4.15}$$
对偶问题
像前面提到的，原问题是处理凸代价函数和线性约束的，给定这样一个约束最优化问题，可能构造另一个问题，成为对偶问题。第二问题与原问题有同样的最优值，但是这是由拉格朗日乘子提供最优解。
为了说明对偶问题是原问题的前提，首先逐项展开式4.12如下：
$$J(w,b,a) = \frac{1}{2} w^Tw -\sum_{i=1}^Na_iy_iw^Tx_i - b \sum_{i=1}^Na_iy_i +\sum_{i=1}^Na_i \tag{式4.16}$$
根据式4.14，式4.16的右端第三项为零。由式4.13有
$$w^Tw = \sum_{i=1}^Na_iy_iw^Tx_i = \sum_{i=1}^N \sum_{j=1}^Na_ia_jy_iy_jx_i^Tx_j$$
相应地，设置目标函数 $J(w,b,a) = Q(a)$，可以将式4.16改写成:
$$Q(a) = \sum_{i=1}^Na_i - \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_ia_jy_iy_jx_i^Tx_j$$

现在可以将对偶问题做如下陈述：
给定训练样本$\tau = {(x_i,d_i)}$，寻找最大化如下目标函数的拉格朗日乘子$a_i$:

$$Q(a) = \sum_{i=1}^Na_i - \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_ia_jy_iy_jx_i^Tx_j$$
满足约束条件：
$$\sum_{i=1}^N a_iy_i=0$$
$$a_i\geq0，当i =1,2,3....,N时$$
可以用式4.13计算最优权值向量 $w_0$,并写成：
$$w_0=\sum_{i=1}^N a_0,iy_ix_i$$
运用式4.7，有：
$$b_0 = 1 - w_0^Tx^{(s)} = 1- \sum_{i=1}^Na_{o,i}d_ix_i^TX^{(s)}$$

[1]: 神经网络与机器学习 [加] Simmon Haykin