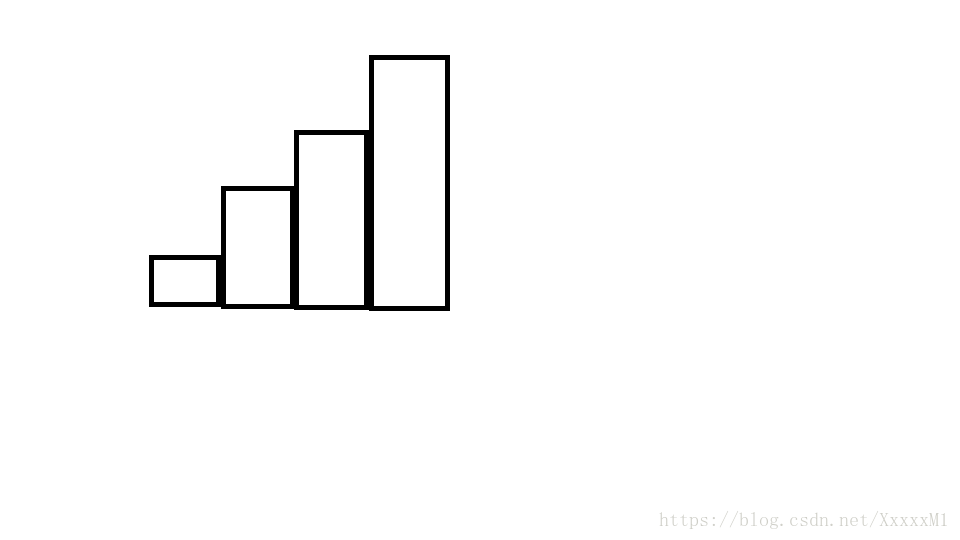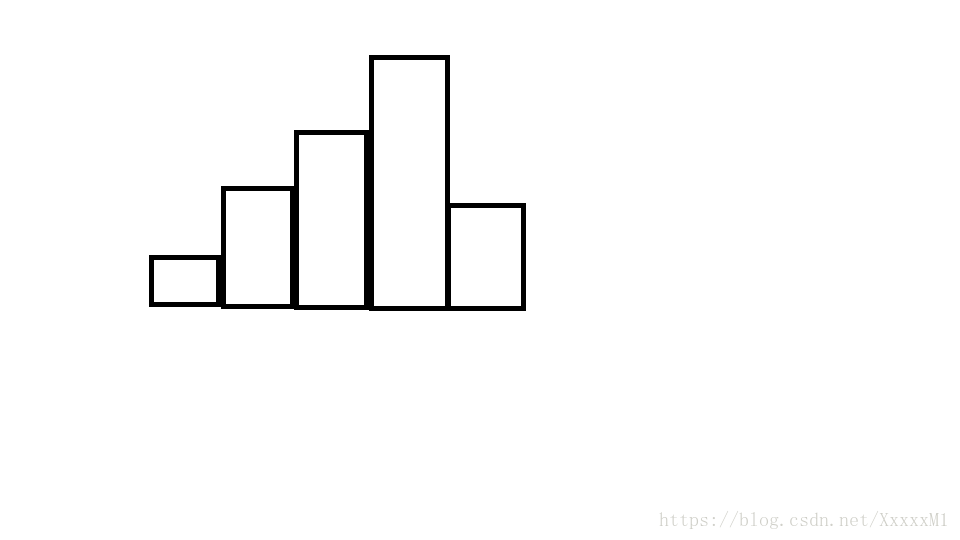问题描述
| 试题编号: | 201312-3 |
| 试题名称: | 最大的矩形 |
| 时间限制: | 1.0s |
| 内存限制: | 256.0MB |
| 问题描述: | 问题描述 在横轴上放了n个相邻的矩形,每个矩形的宽度是1,而第i(1 ≤ i ≤ n)个矩形的高度是hi。这n个矩形构成了一个直方图。例如,下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。 输入格式 第一行包含一个整数n,即矩形的数量(1 ≤ n ≤ 1000)。 输出格式 输出一行,包含一个整数,即给定直方图内的最大矩形的面积。 样例输入 6 样例输出 10 |
解题思路:
我们先来思考一个问题:如果矩形的高度从左到右单调递增,那么答案是多少?
显而易见,我们可以尝试以每个矩形的高度作为最终矩形的高度,并把宽度延伸到右边界,得到一个矩形,在所有的面积中取最大值就是答案。
如果下一个矩形的高度比上一个小,那么该矩形想利用之前的矩形一起构成一块较大面积时,这块面积的高度就不可能超过该矩形自己的高度。换句话说,在该矩形之前的矩形比其高的部分就没有丝毫用处了。
既然没有用处,那为什么不把比该矩形高的矩形都删掉,用一个宽度累加、高度为该矩形自己的高度的新矩形代替呢?这样并不会对后续计算产生影响。于是我们维护的轮廓就变成了一个高度始终递增的矩形序列,问题变得可解了。
详细地说,我们建立一个栈,用来保存若干个矩形,这些矩形的高度是单调递增的。我们从左到右依次扫描每一个矩形:
如果当前矩形比栈顶矩形高,直接进栈。
否则不断取出栈顶,直至栈为空或者栈顶矩形的高度比当前矩形小。在出栈过程中,我们累计被弹出的矩形的宽度之和,并且每弹出一个矩形,就用它的高度乘上累积的宽度更新答案。整个出栈过程结束后,我们把高度作为当前矩形的高度、宽度为累计值的新矩形入栈。
整个扫描结束后,我们把栈中剩余的矩形依次弹出,按照与上面相同的办法更新答案。为了简化程序实现,也可以增加一个高度为 0 的矩形 a [n+1] ,以避免在扫描结束后栈中有剩余矩形。
参考代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
while(cin>>n)
{
int a[1010],s[1010],w[1010],p=0;
long long ans=0;
memset(a,0,sizeof(a));
memset(s,0,sizeof(s));
memset(w,0,sizeof(w));
for(int i=1; i<=n; i++) cin>>a[i];
for(int i=1; i<=n+1; i++)
{
if(a[i]>s[p]) s[++p]=a[i],w[p]=1;
else
{
int width=0;
while(s[p]>a[i])
{
width+=w[p];
ans=max(ans,(long long)width*s[p]);
p--;
}
s[++p]=a[i],w[p]=width+1;
}
}
cout<<ans<<endl;
}
return 0;
}
这就是著名的单调栈算法,时间复杂度为 O(n)。借助单调性处理问题的思想在于即使排除不可能的选项,保持策略集合的高度有效性和秩序性,从而为我们做出决策提供更多的条件和可能方法。