背包问题学习总结

一、01背包问题

题目：有N件物品和一个容量为V的背包。放入第 i 件物品耗费的费用是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

就是存在两种状态：

第一种是第i件不放进去，这时所得价值为:f[i-1][v]

第二种是第i件放进去，这时所得价值为：f[i-1][v-c[i]]+w[i]

基本思路：最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态： F[ i,  v] = max{  F[ i - 1,  v],  F[ i - 1,  v - Ci] + Wi}

上面这个方程非常重要，基本所有跟背包相关的问题的方程都是由它衍生出来的。

解释一下上面的方程：“将前 i 件物品放入容量为 v 的背包中”这个子问题，若只考虑第 i 件物品的策略（放或不放），那么就可以转化为一个只和前 i - 1件物品相关的问题。如果不放第 i 件物品，那么问题就转化为“前 i - 1件物品放入容量为 v 的背包中”， 价值为F[ i - 1,  v ] ; 如果放第 i 件物品，那么问题就转化为“前 i - 1件物品放入剩下容量为v - Ci 的背包中”， 此时能获得的最大价值就是 F[ i - 1,  v - Ci] + Wi ；

代码： 

memset(F, 0, sizeof(F));
for(int i = 1; i <= n; i++)
   for(int j = Ci; j <= V; j++)
      F[i, v] = max(F[i - 1, v], F[i - 1, v - Ci] + Wi);

这样我们已经把基本的方程列出来了，下面就是优化了。。。。。

优化空间复杂度：

我们想能不能用一个F[ 0 .....v ]数组表示，下面我们进行了优化，这样 j 逆序就能够使后面F[v] -> F[ i - 1, v ]

和 F[v - Ci] -> F[ i - 1, v - Ci];

memset(F, 0, sizeof(F));
    for(int i = 1; i <= n; i++)
        for(int j = V; j <= Ci; j++)
        F[v] = max(F[v], F[v - Ci] + Wi);

最后就是初始化的细节问题。。。。。。

1、要求恰好装满背包：F[0] = 0,其他都是负无穷，这样能保证最终得到的F[ v ]是一种恰好装满背包的最优解。

2、没有要求必须装满：初始化时全部设为0。

二、完全背包问题

题目：有N种物品和一个容量为V的背包，每种背包都有无限件可用。放入第 i 种物品的费用是Ci ，价值是Wi。

求解：将哪些物品装入背包，可使这些物品的耗费的费用总和不超过背包容量，且价值总和最大。

 基本思路：这个问题非常类似于01背包问题，所不同的是每种物品有无限件。也就是从每种物品的角度考虑，与它相关的策略已并非取或不取两种，而是有取0件、取1件、。。。。直至取V/Ci件等许多种。

如果仍然按照解01背包时的思路，令F[i, v] 表示前i种物品恰好放入一个容器为V的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程：

F[ i , v ] = max{ F[ i - 1, v - kCi]+ kWi |0 <= kCi <= v|};

这个可以使用一维数组实现：

for(int i = 1; i < n; i++)
   for(int j = Ci; j <= V; j++)
      F[j] = max(F[v], F[v - Ci] + Wi);

这样子刚好内层循环与01背包的内存循环顺序相反。。。

我们来讨论一下为什么上面这个算法可行。。

首先01背包，我们定义v->Ci,是因为我们需要保证F[ i, v] 是由状态F[ i - 1, v - Ci]递推而来，至于为什么需要这个样子做，上面已经提到，每种物品只能取一件；然而完全背包则可以取无限件， 那我们就需要考虑“我们加入一件第i种物品”这个策略时，我们可能恰恰需要可能已经选入第 i 件的商品的子结果F[i , v - Ci]，所以就可以采用v递增的顺序循环。

三、多重背包问题

 有N种物品和一个容量为V的背包。第 i 种物品最多有Mi件可用，每件耗费的空间是Ci，价值是Wi。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

基本思路：多重背包问题与完全背包问题类似，对于第i种物品有n[i] + 1种策略，即取0件、取1件、......、取n[i]件，用F[i, v]表示前i件物品恰好装满背包V的最大价值，由此我们得出状态转移方程：

F[ i , v] = max( F[i - 1][v - k*Ci] + k*wi)(0<=k<=n[i])

这样复杂度是O(Vni).....

代码是这样子的：

#include<bits./stdc++.h>

using namespace std;
const int maxn = 10;
int V, n[maxn], weight[maxn], dp[maxn][maxn], C[maxn];

int multipack()
{
	memset(dp, 0, sizeof(dp));
	for(int i = 0; i < maxn; i++)
	{
		for(int v = C[i]; v <= V; v++)
		{
			dp[i][v] = 0;		
			int ncount = min(n[i], v/C[i]);
			for(int k = 0; k < ncount; k++)
			{
				dp[i][v] = max(dp[i][v], dp[i  - 1][v - k*C[i]] + k*weight[i]);	
			}			
		}
	}
	return dp[maxn][V];
}

然而等到ni很大的时候，我们不得不选择另一种复杂度为O(Vlog(ni)).....

我们考虑二进制的思想，我们考虑把第i件物品换成若干件物品，其中每件物品都有一个系数。这件物品的价值和费用均是原来的价值和费用乘以这个系数令这些系数分别是1,2,....,  ,n[i] - + 1;且k满足n[i] - + 1 > 0的最大整数。。。

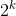
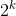
注意，

（1）最后一个物品的件数的求法和前面不同，其直接等于 该物品的最大件数 - 前面已经分配之和。

（2）分成的这几件物品的系数和为Num[i]，表明第i种物品取的件数不能多于Num[i]。

举例：某物品为13件，则其可以分成四件物品，其系数为1,2,4,6.这里k = 3。

当然，这里使用二进制的前提还是使用二进制拆分能保证对于0,,,Num[i]间的每一个整数，均可以用若干个系数的和表示。

具体使用时，有一个小优化，即：

我们不对所有的物品进行拆分，因此物品一旦拆分，其物品个数肯定增加，那么复杂度肯定上去。

此时，我们可以选择性地对物品进行拆分：

（1）如果第i个物品的重量Weight[i] * 物品的个数Num[i] >= 背包总重量V，可以不用拆分。

（2）如果第i个物品的重量Weight[i] * 物品的个数Num[i] < 背包总重量V，需要拆分。

其实，拆不拆分，就看该物品能不能满足完全背包的条件。即，看该物品能不能无限量供应。

解释：为啥满足Weight[i] * 物品的个数Num[i] >= 背包总重量V的物品可以不用拆分?

此时，满足该条件时，此物品原则上是无限供应，直到背包放不下为止。

最终，对于不需要拆分的物品，可以看出完全背包的情况，调用处理完全背包物品的函数。对于需要拆分的物品，可以看出01背包的情况，调用处理01背包物品的函数。

这样，由于不对满足完全背包的物品进行拆分，此时物品个数就没有对所有物品拆分时的物品个数多，即程序中外层循环降低，复杂度也就下去了。

伪代码：

这里：C表示该物品的重量。M表示该物品的个数。V表示背包的最大容量。W表示该物品的收益。

代码：

#include <iostream>
using namespace std;

const int N = 3;//物品个数
const int V = 8;//背包容量
int Weight[N + 1] = {0,1,2,2};
int Value[N + 1] = {0,6,10,20};
int Num[N + 1] = {0,10,5,2};

int f[V + 1] = {0};
/*
f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。
f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
v的为逆序
*/
void ZeroOnePack(int nWeight,int nValue)
{
	for (int v = V;v >= nWeight;v--)
	{
		f[v] = max(f[v],f[v - nWeight] + nValue);
	}
}

/*
f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。
f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
v的为增序
*/
void CompletePack(int nWeight,int nValue)
{
	for (int v = nWeight;v <= V;v++)
	{
		f[v] = max(f[v],f[v - nWeight] + nValue);
	}
}

int MultiKnapsack()
{
	int k = 1;
	int nCount = 0;
	for (int i = 1;i <= N;i++)
	{
		if (Weight[i] * Num[i] >= V)
		{
			//完全背包:该类物品原则上是无限供应，
			//此时满足条件Weight[i] * Num[i] >= V时，
			//表示无限量供应，直到背包放不下为止.
			CompletePack(Weight[i],Value[i]);
		}
		else
		{
			k = 1;
			nCount = Num[i];
			while(k <= nCount)
			{
				ZeroOnePack(k * Weight[i],k * Value[i]);
				nCount -= k;
				k *= 2;
			}
			ZeroOnePack(nCount * Weight[i],nCount * Value[i]);
		}
	}
	return f[V];
}

int main()
{
	cout<<MultiKnapsack()<<endl;
	system("pause");
	return 1;
}

四、混合背包