1、蒙特卡洛方法概述
蒙特卡罗原来是一个赌场的名称,用它作为名字大概是因为蒙特卡罗方法是一种随机模拟的方法,这很像赌博场里面的扔骰子的过程。最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分:
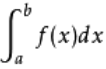
如果此时f(x)很难求出其原函数时,那么这个积分就非常难求。当然我们可以通过蒙特卡洛方法来模拟求解近似值,假设我们的函数f(x)如下图所示
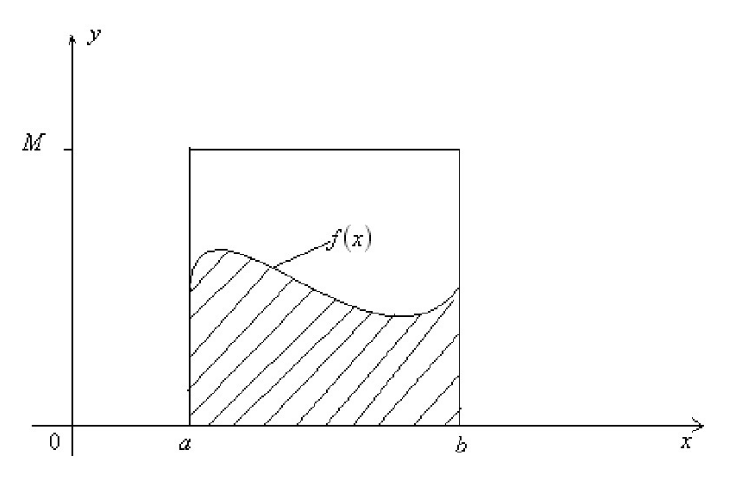
则一个简单的近似求解方法是在[a,b]之间随机的采样一个点。比如x0,然后用f(x0)代表在[a,b]区间上所有的f(x)的值。那么上面的定积分的近似求解为:
(b−a)f(x0)
然而上面的式子太过于简单,近似出来的误差较大,我们将其分成n等分,则近似解可以表示为
[(b−a)/n] [f(x0) + f(x1) + ... + f(xn-1)]
然而上面改进的式子是在假设x在[a,b]之间是均匀分布的前提下的,而绝大部分情况,都是非均匀分布的,甚至有的是离散的值,因此提出了蒙特卡洛积分法:
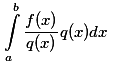
则近似解可以表示为
1/n [f(x0)/p(x0) + f(x1)/p(x1) + ... + f(xn-1)/p(xn-1)]
2、概率分布采样
上一节我们讲到蒙特卡罗方法的关键是得到x的概率分布。如果求出了x的概率分布,我们可以基于概率分布去采样基于这个概率分布的n个x的样本集,代入蒙特卡洛近似求解式子中。但是还有一个关键的问题需要解决,即如何基于概率分布去采样基于这个概率分布的n个x的样本集。
对于常见的均匀分布uniform(0,1)是非常容易采样样本的,一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布,无论是离散的分布还是连续的分布,它们的样本都可以通过uniform(0,1)的样本转换而得。比如二维正态分布的样本(Z1,Z2)可以通过通过独立采样得到的uniform(0,1)样本对(U1,U2)通过如下的式子转换而得:
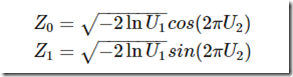
除了正态分布之外,还有很多其他常见的连续分布也可以用均匀0-1分布来表示,不过很多时候我们的分布并不是常见的分布,这也就以为着无法通过这些转换来获得样本集的概率分布。
3、接受-拒绝采样
对于概率分布不是常见的分布,一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 p(x) 太复杂在程序中没法直接采样,那么我设定一个程序可采样的分布 q(x) 比如高斯分布,然后按照一定的方法拒绝某些样本,以达到接近 p(x) 分布的目的,其中q(x)叫做 proposal distribution。
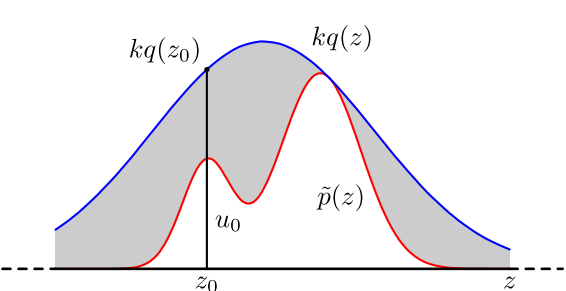
具体操作如下,设定一个方便抽样的函数 q(x),以及一个常量 k,使得 p(x) 总在 kq(x) 的下方。(参考上图)
1)x 轴方向:从 q(x) 分布抽样得到 a。
2)y 轴方向:从均匀分布(0,kq(a)) 中抽样得到 u。
3)如果刚好落到灰色区域: u > p(a),拒绝, 否则接受这次抽样。
4)重复以上过程。
4、小结
使用接受-拒绝采样,我们可以解决一些概率分布不是常见的分布的时候,得到其采样集并用蒙特卡罗方法求和的目的。但是接受-拒绝采样也只能部分满足我们的需求,在很多时候我们还是很难得到我们的概率分布的样本集。比如:
1)对于一些二维分布p(x,y),有时候我们只能得到条件分布p(x|y)和p(y|x)和,却很难得到二维分布p(x,y)一般形式,这时我们无法用接受-拒绝采样得到其样本集。
2)对于一些高维的复杂非常见分布p(x1,x2,...,xn),我们要找到一个合适的q(x)和k非常困难。