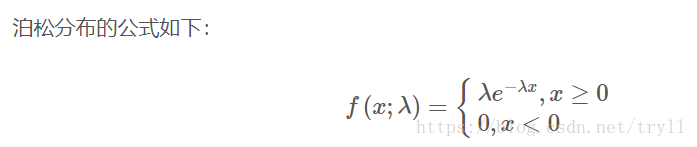1、随机变量的定义:
在一次实验中出现的所以结果次数M,将每一种结果映射到某种数值函数X(e)(e表示是某一次实验发生的结果),这种命映射的结果值称为随机变量。
2、随机变量分为离散型和连续型的。
3、分布律:只有离散型随机变量具有分布律,例如:离散型随机变量的x的分布律师0,1,2; 分别对应的概率是0.3, 0.4, 0.3。
4、分布函数:该概念对于离散型和连续型都是适用的。F(x)=p{X<=x},则F(x)叫做随机变量X的分布函数(注意大写X,小写x的区别。)
5:连续型的分布律的定义:再有了分布函数的基础上面,我们在来定义分布律;如下图
则X成为连续型随机变量,f(x)称为密度函数。这个可以类比离散型的分布律。
下面介绍一下常见的各种分布;
1、01分布
对于01分布,随机变量只有两种,而且实验只是进行了一下。

2、伯努利分布
相对于01分布,随机变量两种,但是实验室重复了N次。
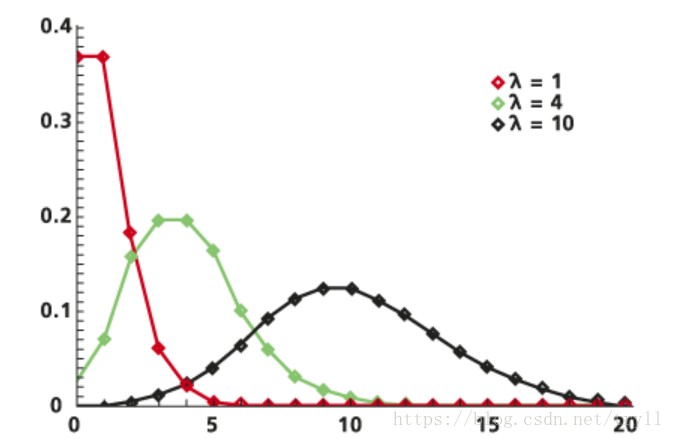
3、泊松分布:
泊松分布适合在给定一个已知平均值的情况下对固定时间步长内事件的发生次数概率进行建模。这些事件与它们最后一次发生的状态无关。X 轴上是 0、1、2、3、4(以此类推)等事件的离散值(通常表示事件的发生次数),Y 轴上是现象的发生概率(通常是给定一个已知平均值)。这些事件可以是十字路口的事故发生次数、出生缺陷数量或一平方公里内驼鹿的数量。泊松分布可以对小概率事件进行建模。这种分布有时也被称为小数定律 (Law of small numbers),因为事件不经常发生,但仍有很多机会让它发生。
其中的参数说明: x表示的是事件可能发生的次数(正整数);
λ是一个平均值,表示在一定区间内事件预计发生的次数,
泊松分布与二项分布类似,但泊松分布是在不知道事件的可能发生总次数的情况下对小概率事件建模。泊松分布的建模对象是十字路口的事故发生次数,而二项分布的建模对象是事故发生次数与经由十字路口的汽车数量之间的相对关系。
期望值:λ(即,平均值)
方差:方差σ²与均数λ相等,即σ²=λ
以上博客参考了:http://hongyitong.github.io/2016/11/13/%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83%E3%80%81%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83%E3%80%81%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/
poisson分布的性质:
1、poisson分布是单参数你的离散型分布,其中参数λ表示的是在时间或者空间上面某事件发生的平均次数。
2、poisson的方差和均值都是λ。
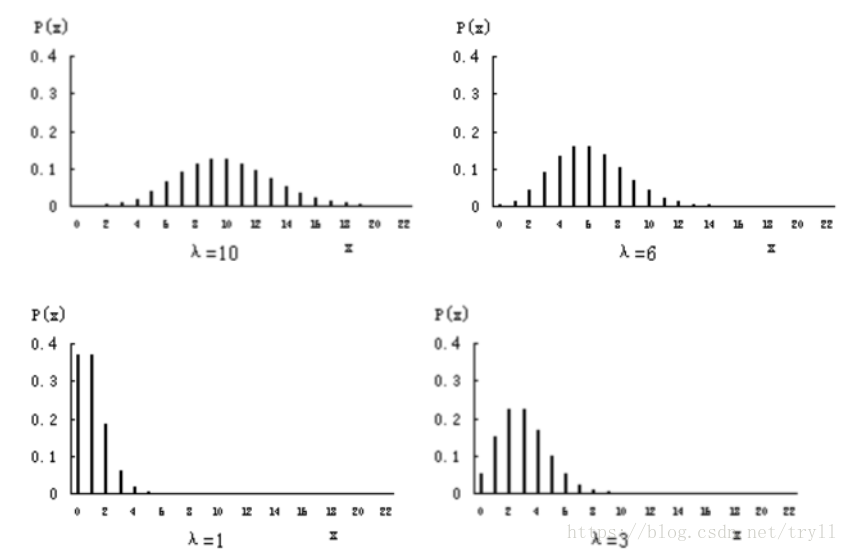
3、poisson是非对称的分布,在λ不大时呈偏态分布,随着λ的增大,迅速接近正态分布。一般来说,当λ=20时,可以认为近似正态分布,Poisson分布资料可按正态分布处理。
4、poissson的累计概率有左侧累计和右侧累计。
上图是关于λ取到不同的数值,对应的分布图,可以看出随着λ增大,越来越接近正太分布,一般在实际处理的时候会利用近似正太分布来处理。
二项分布:二项分布是指在一些潜在事件观测对事件的发生次数建模。例如,二项分布可用于采集在临床研究中死于心脏病的人数、拥挤电梯中在第二层走出电梯的人数,或是某动物种群中携带特定遗传性状的动物数量。
二项分布描述的是发生次数,而不是量值。它可以对完成比赛的参赛者数量建模,但不能对参赛者的速度建模。
其中的参数说明:n代表的是观测值的数量;p发生的概率;x代表的是成功的次数。
使用二项分布的一个常见例子是,在抛掷硬币 10 次 (n = 10) 的情况下判断硬币正面朝上的次数概率。可能出现的情况是,10 次中有 0 次正面朝上、10 次中有 1 次正面朝上,以此类推;因此,x = 0、1、2、3、4、5、6、7、8、9、10。p 是每个 x 的概率。
所有试验都是相互独立的,并且每个试验只有成功和失败这两种结果。
如果 n 值较大且 p 值较小,则二项分布接近泊松分布。这种情况下使用泊松分布会更加简便。
二项分布将返回代表 n 次试验中成功次数的随机变量,其中每次试验的成功概率为 p(例如,硬币正面朝上的概率为 p)。
从二项分布中获得 :
期望值: μ=np
方差: σ²=np(1-p)
2、连续型随机变量的常见分布:
(1)、均匀分布
(2)、指数分布
(3)、正太分布:它的理论基础是中心极限定理,该定理的原理是:如果存在大量观测值,则随机变量的总和将呈正态分布。例如,如果多次抛掷硬币,则在一连串抛币动作中硬币正面朝上的次数将接近正态分布。正态分布的例子包括:某国家的人的身高、某个省的各个高程值以及 12 岁学生的数学考试分数。
其中参数:μ代表的是平均值
σ标准差(正数)正态分布关于平均值、众数和中值对称(都在 μ 处相等)。
通常二项分布和泊松分布使用数量较少的观测值对未来的离散型独立随机事件(可能发生,也可能不发生。例如,抛硬币时硬币正面朝上的次数)建模,而正态分布则使用大量的观测值对连续型变量(例如高度、重量和金额)建模。二项分布和泊松分布以概率为基础,而正态分布涉及的是达到某个量或量值的观测值数量。