数据结构图总结

图

1.图的术语与定义

1.1图的定义

顶点 $i$ 的出度：第 $i$ 行1的个数。顶点 $i$ 的入度，第 $i$ 列1的个数。

图由顶点集V(G)和边集E(G)组成，记为G=(V,E)。其中E(G)是边的有限集合，边是顶点的无序对（无向图）或有序对（有向图）。

对有向图来说，E(G)是有向边（也称弧(Arc)）的有限集合，弧是顶点的有序对，记为 $<v, w>$ ，v、w是顶点，v为弧尾（箭头根部），w为弧头（箭头处）。

对无向图来说，E(G)是边的有限集合，边是顶点的无序对，记为(v, w)或者(w, v)，并且(v, w)=(w,v)。

1.2顶点的度、入度、出度

顶点v的度：与v相关联的边的数目；

顶点v的出度：以v为起点有向边数；

顶点v的入度：以v为终点有向边数。

1.3路径与回路

简单路径：序列中顶点不重复出现的路径

简单回路：序列中第一个顶点和最后一个顶点相同的路径

1.4连通图（强连通图）

在无（有）向图中，若对任何两个顶点v、u都存在从v到u的路径，则称图G为连通图（强联通图）。

极大连通子图：该子图是G连通子图，将G的任何不在该子图的顶点加入，子图将不再连通。

极小连通子图：该子图是G的连通子图，在该子图中删除任何一条边，子图都将不再连通。

无向图G的极大连通子图称为G的连通分量。

有向图D的极大强连通子图称为D的强连通分量。

包含无向图G的所有顶点的极小连通子图称为G**生成树**。

若T是G的生成树当且仅当T满足：T是G的连通子图、T包含G的所有顶点、T中无回路。

2.图的存储

2.1邻接矩阵

顶点 $i$ 的出度：第 $i$ 行1的个数。顶点 $i$ 的入度，第 $i$ 列1的个数。

typedef enum {DG, DN, UNG, UDN} GraphKind;//有向图，有向网，无向图，无向网
typedef struct ArcCell {
    VRType adj;//无权图，用0,1表示；带权图，用权值类型表示
    InfoType *info;//弧相关信息的指针
}ArcCell, AdjMatrix[maxn][maxn];
typedef struct {
    VertexType vexs[maxn];//顶点信息
    AdjMatrix arcs;//建立邻接矩阵
    int vexnum, arcnum;//图的当前顶点数和弧数
    GraphKind kind;
}MGraph;

2.2邻接表

无向图的邻接表

typedef struct ArcNode {//一般结点
    int adjvex;//该弧所指向的顶点的位置
    struct ArcNode *nextarc;//链域，指向下一条边或者弧
}ArcNode;
typedef struct tnode{//表头结点
    int vexdata;//存放顶点信息
    ArcNode *firstarc;//指向第一个邻接点
}VNode, ADjList[maxn];
typedef struct{//最终建立邻接表
    ADjList vertices;
    int vexnum, arcnum;
    int kind;
}ALGraph;

无向图采用邻接表存储的特点：

在G连接表中，同一条边对应两个结点。顶点v的度，等于 v对应线性链表的长度。在G中增减边，需要在两个单链表中插入、删除结点。

设存储顶点的一维数组大小为 $m$ ( $顶点数m>顶点数n$ )，图的边数为 $e$ ，则图G占用存储空间大小为 $m+2*e$ 。适用于边稀疏的图。

有向图的邻接表

有向图的邻接表：以同一顶点作为起点的弧。出边表。 $e$ 个边结点。

有向图的逆邻接表：以同一顶点作为终点的弧。入边表。 $e$ 个边结点。

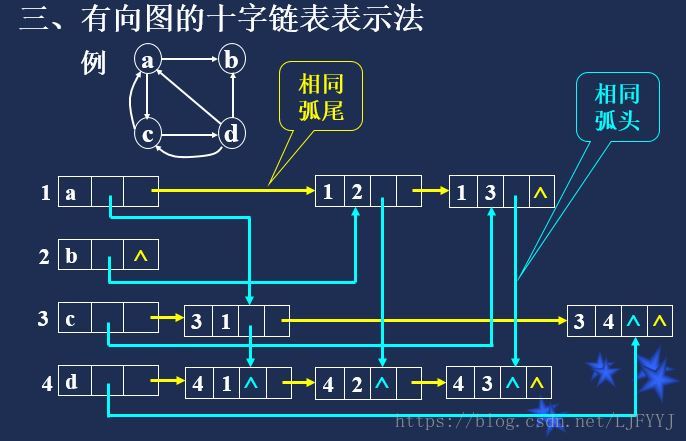
2.3有向图的十字链表表示法

typedef struct ArcBox{//建立弧结点
    int tailvex, headvex;//弧头、弧尾在表头数组中位置
    struct arcnode *hlink;//指向弧头相同的下一条弧
    struct arcnode *tlink;//指向弧尾相同的下一条弧
}ArcBox;
typedef struct VexNode{//顶点结点
    VertexType data;
    ArcBox *firstin;//指向以该顶点为弧头的第1个弧结点
    ArcBox *firstout;//指向以该顶点为弧尾的第1个弧结点
}VexNode;
VexNode OLGraph[M];

之前的邻接表都是弧尾相同，弧尾即箭头根部。
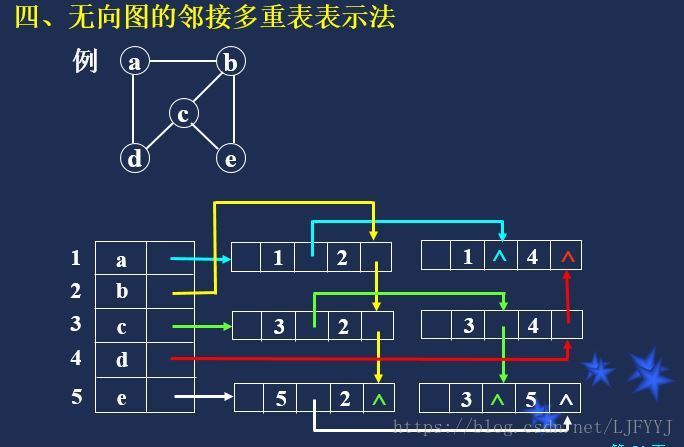
这里写图片描述

2.4无向图的邻接多重链表表示法

注意一下与上图的差别，在于顶点结点的指针数量。

typedef struct node {//弧结点
    VisitIf mark;//标志域，记录是否已经搜索过
    int ivex, ijex;//该边依附的两个顶点在表头数组中位置
    struct EBox *ilink, *jlink;//分别指向依附于ivex和ijex的下一条边
}EBox;
typedef struct VexBox{//顶点结点
    VertexType data;//存与顶点有关的信息
    EBox *firstedge;//指向第一条依附于该顶点的边
} VexBox;
VexBox AMLGraph[M];

这里写图片描述

3.图的遍历

3.1深度优先遍历（Depth First Search)

从图的某顶点v出发，进行深度优先遍历：

访问顶点v
对于v的所有邻接点 $w_1、w_2、w_3…$ ，若 $w_i$ 没有被访问，则从 $w_i$ 出发进行深度优先遍历。

由于没有规定访问邻接点的顺序，所以深度优先序列不唯一。

void DFSTraverse(Graph G, void(*visit)(VertexType e))//对G做深度优先遍历
{
    for(v = 0; v < G.vexnum; v++)
        visited[v] = flase;
    for(v = 0; v < G.vexnum; v++){
        //注意：若图为非连通图，只有这样才能完全深度优先遍历;若为连通图，则可以用一个DFS函数
        if(!visited[v])
            DFS(G, v, Visit);
    }
}
void DFS(Graph G, int v, void(*Visit)(VertexType e))//对每个顶点做深度优先遍历
{
    visited[v] = true;
    Visit(v);
    for(w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)){
        if(!visited[w])
            DFS(G, w, Visit);
    }
}

时间复杂度：

若图为邻接表表示为 $O(n+e)$ ，若为邻接矩阵表示为 $O(n+n^2)=O(n^2)$ 。

3.2广度优先遍历(Breadth First Search)

从图中某顶点v出发：

访问顶点v
访问顶点v所有未被访问的邻接点 $、w_1、w_2…w_n$ ，并用栈或队列存储
依次取出邻接点进行广度优先遍历

深度优先遍历是回溯算法，广度优先遍历时一种分层的顺序搜索过程，不是递归。

void BFSTraverse(Graph G, void(*visit)(VertexType))//对G做广度优先遍历
{
    for(v = 0; v < G.vexnum; v++)
        visited[v] = false;
    for(v = 0; v < G.vexnum; v++){
        if(!visited[v])
            BFS(G, v, Visit);
    }
}
void BFS(Graph G, int v, void(*Visit)(VertexType e))
{
    initqueue(Q);//在把每一个结点放到队列中前，先把它标记和处理
    visited[v] = true;
    Visit(v);
    push(v);
    while(!empty(Q)){
        v = pop(Q);
        for(w = FirstAdjvex(G, v); w >= 0; w = NextAdjvex(G, v, w)){
            if(!visited[w]){
                visited[w] = true;
                Visit(w);
                push(w);
            }
        }
    }  
}

3.3遍历的应用

求一条从顶点v到顶点s的简单路径

方法：从v开始深度优先遍历，直到找到s。在对v深度优先遍历的过程中，首先将v添加到路径中，判断v的值是否为s，如果为s，返回真。如果不为s，则对v的邻接点进行递归，直到找到s为止。如果没找到，则将v从路径中删除，返回失败。

Status _DFSearch(Graph G, int v, VertexType s, SqList &Path)//递归函数
{
    visited[v] = true;
    ListAppend(v, Path);//将v添加到路径中
    for(w = FirstAdjvex(G, v); w >= 0; w = NextAdjvex(G, v, w)){//判断是否有路
        if(!visited[w]){
            if(_DFSearch(G, w, s, Path)) return true;
        }
    }
    ListDelete(v, Path);//将v从路径中删除
    return False;
}

求两个顶点之间的一条路径长度最短的路径

由于广度优先搜索有路径渐增的性质，所以使用广度优先搜索，搜索到终点的路径即为最短路径。应该会需要用一个数组记录每个节点的父节点，便于还原路径。

4.图的最小生成树

4.1最小生成树的概念

包含无向连通图G所有n个顶点的极小连通子图称为G的生成树。

生成树的特点：T是G的连通子图；T包含G的所有顶点；T中无回路；T中有n-1条边。

权之和最小的生成树为最小生成树。

MST(Minimum Spanning Tree)性质： 若U集是V的一个非空子集，若( $U_0$ , $V_0$ )是一条权值最小的边，其中 $U_0\in U$ , $V_0\in V-U$ ，则：( $U_0$ , $V_0$ )必在最小生成树上。

4.2 Prim算法：将顶点归并，与边数无关，适合稠密网 $O(n^2)$

设G=(V,GE)为一个具有n个顶点的连通网络，T=(U,TE)为构造的生成树。

初始时，U={ $u_0$ }，TE为空集
在所有的 $u\in U$ 且 $v\in V-U$ 的边(u,v)中选择一条权值最小的边(u,v)
将(u,v)加入TE，同时将v加入U
重复23步，直到U=V为止

//辅助数组closege[]，对当前V-U集中的每个顶点，记录与顶点集U中顶点相连接的代价最小的边。
struct{
    VertexType Adjvex;//顶点v到子集U中权最小边关联的顶点u
    VRType lowcost;//顶点v到子集U中权最小边的权值
}closedge[maxn];
void MiniSpanTree_P(MGraph G, VertexType u)//从u出发构造G的最小生成树
{
    k = LocateVex(G, u);
    for(j = 0; j < G.vexnum; ++j){//辅助数组初始化
        if(j != k)
            closedge[j] = {u, G.arcs[k][j]};//各点到u的距离
    }
    for(i = 0; i < G.vexnum; i++){
        k = minimum(closedge);//选择距离最小且不为0的作为k
        printf(closedge[k].Adjvex, G.vexs[k]);//输出k对应的顶点和新加入的边权值
        closedge[k].lowcost = 0;//加入新的点
        for(j = 0; j < G.vexnum; j++){
            if(G.arcs[k][j] < closedge[j].lowcost)//更新V-U中点到U中点的距离
                closedge[j] = {G.vexs[k], G.arcs[k][j]}；
        }
    }
}

4.3 Kruskal算法：将边归并，适用于求稀疏网的最小生成树 $O(eloge)$

初始时最小生成树值包含图的n个顶点，每个顶点为一棵子树
选取权值较小且所关联的两个顶点不再同一连通分量的边，将此边加入最小生成树中
重复第二步n-1次，即得到包含n个顶点和n-1个条边的最小生成树

int find(int n)//找到点的树根
{
    while(n != find[n])
        n = find[n];
    return n;
}
void join(int n, int m)//将两棵树并起来
{
    int fn = find(n);//一定要找到两棵树的树根再并到一起
    int fm = find(m);
    find[fn] = fm;
}
int kruskal(int n, int m)
{
    int num = 0;
    for(i = 1; i <= n; i++)//初始化寻根函数
        find[i] = i;
    for(i = 0; i < m; i++){//此时A中边已经全部从小到大排好顺序
        if(find(A[i].u) != find(A[i].v)){//如果边的顶点不属于一棵树
            join(u, v);//并到一棵树
            cost += A[i].w;
            num++;//通过最后num是否达到n-1来判断是否有最小生成树
        }
    }
}

5.有向无环图及其应用

对于有向图中没有限定次序关系的顶点，则可以人为加上任意的次序关系，由此所得顶点的线型序列被称之为拓扑有序序列。

AOV网(Activity On Vertex network)是以顶点表示活动，弧表示活动之间的先后关系的有向图。AOV网中不允许有回路，不允许某项活动以自己为先决条件。

检测AOV网是否存在环：对有向图构造顶点的拓扑有序序列，若图中所有顶点都在该序列中，则AOV网必定不存在环。

AOE网(Activity On Edge)用边表示活动的网。它是一个带权的有向无环图。

AOE网中重要概念：

顶点表示时间，弧表示活动
权值：活动持续的时间
路径长度：路径上各活动的持续时间之和
关键路径：路径长度最长的路径叫作关键路径
关键活动：该弧上的权值增加将使有向图上的最长路径的长度增加

AOE网和AOV网的区别：

一个用顶点表示活动，一个用边表示活动
AOV网侧重表示活动的前后次序，AOE网除了表示活动的前后次序，还表示了活动的持续时间等。

AOV网或AOE网构造拓扑序列的方法：

在有向图中选一个没有前驱（入度为0）的顶点并输出它。
从图中删除该顶点和所有以它为尾的弧。（弧头顶点的入度减一）
重复上述两步，直至全部顶点均已输出。

数据结构：

邻接表存储图
数组记录顶点当前的入度
栈记录入度为0的点

6.最短路径

6.1 Dijkstra算法求单源最短路径

方法： $S={v_0}$ ， $其余顶点T={其余顶点u}$

从T中选择一个未标记的权值最小的顶点w，将w加入S，并对w进行标记。若所有点都被标记，则结束。
考察T中的所有顶点，对路径进行松弛

void SPath_Dij(MGraph G, int u0, int dis[], int Path[])
{
    for(i = 0; i < G.vexnum; i++){
        visited[i] = flase;
        dis[i] = G.arcs[u0][i];
        if(dis[i] < INFINITY) Path[i] = u0;//path用来记住前一个结点
        else Path[i] = -1;
    }
    dis[u0] = 0; visited[u0] = true;
    for(i = 0; i < G.vexnum; i++){
        k = selectmin(dis);
        visited[k] = true;//注意k此处应该被标记
        for(j = 0; j < G.vexnum; j++){
            if(dis[j] > dis[k] + G.arcs[k][j] && !visited[j]){
                //选出的j不应该被访问过
                dis[j] = dis[k] + G.arcs[k][j];
                Path[j] = k;//注意对Path进行更新
            }
        }
    }
}

无向图和有向图都适用，弧的权值必须非负。

6.2 Floyd算法求每对顶点间最短路径

当然也可以重复执行Dijkstra算法n次。

弗洛伊德算法：从 $v_i$ 到 $v_j$ 所有可能存在的路径中，选出一条长度最短的路径。

方法：

初始设置一个n阶方阵，令其对角线元素为0，若存在弧 $<v_i, v_j>$ ，则对应元素为权值，否则为无穷。
逐步试着在原直接路径中增加中间顶点，若加入中间点后路径变短，则修改。否则，维持原值。
所有顶点试探完毕，算法结束。

//核心算法类似于动态规划
for(i = 0; i < G.vertex; i++){
    for(j = 0; j < G.vertex; j++){
        for(k = 0; k < G.vertex; k++){
            if(A[i][j] > A[i][k] + A[k][j]){
                A[i][j] = A[i][k] + A[k][j];
                path[i][j] = k;//记录分段点
            }
        }
    }
}

图