好题杂题

$T_1$

题目大意【gdoi2018 day2】第二题滑稽子图（subgraph）

给你一颗树$T$，以及一个常数$K$，对于$T$的点集$V$的子集$S$.
定义$f(S)$为点集$S$的导出子图的边数（一条原树中的边只有两个端点都出现在$S$中，才会出现在导出子图中）

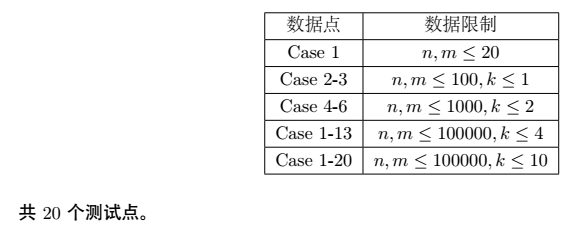
数据范围

这里写图片描述

解题方案

$Part_1$ 5%

随便做

$Part_2$ 30%

考虑一下DP.
设$f[i][j][0/1]$表示第$i$个点，导出子图边数为$j$，第$i$个点是否选.
转移讨论一下即可，这里需要注意一下转移时用顺推还是逆推.
一般来说，对于背包类型的，我们顺推可以使每一个转移都是有效的.
枚举之前子树大小和，以及当前子树大小，乘积的和是$O(n^2)$级别的.
证明：
- 两个点会产生贡献，当且仅当它们的$LCA$为当前的根时，每两个点的$LCA$唯一，故只有$O(n^2)$个点会产生贡献.

$Part_3$ 100% DP

依然是DP，但我们要利用好$k\le 10$这个特性.
我们来观察一下顺推时的转移，其实可以表示为：
- 令当前计算的是$y$对于父亲$x$的贡献，表达如下：
  \[f[x][i + j] = \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * (i + j) ^ k \]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{i = 0}^{size_x - 1}\sum_{j = 0}^{size_y - 1} f[x][i]*f[y][j] * \sum_{t = 0}^ki^t*j^{k-t}*\binom{k}{t}\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{i = 0}^{size_x - 1}\sum_{j = 0}^{size_y - 1} \sum_{t = 0}^k\binom{k}{t}f[x][i]*f[y][j] *i^t*j^{k-t}\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{i = 0}^{size_x - 1}\sum_{j = 0}^{size_y - 1} \sum_{t = 0}^k\binom{k}{t}(f[x][i]*i^t) (f[y][j]*j^{k-t})\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{t = 0}^k\binom{k}{t}\sum_{i = 0}^{size_x - 1}\sum_{j = 0}^{size_y - 1} (f[x][i]*i^t) (f[y][j]*j^{k-t})\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{t = 0}^k\binom{k}{t}\sum_{i = 0}^{size_x - 1} (f[x][i]*i^t)\sum_{j = 0}^{size_y - 1} (f[y][j]*j^{k-t})\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[令g[x][t]表示\sum_{i = 0}^{size_x-1}f[x][i]*i^t，则上式转化为\]
  $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
  \[f[x][i + j] = \sum_{t = 0}^k\binom{k}{t}g[x][t]*g[y][k-t]\]
我们发现实质上$f$的转移只与$g$有关，所以我们直接枚举指数$k$大小，$O(k)$转移即可.
上述讨论的是当$x,y$两点不都选的时候，如果都选，转移应当如下：

\[f[x][i + j + 1] = \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * (i + j + 1) ^ k \]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * (i + j + 1) ^ k \]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * \sum_{t = 0}^k(i+j)^t*1^{k-t}*\binom{k}{t}\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1}\sum_{t = 0}^k f[x][i] * f[y][j] * (i+j)^t*\binom{k}{t}\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * (i+j)^t\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * \sum_{p = 0}^ti^p*j^{t-p}*\binom{t}{p}\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} \sum_{p = 0}^t \binom{t}{p}f[x][i] * f[y][j] * i^p*j^{t-p}\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{p = 0}^t \binom{t}{p}\sum_{i = 0}^{size_x - 1}\sum_{j=0}^{size_y-1} f[x][i] * f[y][j] * i^p*j^{t-p}\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{p = 0}^t \binom{t}{p}\sum_{i = 0}^{size_x - 1} (f[x][i] * i^p) \sum_{j=0}^{size_y-1} (f[y][j] *j^{t-p})\]
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Downarrow$
\[f[x][i + j + 1] = \sum_{t = 0}^k \binom{k}{t} \sum_{p = 0}^t \binom{t}{p}g[x][p]*g[y][t-p]\]

可以发现，最后的转移，依然是只与$g$有关.
转移一个点是$O(k^2)$的，$n$个点，故时间复杂度为$O(n * k^3/6)$，实际上可以优化到$O(n*k^2)$
注意，我们如果有$a_1<a_2<\cdots a_n 且 (1\le\ a_i \le m)$，时间复杂度是$O(\frac{n^m}{n!})$

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>

#define ll long long
#define I register int
#define L register ll
#define F(i, a, b) for (L i = a; i <= b; i ++)
#define mec(a, b) memcpy(a, b, sizeof a)
#define mem(a, b) memset(a, b, sizeof a)
#define add(a, b) ((a) = (a + b) % mo)
#define N 100100
#define M 2 * N
#define Get getchar()
#define mo 998244353

using namespace std;

ll n, m, K, u, v, ans, sum, h, x, k;
ll F[N][11][2], G[N][11][2], jc[N], ny[N], d[N], bz[N];
ll nex[M], tov[M], las[N], last[N], tot;

void R(L &x) {
    char c = Get; x = 0; L t = 1;
    for (; !isdigit(c); c = Get) t = (c == '-' ? -1 : t);
    for (; isdigit(c); x = (x << 3) + (x << 1) + c - '0', c = Get); x = x * t;
}

void W(L x) {
    if (x < 0) { putchar('-'); W(-x); return; }
    if (x > 9) W(x / 10); putchar(x % 10 + '0');
}

void ins(L x, L y) { tov[++ tot] = y, nex[tot] = las[x], las[x] = tot; }

ll ksm(L x, L y) {
    L ans = 1;
    while (y) {
        if (y & 1) ans = (ans * x) % mo;
        x = (x * x) % mo, y >>= 1;
    }
    return ans;
}

ll C(L x, L y) { return jc[x] * ny[y] % mo * ny[x - y] % mo; }

void Dg_dp() {
    bz[1] = 1, d[h = 1] = 1;
    while (h) { x = d[h], k = las[x];
        if (k) {
            if (!bz[tov[k]]) bz[tov[k]] = 1, d[++ h] = tov[k];
            las[x] = nex[k];
        }
        if (!k) {
            G[x][0][0] = G[x][0][1] = 1;
            for (L k = last[x], y, s; k; k = nex[k])    
                if ((y = tov[k]) && (!bz[y])) {
                    mem(F[x], 0);
                    F(j, 0, K)
                        F(k, 0, j) {
                            add(F[x][j][0], G[x][k][0] * (G[y][j - k][0] + G[y][j - k][1]) % mo * C(j, k));
                            add(F[x][j][1], G[x][k][1] * (G[y][j - k][0]) % mo * C(j, k)); s = 0;
                            F(p, 0, k) add(s, G[x][p][1] * G[y][k - p][1] % mo * C(k, p));
                            add(F[x][j][1], C(j, k) * s);
                        }
                F(j, 0, K) G[x][j][0] = F[x][j][0], G[x][j][1] = F[x][j][1];
            }
            bz[d[h --]] = 0;
        }
            
    }
}

int main() {
    freopen("subgraph.in", "r", stdin);
    freopen("subgraph.out", "w", stdout);
    
    R(n), R(m), R(K), jc[0] = ny[0] = 1;
    F(i, 1, m) R(u), R(v), ins(u, v), ins(v, u);
    F(i, 1, K) jc[i] = (jc[i - 1] * i) % mo, ny[i] = ksm(jc[i], mo - 2);
    if (K == 0) { printf("%d", ksm(2, n)); return 0;}
    mec(last, las), Dg_dp(), W((G[1][K][0] + G[1][K][1]) % mo);
}

$T_2$

题目大意 [Ctsc2001]聪明的学生

有$3$个学生$A,B,C$，每个学生头上都贴了一个正整数，刚开始询问$A$是否猜出自己头上的正整数，如果没猜出，询问$B$，如果没猜出，询问$C$，如果没猜出，继续询问$A$……
$n$次之后一个学生猜出了自己的正整数为$m$，求所有可能的组合.
注意：稍加推理，发现每次都是头上数最大的那个人先猜出来.

数据范围

$0\lt n\lt 500, 0\lt m\lt 30000$

解题思路

先让我们看一组数据，$A,B,C=\{2,8,6\}$，$N=5,M=8$，我们来看一下为什么$B$在第五次能猜出自己头上的数是$8$.
$B$是这么想的，首先，我看到其余两个人的头上是$2,6$，那么我只有可能是$4$或$8$，假设我是$4$，如果这样的话，那么$C$第三次就可以猜出来了.
这是因为，如果我是$4$，那么$C$知道自己只有可能是$2$或者$6$，而$C$知道自己不可能是$2$，因为如果自己是$2$，$A$也是$2$，$B$直接猜出来了，所以$C$肯定了自己是$6$，但此时，聪明的$B$知道$C$并没有猜出来，这便证明了自己一定是$8$.
$ $
$ $
由上面的推导，我们不难发现，这老师不停的提问人，每一个人说能或不能，都是有价值的，但我们现在应该有疑问，在询问完一轮以后，每个人说的能或不能是否是否依然有价值.
也就是对于此题而言，$n$的用处到底是什么？
$ $
$ $
让我们再来看一组数据，$A,B,C=\{3,7,10\}$，$M=10$，假设$N=6$，我们尝试着推导一下$C$是否可以在第六次被提问时知道自己头上的数.
$C$是这么想的：
首先，$C$假设自己头上的数是$4$，那么此时$B$能否推断出自己头上的数呢？
然后，$C$觉得$B$又是这么想的：$B$可以先假设自己头上的数是$1$
那么此时很不科学，假设不是绝顶聪明的$B$觉得$A$在第四次就应该可以猜出来，为什么？
$B$想，如果我头上是$1$，那么$C$只有可能是$4$或$2$，而如果$C$是$2$，$C$第三次没猜出来，则$A$可以推断自己头上的数是$3$而非$1$，但现在关键是$B$知道$A$没能推断出自己头上的数，所以$C$只有可能是$4$
但是我们是绝顶聪明的，我们应该发现，并不能依此推断$C$就推断出自己头上的数，因为最关键的一点，在于，第一次提问$A$时，$A$并不知道$C$能否推断出，所以$A$不能推断出来自己头上的数，故$C$也不能在第三次提问时推断自己头上的数一定不是$2$
那什么时候$C$知道自己头上的数呢？只有当教授第二次问完$A$之后，$C$才能推断出自己头上的数是$4$
但此时，$B$首先一步，可$B$也无奈了，因为如果它是$1$，其余两个人是确实无法推断出来的，所以$B$也不能推断出来，既然假设$C$是$4$时，$B$无法推断自己头上的数，所以$C$此时也不能推断自己头上的数.
此时，当第$9$次提问来临，$C$牛皮了，因为此时他知道如果它头上的数是$4$，那么$B$一定可以推断出自己头上的数.
为什么？因为上面的分析中我们提到，$C$第六次提问时根据$A$没能推断出来，$C$是可以推断出来自己头上的数是$4$的，但此时，$B$知道第六次提问时$C$没能推断出来，故自己头上的数一定不是$1$，故$B$可以推测出自己头上的数就是$7$，故第九次提问时，$B$可以推测出自己头上的数，但由于$B$实质上没有推测出来，所以$C$就可以推知自己头上的数一定是$10$了.
当$C$是$10$的时候，也可以证明前八次是没有人能推断出自己头上的数的.
$ $
$ $
从上面的分析中我们不难想到，其实每一次的提问都是有绝对价值的，但即使我们分析了整个猜数的套路，我们还是难以从给定的$(N,M)$求出我们想要的$A,B,C$.

$T_3$

题目大意礼物

求\[C(n,m)\ \%\ p\]

数据范围

$n,m,p\le 10^9$，且若$p=\prod_{i=1}^{k}{p_i}^{c_i}$，则$\forall i\in [1..k]{p_i}^{c_i}\le 10^5.$

解题思路

注意到若\[p=\prod_{i=1}^{k}{p_i}^{c_i}，则\forall i\in [1..k]{p_i}^{c_i}\le 10^5.\]
于是有一个经典套路就是，求出$k$组$A_i=C(n,m)\% {p_i}^{c_i}$，最后用中国剩余定理求解.
注意到若中国剩余定理求出一组特解为$Ans$，则$(Ans+kp)$为其通解.
由于$p$不保证为质数，所以我们需要对$C(n,m)$拆式子，然后把含$p$的与不含$p$的质因子分开算.
于是问题转化为求$n!$，我们以$p^c$个数为一组，不难发现，把含$p$质因子的数筛出去后每一组的乘积在模$p^c$意义下是一样的.
这个证明很显然，因为每一组都可以表示为$(k*p^c+1,k*p^c+2,\cdots,(k+1)*p^c)$.
于是发现含有$p$的质因子又是一个阶乘.
所以分治处理.

#include <iostream>
#include <cstdio>
#include <cstring>

#define ll long long
#define I register int
#define L register ll
#define F(i, a, b) for (I i = a; i <= b; i ++)
#define Get getchar()
#define put(c) putchar(c)
#define Mxn 32000
#define Mxm 100

using namespace std;

ll n, m, p, w, ans, sum, cnt, z[Mxn];
struct pair { ll p, c, up; } sta[Mxn];
struct state { ll a, mo; } G[Mxm];
bool bz[Mxn];

void Re(L &x) {
    char c = Get; x = 0; I t = 1;
    for (; !isdigit(c); c = Get) t = (c == '-' ? -1 : t);
    for (; isdigit(c); x = (x << 3) + (x << 1) + c - '0', c = Get); x *= t;
}

void Init() {
    Re(p), Re(n), Re(m);
    F(i, 2, Mxn - 1) {
        if (!bz[i]) z[++ z[0]] = i;
        F(j, 1, z[0]) {
            if (z[j] * i >= Mxn) break;
            bz[z[j] * i] = 1;
            if (i % z[j] == 0) break;
        }
    }
    I now = p;
    F(i, 1, z[0])
        if (now % z[i] == 0) for (sta[++ cnt] = {z[i], 0, 1}; now && now % z[i] == 0; now /= z[i], sta[cnt].c ++, sta[cnt].up = sta[cnt].up * z[i]);
    if (now > 1) sta[++ cnt] = {now, 1, now};
}

ll ksm(L x, L y, L mo) {
    L s = 1;
    while (y) {
        if (y & 1) s = (s * x) % mo;
        x = (x * x) % mo, y >>= 1;
    }
    return s;
}

ll Exgcd(L a, L b, L &x, L &y) {
    if (!b) { x = 1, y = 0; return a; }
    L d = Exgcd(b, a % b, x, y), z = x;
    x = y, y = z - y * (a / b); return d;
} //拓欧

ll CALC(L st, L en, L k) { L s = 1;
    F(i, st, en) if (i % sta[k].p) s = (s * i) % sta[k].up;
    return s;
}

ll calc(L n, L k) {
    if (n <= sta[k].p) return CALC(1, n, k);
    L k1 = calc(n / sta[k].p, k); //分治求解
    L k2 = CALC(1, min(sta[k].up - 1, n), k); //每sta[k].up个分一组，这是一个循环节
    if (n > sta[k].up) {
        L k3 = CALC((n / sta[k].up) * sta[k].up + 1, n, k); //计算循环节余剩的
        return (k1 * ksm(k2, n / sta[k].up, sta[k].up) * k3) % sta[k].up;
    }
    else return (k1 * k2) % sta[k].up;
}

ll count(L n, L p) { return n < p ? 0 : n / p + count(n / p, p); } //分治计算含p质因子个数

ll Inv(L t, L p) {
    L d, x, y; d = Exgcd(t, p, x, y); //求逆元
    return (x % p + p) % p;
}

ll C(L x, L y) {
    L ss = 0;
    F(i, 1, cnt) {
        L s1 = calc(x, i), s2 = (calc(y, i) * calc(x - y, i)) % sta[i].up, tot; //计算x!/y!(x-y)!
        s1 = s1 * Inv(s2, sta[i].up) % sta[i].up; //与sta[i].up互质，所以用拓欧求逆元.
        tot = count(x, sta[i].p) - count(y, sta[i].p) - count(x - y, sta[i].p); //计算含p质因子个数
        s1 = s1 * ksm(sta[i].p, tot, sta[i].up) % sta[i].up; //快速幂一下
        G[i] = {s1, sta[i].up}; //一组方程
    }
    F(i, 1, cnt) {
        L Mi = p / sta[i].up;
        ss = (ss + ((G[i].a * Mi % p) * Inv(Mi, G[i].mo))) % p; //构造一组特解
    }
    return ss == 0 ? p : (ss % p + p) % p; //通解
}

void Doit() {
    ans = 1;
    F(i, 1, m) Re(w), ans = (ans * C(n - sum, w)) % p, sum += w; //根据题意
    printf("%lld\n", ans);
}

int main() {
    Init();
    Doit();
}

\(T_1\)

题目大意【gdoi2018 day2】第二题滑稽子图（subgraph）

数据范围

解题方案

\(Part_1\) 5%

\(Part_2\) 30%

\(Part_3\) 100% DP

\(T_2\)

题目大意 [Ctsc2001]聪明的学生

数据范围

解题思路

\(T_3\)

题目大意礼物

数据范围

解题思路

猜你喜欢

好题杂题

\(T_1\)

题目大意 【gdoi2018 day2】第二题 滑稽子图（subgraph）

数据范围

解题方案

\(Part_1\) 5%

\(Part_2\) 30%

\(Part_3\) 100% DP

\(T_2\)

题目大意 [Ctsc2001]聪明的学生

数据范围

解题思路

\(T_3\)

题目大意 礼物

数据范围

解题思路

猜你喜欢

题目大意【gdoi2018 day2】第二题滑稽子图（subgraph）

题目大意礼物