圆周率 π 是否隐藏了本个宇宙的设计者留给这个宇宙的智慧文明的某种信息？

$\pi$ 还是太naive了。我要是宇宙设计者，我就把信息藏在蔡廷常数里，这才是对人类最大的嘲讽。

蔡廷常数，其含义是找随机生成一段程序，这段程序不会陷入死循环的概率。可以证明这是一个确定存在的无理数，但是同样可以证明它是不可以被计算出来的。

实际上，能被计算出来的实数的集合是可数无穷的，所以说不能被计算出来的实数是可以计算出来的实数的无穷多倍。像 $\pi$ 这种能计算出其中任意一位的实数是少之又少的。

而蔡廷常数属于不可被计算的实数中特殊的一类数，它不仅不能计算，而且除了知道它小于1大于0以外，就连它在小数点后任意一位，包括第一位，都是可以从理论上证明是无法计算出来的【注：此处不严谨，文末有说明】。

但是呢，这个数又被证明是确实存在的一个常数。所以，我，造物主，把宇宙的秘密藏在这个数里面，我明确的告诉你们人类这一点，而你们却无可奈何。

当然，碰巧我现在心情很好，所以我大发慈悲的告诉你们，我写在蔡廷常数里面的那句话就是：你们都是虫子

————————————————————————————————————————

ps： $\pi$ 是否是正规数，和它是否被编码了没有关系啊

$\pi$ 的特殊性：

$\pi$ 是个特殊的数，不仅在于其是周长与直径之比，如果这么定义的话，在一些非欧几何中， $\pi$ 都不是常量，现在数学中使用的 $\pi$ 的定义也已经脱离了其几何含义，而将其视为微分方程中的一个常量（回想下欧拉的那个上帝公式）

$\pi$ 编码的可能性：

$\pi$ 是不是高票答案提到的正规数，和 $\pi$ 是否被特殊编码了没有关系，即使知道它是正规数，但是小说中提到的小数点后10^60 位突然出现大段的规律性编码（假设有的话），绝对是异常中的异常，因为一段长度为1000的异常编码，其期望出现的位置也应该在10^1000位之后，是穷尽整个宇宙的能量都算不出来的。

（但是！但是！因为 $\pi$ 是一个纯粹数学推理出来的产物，要能对 $\pi$ 编码，说明造物主能够任意控制这个世界的逻辑本身！这是多么难以想象的存在！）

—————————————————————————————————————

更新3：

这是第三次更新，因为看到评论区的留言，发现大家对蔡廷常数比较感兴趣，因此趁着端午佳节，来介绍一下为什么会存在不可计算的实数、蔡廷常数的历史渊源以及其重要意义。当然，这个内容就是纯粹的偏题了，若是你恰好有活动一下脑细胞的闲情雅致，则不妨慢慢看下去：

在ZFC公理体系下，实数可以分为以下几类：

存在但是不能被准确描述和定义的
能被准确的描述和定义，但是不能被计算出来的
能被计算出来的

其中第1类的数量是后两类的无穷多倍。蔡廷常数属于第2类。 $\pi$ 属于第3类。

希尔伯特在听说上面这个结论的时候，一定会回想起他在1900年向世界所有数学家提出直击数学家灵魂的希尔伯特23问的那个遥远的下午。

在工业革命之后，自然科学飞速发展，当物理学家高兴的宣布物理大厦已经建成，除了两朵乌云外晴空万里之时，数学家的世界则愁云惨淡：那些令人束手无策的难题不仅没变少，反而越来越多。当此之时，希尔伯特向全世界数学家提出了当时尚未解决但是他认为非常重要的23个问题：

其中第二个问题就是：证明算术公理的自洽性（consistency）。所谓自洽性，即一个公理体系内不应该存在矛盾，即不能存在一个命题，既能被证明又能被证伪。

第十个问题是：找到一个通用的算法，能解决所有的丢番图问题。

可以看出，虽然面临许多难题，当时的数学家还是天真的相信，一切的问题都是可以解决的，只是我们目前太弱而已。只要我们足够努力，在严格的定义和推导之下（公理化体系的建立，）我们终将可以提出一个完美的公理体系。而更乐观的数学家则相信，可以找到一个通用的算法，所有的命题都可以用这个算法来一步步的证明和证伪。

可惜这个美好愿景只是海市蜃楼，30年后，哥德尔提出了其不完备性理论打碎了数学家们的美梦：

任何一个复杂到包含了算数公理（即自然数）的公理体系，如果它是自洽的，则必然不是完备的，即必然存在一些命题，在此公理体系内部既不能被证明，又不能被证伪。
任何一个复杂到包含了算数公理（即自然数）的公理体系，其自洽性不能在该公理体系内部证明

同时图灵也提出了通用的计算模型——现代计算机的理论基础——图灵机。图灵机上有一个很重要的问题是停机问题，因为很多数学定理的证明可以归约为停机问题。

那什么是停机问题呢？停机问题是说，是否存在一个算法，对于任意一个给定的程序和输入，该算法可以判断这个程序对于这个输入的运行是否会在有限时间内终止。通俗的说就是，你在电脑上运行一个程序，然后去判断这个程序会不会陷入死循环永远停不下来。

假如我们找到了解决停机问题的方法，那么几乎所有的数学问题都可以用这个方法求解了。也就是说，这些数学问题都可以归约到停机问题上。举个例子，著名的哥德巴赫猜想：任一大于2的偶数都可写成两个质数之和。我们可以构造一个程序，这个程序会从小到大的依次对每个偶数去计算它是否可以写成两个质数的和，如果不可以，则程序退出，如果可以，则继续去枚举下一个偶数。显然，哥德巴赫猜想成立当且仅当这个程序永远不会停止。

很可惜的是，图灵证明了，停机问题是不可计算的。停机问题的不可计算性存在一个很容易看懂的不很严谨的版本，在此简要证明如下（当然你也可以先跳过这个部分，因为虽然简单，不需要任何专业知识也能看懂，但是运气不好的话在这里卡上一个小时也是不出人意料的）：

用矛盾法证明：

假设存在一个程序 $H(f)$ 可以对于任何一个程序 $f$ 判断其能否停机。那么我可以构造一个 $f$ ，将程序 $H$ 作为程序 $f$ 的子程序调用：

如果H(f)返回的结果是停机：
    进入死循环，永远不停机
否则：
    停机

可以看到，此时无论程序 $H(f)$ 的返回结果是停机还是不停机，都会导致矛盾。所以不存在能解决停机问题的通用程序。

证毕

如果你跳过了上述证明，你可以从这里开始看起：

实际上，可以进一步证明，不可计算的问题是可计算问题的无穷多倍。

不过需要特别说明的是，这里说的不可计算和我们通常理解的不可计算不是一个概念，可以说，这里讨论的不可计算比我们理解的不可计算“更加”不可计算。举个例子：

我们定义一个自然数X等于哥德巴赫猜想的真值，也就是说，如果哥德巴赫猜想为真，则X等于1，如果为假则X等于0。你可能会认为，如果能证明哥德巴赫猜想属于上面提到的既不能被证明也不能被证伪的命题，那么X就是不能被计算的了。这个想法是不对的。这里讨论的可计算性是，存在一个图灵机（或者说存在一个算法），能输出X的值，那么X就是可以计算的。显然，存在一个可以输出0的图灵机，同时存在一个可以输出1的图灵机，所以X必定可以被其中1个图灵机计算，只是我们不知道具体是哪个图灵机而已。

而我们所要讨论的不可计算的实数，则是说，不存在任何一个已知或未知的图灵机（或者说算法），能输出它的值。

ok，如果你一路辛勤的阅读至此，那么恭喜你，你已经完成了理解蔡廷的常数所需要的铺垫了，在此基础上，我们来看一个蔡廷常数的简单版例子：

首先，我们来把所有程序依次编号为1,2,3,4...，然后我们来定义一个实数X如下：X是一个大于0小于1的实数，用二进制表示，其小数点第i位等于1仅当第i个程序能在有限步内停机，否则等于0。

这也就是说，X的小数点后第i位的数字，对应了第i个停机问题的答案。用柯西序列可以证明这个实数是良定义的。如果我们能计算出X的值，那么数学的天空就会一片晴朗，因为非常多的数学问题都可以像上述的哥德巴赫猜想问题一样归约为某一个停机问题，面临这样的问题时，我们只需要查一下X的值就可以找到答案。X这个数字是如此神奇，以至于我怀疑当年Borel提出这个数字时他自己也在怀疑其可计算性吧。当然后来的事情我们都知道了，图灵证明了不存在一个算法能解决所有停机问题，而能计算出这个数字就等于能解决了所有停机问题，所以可以反证出不存在一个算法能计算出这个数字。

在计算理论里面，有一个衡量一个数字的信息量的指标叫做Kolmogorove Complexity，其含义是算出这个数字所需要的最短的程序（或者说算法）的长度。很显然，所有的有理数的信息量都是有限的，所有的代数无理数的信息量也是有限的，而对于超越数来说，存在像 $\pi$ 这样的数字，其信息量也是很少的，因为可以用一个很短的程序就可以做到输出 $\pi$ 的任意一位。但是，大多数超越数的信息量是无穷，例如上面提到的X。这意味着不存在任何一个有限长的算法可以计算出它的值。

看到这里，较真的读者可能会表示怀疑，这个X真的存在吗？上面的定义真的能准确无误的定义出一个实数吗？这个疑问是合理的，比如我用 $y^2=-1$ 来定义的y就不是实数而是复数，或者是，如果我定义y为第一个大于2且不能被写作两个质数的和的正整数，这个正整数存在的前提是哥德巴赫猜想为假，如果哥德巴赫猜想为真或不能证明其真假，则这个数字不是良定义的。因此，下面简要说明一下为什么上文提到的X是良定义的实数：

首先读者要有心理准备，无理数之所以是无理数，是因为它看起来的确不讲道理，让人难以理解，因此对此不感兴趣的读者可以直接跳过这一节。ok，废话不多说，正式开始介绍：

在我们讨论实数时，需要对什么是实数达成共识。实数的定义有很多种，每种都不是那么直观，在此我准备用柯西序列（学过高数的人肯定有印象）来构造实数。柯西序列是指这样一个无穷长的数列，它的元素随着序数的增加而愈发靠近。更确切地说，在去掉有限个元素后，可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正数。例如下图就是一个例子：

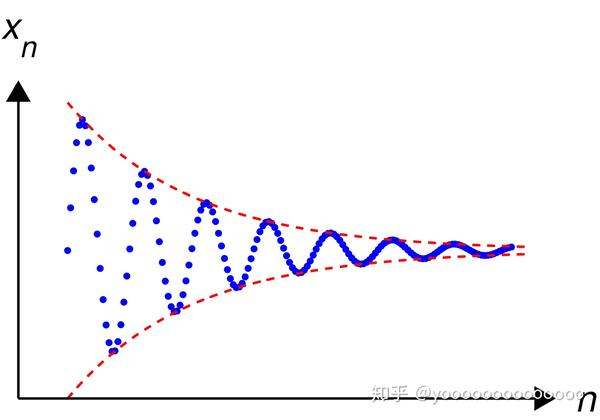
通过上图可以直观的看到，柯西序列最后会慢慢慢慢的越来越接近一个数字，无穷的接近一个数字，这时我们说，柯西序列收敛到了一个特定的数字。

对于柯西序列正式的定义是，对于有理数序列 $x_1, x_2, x_3........$ ，对于任意一个确定的 $\epsilon$ ，总是存在一个正整数 $N$ ，使得对于任意的正整数 $n,m$ ，如果 $n和m$ 均大于 $N$ ，则必有 $|x_n-x_m|<\epsilon$ 。

用有理数构造实数的方法，就是定义一个柯西序列，柯西序列每一个点都是有理数，但是最后却会收敛到一个实数上。

一个典型的例子是0.618....的那个黄金分割比，用柯西序列来定义就是： $x_n=\frac{F_n}{F_{n-1}}$ ，其中 $F_{n}$ 表示斐波那契数列的第n项。可以解得这个柯西序列收敛到 $\frac{1+\sqrt{5}}{2}$

（以上柯西序列的定义摘自维基百科：

https://zh.wikipedia.org/wiki/%E6%9F%AF%E8%A5%BF%E5%BA%8F%E5%88%97）

柯西序列是可以相加减的，两个柯西序列相加得到的新的柯西序列的第i个数字就等于原柯西序列的第i个数字的相加和。减法乘法同理。

用这个原理可以很容易证明1和0.99999999........这两个数字是相等的。

我们首先写出1的柯西序列：

1 1 1 1 1 1 ....

然后写出0.99999.....的柯西序列：

0.9 0.99 0.999 0.9999 .......

然后用前者减去后者可得：

0.1 0.01 0.001 0.0001 ......

可以看到新得到的柯西序列是收敛到0的，因此1和0.99999999........这两个数字是相等的。

好，了解了如何用柯西序列来定义实数，我们就可以开始证明Borel的X是实数了。

首先我们定义 $X$ 对应的数列的第 $n$ 项 $x_n$ 为一个二进制下 $n$ 位的有理数，其构造方式如下：将 $X$ 的前 $n$ 位对应的总共 $n$ 个程序都拿出来，对于每个程序，我们执行 $n$ 步，如果第 $i$ 个程序在前 $n$ 步内终止了，则令 $x_n$ 的第 $i$ 位为1，否则为0.

现在我们来证明上面的确定义了一个柯西序列：不失一般性的，令 $\epsilon=10^{-c}$ ，其中 $c$ 是正整数，则定义整数 $N$ 为前 $c$ 个程序中，最终会停机的那些程序里面，最长的到达停机状态的步数。换言之，必然存在一个正整数 $N$ ，使得对于前 $c$ 个程序中的任意一个最终会停机的程序，在执行 $N$ 步之后，都会停机。令 $X_c$ 表示取 $X$ 的前 $c$ 位得到的有理数，可以看到，对于任何的 $n>N$ ，都有 $X_c \leq x_n \leq X$ ，又由于 $|X-X_c|\leq \epsilon$ ，所以这是一个柯西序列

所以 $X$ 是一个良定义的实数，证毕

细心的读者可能会发现，用上面定义柯西序列的方法不就可以求解出 $X$ 了吗，这那为啥还说它是不可计算的？这不是矛盾了吗？

问的好。用上面的方法的确可以保证得到 $X$ 的任意多位的值，但是，如果真的用上面的流程来计算 $X$ 的话，我们永远没有办法知道什么时候自己手里的答案是正确的，而只能知道从某个时刻开始我们手里的答案就一直是正确的。

这么说可能比较抽象，举个例子就清楚了，例如我给你一个箱子，里面装了无数个球，每个球有个编号，编号是从1开始的自然数，我告诉你里面有3红球，剩下的都是白球，你每次可以从中拿出一个你指定的编号的球，请你设计算法找出3个红球。此时你的做法可以很简单：你就依次取出第1个球，第2个球，第3个球。。。直到你取出了3个红球为止。假设三个红球中编号最大的为W，你虽然不知道W是多少，但是你知道你的算法最后一定会在有限步内终止。

而假如同样的例子里，我告诉你里面最多有4个红球，但是不告诉你确切有几个，请你找出里面的全部红球。此时你就无能为力了，你可以一直找下去，直到找到4个红球，你就可以确定完成任务了，但是如果假设总共只有3个红球，那你就只能永远的找下去了，尽管你知道必定存在一个有限的时刻，在这个时刻之后你已经拿到了所有红球，但你永远也不知道你自己当前是在这个时刻之前还是之后。

向 $X$ 这样可以用有理数从数轴左侧无限逼近的数，叫做left enumerable computable real number(left c.e. real)，同理，那些可以用有理数从数轴右侧无限逼近的数，叫做right c.e. real。很显然，如果一个数既是left c.e. real也是right c.e. real，那么我们可以用上面类似的办法从数轴两边同时逼近它，从而求出它的任何一位来。但可惜的是，用上面的方法只能从左边去逼近 $X$ ，我们没法办法去逼近 $X$ 的上界。

如果你跳过了上述证明，你可以从这里开始看起：

另外一个值得注意的点是， $X$ 的取值是取决于我们对停机问题的排序的，例如我们可以把哥德巴赫猜想程序排在第2个位置，也可以排在第1000个位置。不同的排序对应了不同的 $X$ 。所以准确的说 $X$ 是一类数，只有当排序确定后， $X$ 才成为一个确定的数。而由于排序方法有无数种，所以从这里也可以看出，不可计算的数也有无穷多。

不过，虽然 $X$ 整体不可计算，但是其中的某些位还是可以确定的，例如，假设其第1位对应的问题是是否存在一个完全平方数，那么显然经过简单计算即可知道这一位的取值是1。而蔡廷常数就不一样了，存在一些蔡廷常数，不仅其整体不能被计算，其任何一位都不能确定。其原因在于， $X$ 的前n位储存了n个停机问题的解，而蔡廷常数的前n位储存了大约为 $2^n$ 个停机问题的解，其任何一位数字的确定都依赖于多个停机问题的解的共同作用，而用某些巧妙的方法，可以构造出这样的蔡廷常数（还记得之前说过 $X$ 的值依赖于对停机问题具体的排序吗），使得其每一位对应的停机问题中，至少有一个停机问题对应的问题是既无法被证明又无法被证伪的。

因此存在很多蔡廷常数，其每一位的值我们都不能确定！

关于这个巧妙构造的方法，因为过于复杂，在此不展开讨论，只是说下为什么蔡廷常数能做到前n位储存大约 $2^n$ 个停机问题的解。因为蔡廷常数本身的定义比较复杂，涉及到树的概念（数学上的树，是一个数据结构，和生活中的数不同），所以在此先不作讨论，而给出我自己定义的一个yo常数，但是道理是类似的。

我们的yo常数是基于之前讨论的 $X$ 来定义的，我们的目标是把信息量压缩到 $X$ 的 $\frac{6}{63}$ ，即用6位数字来储存63个停机问题的解。对于每63个停机问题，我们将其化为一组，前63个问题对应了yo常数的前6位，64到126个问题对应的是yo常数的第7到12位，以此类推。

对于每组数字的值我们这么定义：其对应的63个停机问题中，假设有x个问题是可以停机的，则该组数字对应的值等于x。显然 $0 \leq x \leq 63$ 。而0到63 在二进制下是可以用6位数字来编码的。所以x最大等于二进制下的111111

显然，可以用同 $X$ 类似的方法证明yo常数也是一个良定义的实数。下面要说明的是为什么yo常数是不可计算的。我们通过证明yo常数可以解决所有停机问题来反证：

假设我们知道yo常数的值，那么对于任意一个停机问题，我们首先找到它对应的那一组数的位置，假设该数为 $x$ ，则表示其对应的63个停机问题中有 $x$ 个是可以停机。于是我们同时运行这64个程序，直到出现 $x$ 个停机的程序，此时我们看我们要求的停机问题在不在这 $x$ 个程序里面即可。

证毕。

当然，蔡廷常数比我这个yo常数更厉害，因为它对信息的压缩率要高的多的多。讲了这么久，终于可以正式的引出我们今天的主角了。但在此之前要说明的是，其实接下来的内容不用看你也已经大致了解蔡廷常数大概是什么东西了，下面的说明无非是些具体的细节问题，不是那么重要。但是，即使有了上面那么长的铺垫，这些细节依然理解起来很有难度，所以如果你没有计算机或者数学本科背景的话，恭喜你，你已经阅读完了本篇回答了（真诚脸，相信我）。

后记：

本来只是想抖个机灵，但是看到评论区对蔡廷常数很感兴趣，因此写下了这个补充说明，开始写的时候旁边的人还在看世界杯，写完发现天已经亮了。我统计了下，这个回答总共7600字，相当于一篇论文了。讲道理除了之前的一篇介绍福特定理的回答外，我在知乎上再没有这么长的文章了，但我也深知，即使写了这么多，由于蔡廷常数涉及的前置知识确实比较难，以及我自己的文笔和水平有限，因此这样的介绍对于缺少背景知识的人来说只能是走马观花，在此表示道歉。

但尽管知道如此，我依然写出来了，因为我觉得这世上应该会有不少人和当年的我一样，对人类的认知感兴趣吧。如果你认真阅读后依然有疑惑，可以在评论区提问，我会尽量解答的。

如果你对可计算理论感兴趣，想进一步了解，但是又不是专业人士，我在此推荐一本书，叫做《哥德尔、艾舍尔、巴赫——集异璧之大成》，这本书是从科普、艺术和哲学的角度来深入浅出的讲可计算理论的，里面会从芝诺悖论开始，一步一步的带领读者走向“无穷”这个普通人最难理解的概念。但由于是科普书，我看了头几章觉得太过于科普所以没看下去，但是我的印象是，作者要实现的目标是，对于一般人来说，里面所有的内容都是虽然很烧脑但是几乎没有前置知识只要用力就肯定可以看下去的。

后记完

。

蔡廷常数

首先根据蔡廷常数的定义可知，其数值是和语言相关的。例如c语言对应了一个蔡廷常数，java又对应了一个蔡廷常数。严格来说，蔡廷常数定义在一个图灵完备的语言上，且要求该语言不存在一个语句是另一个语句的前缀。设该语言的集合为 $P_{F}$ ，则蔡廷常数的定义如下：

其中 $|P|$ 表示语句P的长度。可以证明该求和收敛，且大于0小于1.

由上述定义可知，蔡廷常数的前几位并不比后几位更加重要，所以说，只知道小数点后1到10位的值，和只知道小数点后第1000到1010位的值，没有什么差别。所以对于蔡廷常数来说，讨论近似值是没有意义的

蔡廷常数精确定义了一个实数这一点的证明方法和上文相同，在此不赘述。只特别说明一点，虽然乍一看这个求和得到的值可能大于1，但是要注意到定义里有一个前提条件，即不存在一个语句是另一个语句的前缀，根据Kraft-McMillan inequality，可证在这个前提下上述求和得到值不会超过1。

下面说明为什么蔡廷常数是不可计算的。同样此处用其可解决通用停机问题来反证，由于这个证明比较抽象，所以这里只给出简要说明：

假如我们需要求解某个程序能否停止，例如上文提到的哥德巴赫猜想程序，假设该程序长度为L。再假设我们求出了蔡廷常数为C。则我们可以用如下算法求得哥德巴赫猜想程序能否停止：

首先初始时令S等于一个空集，令实数 $C'$ 等于0。

从第1步开始，每一步执行如下操作：

对于第i步，首先我们将所有长度小于等于i的程序加入集合S。然后对于S中的每一个尚未终止的程序都运行K步（K可为任意正整数）。在这个过程中，可能会有一些之前尚未终止的程序在这一步终止，对于每一个这样的程序，假设其长度为|p|，则令 $C'=C'+2^{-|p|}$

随着上述步骤的不断执行，一定会在有限步内出现如下两种情况之一：

情况1：我们要求解的哥德巴赫猜想程序在第L步被加入了集合S，并在之后的某一步终止。由此可知，该程序会终止，哥德巴赫猜想错误

情况2：哥德巴赫猜想程序一直没有终止，但是 $C'$ 不断增大，直到在某一时刻 $C'+2^{-|L|}>C$

，由蔡廷常数的定义可知 $C'$ 是不可能大于C的，因此哥德巴赫猜想程序一定不会终止，哥德巴赫猜想由此得证

有上述算法可知，如果求出蔡廷常数，则可以求解停机问题，但停机问题又是不可解的，由此推出了矛盾。

作者：yoooooooooooooo
链接：https://www.zhihu.com/question/47610536/answer/408281314
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

圆周率 π 是否隐藏了本个宇宙的设计者留给这个宇宙的智慧文明的某种信息？

猜你喜欢