划分集合的题目----引申：数组中位数O(n)时间复杂度求法

题目

        设S是n(n为偶数)个不等的正整数的集合，要求将集合S划分为子集S1和S2，使得|S1|=|S2|=n/2，且两个子集元素之和的差达到最大。

分析

    最容易想到的做法是先进性快速排序，则前半个数组即为S1，后半个数组即为S2，然而快排的时间复杂度为O(nlgn)，而此题无需把每个元素都排好序，因此时间性能可进一步提高。此题出现在分治法的章节，因此有：利用快速排序的划分思想，设正整数集合为数组S，划分为前半个数组S1，后半个数组为S2，若第一次划分的轴值是中位数，则返回；若不是继续划分中位数所在的部分。

c++实现

/*
	程序：偶数大小的不等正整数集合划分为两个相同大小的子集，使两子集元素之和的差达到最大。
	作者：Moyu 
*/
#include<iostream>
#include<vector>
using namespace std;
/*
	函数：快速排序一次划分 
*/
int Partition(vector<int> &v, int lo, int hi)
{
	int pivot = v[lo];
	while(lo < hi)
	{
		while(lo < hi && v[hi] >= pivot)
			--hi;
		v[lo] = v[hi];
		while(lo < hi && v[lo] <= pivot)
			++lo;
		v[hi] = v[lo];
	}
	v[lo] = pivot;
	return lo;
}
/*
	函数：偶数大小数组分割，使前半部分和与后半部分和之差最大
	参数：v：偶数大小数组 lo：数组下限 hi：数组上限 
*/ 
void SetMedian(vector<int> &v, int lo, int hi)
{
	int m = Partition(v,lo,hi);
	if(m == v.size()/2 || m == v.size()/2-1)
		return;
	else{
		if(m < v.size()/2-1)
			SetMedian(v,m+1,hi);
		else
			SetMedian(v,lo,m-1);
	}
}
int main()
{
	vector<int> v{1,5,3,9,12,6,10,25,68,15};
	cout << "子集S：";
	for(auto i : v)
		cout << i << " ";
	cout << endl;
	
	SetMedian(v,0,v.size()-1);
	
	cout << "子集S1：";
	for(int i = 0; i <= v.size()/2-1; ++i)
		cout << v[i] << " ";
	cout << endl;
	cout << "子集S2：";
	for(int i = v.size()/2; i < v.size(); ++i)
		cout << v[i] << " ";
	cout << endl;
	
	return 0;
}

结果

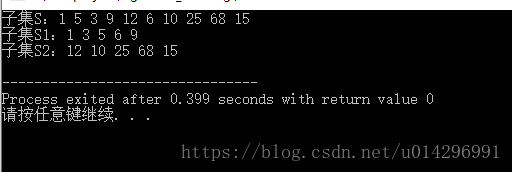
引申

    此算法时间复杂度为O(n)，利用该算法思路对程序稍加修改可以进行中位数求解，时间复杂度也为O(n)，

我称之为“中位数归位法”。对于偶数大小的数组求中位数时，可以设置两个标志，分别表示中间两元素是否都归位，当两标志为同时为true时，再返回。

箴言录：

        己欲立而立人，己欲达而达人。