原文:A Gentle Introduction to Algorithm Complexity Analysis—— By Dionyziz.
引言
如今,很多编程人员都在制作一些最酷、最实用的软件,比如我们在互联网上看到的或者每天使用的很多东西。尽管他们很多都没有计算机科学理论的背景,他们仍然是非常棒的、有创意的程序员,感谢他们所做的。
尽管如此,计算机科学理论依然有它的用途和应用,且被证明是相当实用的。在本文中,针对那些了解编程艺术但是没有任何计算机科学理论背景的程序员,我将介绍计算机科学最实用的工具之一——大写O符号和算法复杂度分析。作为在计算机科学学术界工作过,并在工业界搭建产品级软件的人,这是我在实践中发现的真正有用的工具之一,所以我希望在阅读本文后,您可以将其应用于自己的代码中,以使其更好。读完本文,您可以理解计算机科学家使用的所有常见术语,如“大写O”、“渐近行为”和“最坏情况分析”。
——略去部分——
许多行业程序员和初级学生都难以理解大写O符号和算法复杂度分析,他们为此感到恐惧并且尽量避免接触。但是,这些并不像看起来那么难以理解或理论化。算法复杂度只是一种正式测量程序或算法运行速度的方法,它确实非常实用。我们来简单介绍一下这个话题。
分析背景
我们知道,有一些称为分析器(profiler)的程序,以毫秒为单位来测量运行时间,协助我们发现运行瓶颈来优化代码。虽然这是一个有用的工具,但它与算法复杂度无关。算法复杂度是为了在理念层面上比较两种算法而设计的——忽略低级细节(如实现所用编程语言、运行算法的硬件或者给定的CPU指令集)。我们想仅依据算法本身的内容来比较算法:关于某物如何计算的理念,而统计毫秒数对此没有帮助。使用低级编程语言(如汇编)编写的差算法很可能比使用高级编程语言(如Python或Ruby)编写的好算法快得多。所以,现在是时候确定一个“更好的算法”是什么了。
算法是只执行计算的程序,而不是计算机经常执行的其它任务如网络任务或用户输入和输出。复杂度分析使得我们能够衡量程序在计算时到底有多快。纯粹计算的例子有包括数值浮点运算(如加法和乘法);在一个数据库内搜索一个给定值;确定人工智能角色在视频游戏中将要经历的路径,以便他们只需要在虚拟世界内走一小段距离(见图1);或者在字符串上运行正则表达式进行模式匹配。显然,计算在计算机程序中无处不在。

图1 视频游戏中人工智能使用算法来躲避虚拟世界的障碍
复杂度分析也是一个工具,可以让我们了解一个算法如何随着输入变大而变化。如果我们给它一个不同的输入,算法将如何表现?如果我们的算法需要1秒钟能运行1000个输入,那么如果我将输入大小加倍,它将会如何工作?它的运行速度是快一倍,还是慢四倍?在实际编程中,这非常重要,因为它使我们能够预测当输入数据变大时我们的算法将如何表现。例如,如果我们做了一个适用于1000个用户的Web应用程序,并测量其运行时间,使用算法复杂度分析,我们就可以很好地了解一旦拥有2000个用户,程序会发生什么。对于算法竞赛,复杂度分析让我们了解运行测试程序正确性的最大测试用例时,我们的代码将运行多长时间。所以如果我们测试了程序在小输入量时的行为,就可以很好地了解它是如何处理更大的输入的。我们从一个简单的例子开始:查找数组中的最大元素。
统计指令
在这篇文章中,我将使用各种编程语言来举例。如果您不知道某种特定的编程语言,请不要失望,因为既然你懂编程,即使是你不熟悉的编程语言,你也应该可以毫无问题地阅读这些例子,因为它们很简单,我不会使用任何深奥的语言特性。如果你是一个参加算法比赛的学生,你很可能使用C++,所以你应该没有问题。对于这个例子,我建议使用C++进行练习。
数组中的最大元素可以用一段简单的代码来查找,比如这段JavaScript代码。给定一个大小为n的输入数组A:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
现在,要做的第一件事是计算这段代码执行多少个基本指令,这对进一步解释我们的理论并没有太大必要,这里只做一次,所以在我分析时请多一点耐心。分析这段代码时,我们想把它分解成简单的指令,那些CPU可以直接执行或者是接近底层的东西。假设处理器可以执行下面的操作:
-
给变量赋值
-
查找数组中特定元素的值
-
比较两个值
-
值递增
-
基本的算术运算,如加法和乘法
假设分支(在if条件被判定后if...else之间的代码部分)立即发生并且不计入这些指令。在上面的代码中,第一行代码是:
var M = A[ 0 ];
这需要2条指令:一条用于读取A[0];一条用于给M赋值(假定n至少为1),无论n的值如何,这两条指令都是算法需要的。for循环初始化代码也必须始终运行,这带来了两条指令:一条赋值指令和一条比较指令:
i = 0;
i < n;
这些将在for循环第一次迭代前运行,开始循环迭代后,我们需要运行另两条指令:i自增1和一条比较指令,用于检查是否保持循环:
++i;
i < n;
所以,如果忽略循环体,这个算法需要的指令数是4 + 2n。也就是说,for循环开始处有4条指令,在n次迭代中,每次迭代结束时有2条指令。我们现在可以定义一个数学函数f(n),给定一个n时,就能知道算法需要的指令数量。对于一个空循环体,有f(n)= 4 + 2n。
最坏情况分析
现在,来看循环体:数组查找和比较必不可少:
if ( A[ i ] >= M ) { ...
这里有两条指令。但是if代码体可能运行,也可能不运行,这取决于数组的值究竟是什么。如果恰好是A [i]> = M,那么将运行这两条额外的指令——一条数组读取和一条赋值:
M = A[ i ];
但是现在要定义f(n)并不容易,因为指令数量并不仅仅依赖于n,而且还取决于我们的输入。例如,对于A = [1,2,3,4],算法将比A = [4,3,2,1]需要更多的指令。在分析算法时,我们经常考虑最坏的情况:什么是算法可能发生的最糟糕的情况?算法在什么情况下需要最多的指令来完成?在这个例子中,最坏情况就是当我们有一个按升序排列的数组时,例如A = [1,2,3,4]。在这种情况下,M需要每一次都被替换,因此产生最多的指令。
计算机科学家为此赋予一个奇特的名字,他们称之为最坏情况分析,无论如何情况都不会比这更坏的了!因此,在最坏的情况下,我们有4条指令在for循环体内运行,所以我们有f(n)= 4 + 2n + 4n = 6n + 4。函数f在给定一个问题的大小n时,能指示我们最坏情况下需要多少条指令。
渐近行为
给定f这样一个函数,使我们对算法运行有多快有了很好的概念。但是,正如我前面所说,我们不需要经历繁琐的计算指令的过程。此外,每个编程语言语句所需的实际CPU指令的数量取决于编译器和可用的CPU指令集(例如,您的PC上的处理器是AMD还是Intel Pentium,或者您的PS2上是MIPS处理器),我们希望忽略这些因素。现在通过一个“过滤器”来简化“f”函数,这将帮助我们摆脱那些计算机科学家们不愿意忽略的细节。
在函数6n + 4中,有两个因素项:6n和4。在复杂度分析中,我们只关心随着程序输入(n)的增长,指令计数函数将发生了什么。这同上面“最坏情况分析”的思想一致:我们感兴趣的是算法如何面对坏的情况,它何时会遇到具有挑战性的艰难任务。请注意,这对比较算法非常有用!如果一个算法在大量输入上击败另一个算法,那么当给定一个更简单,更小的输入时,它也很可能是更快的。从正在考虑的条件来看,我们将丢弃所有增长缓慢的因素,只保留随着n变大而快速增长的因素。显然,随着n的增大,4仍然是4,但6n越来越大,它对于更大的输入问题越来越重要。因此,我们要做的第一件事就是丢弃4,并使函数f(n)= 6n。试想,4只是一个“初始化常量”, 不同的编程语言可能需要不同的时间来设置(例如,Java需要一些时间来初始化其虚拟机),忽略这个值使得我们不用考虑编程语言的差异,这是有意义的。
我们将忽略的第二件事是n前面的常系数,如此一来函数将变成f(n)= n。正如你所看到的,这可以使事情变得非常简单。同样,如果考虑到不同语言是如何被编译的,那么放弃这个乘法常量是有意义的。“数组访问”语句会在不同的编程语言下被编译成不同的指令,例如,在C中,做A[i]不包括检查i是否符合数组大小,而在Pascal中却需要这么做。下面是Pascal代码:
M := A[ i ]
其等价于C中的
if ( i >= 0 && i < n ) {
M = A[ i ];
}
因此,我们需要考虑到对于不同的编程语言来说,在统计指令时将会有不一样的结果。 在上面的例子中,Pascal使用了一个更“笨”的编译器,它忽略了可能的优化。Pascal需要3条指令来访问每个数组元素,而C只需要一条。忽略常系数是忽略特定的编程语言和编译器之间的差异,将分析重点放在算法本身的思想上来。
如上所述的“忽略常系数”和“保留关键影响因子”的过滤器就是我们所说的渐近行为。所以f(n)= 2n + 8的渐近行为由函数f(n)= n描述。从数学上讲,渐进行为所说的是n趋于无穷大时,我们对函数f的极限感兴趣。但是如果你不明白这个词的正式含义,别担心,因为这些就是你所需要知道的(在严谨的数学问题中,我们不能将常量从极限内移除,但出于计算机科学的目的,我们需要这样做)。看几个例子来熟悉这个概念。
让我们通过忽略常系数和保留增长最快的因素项来找到以下示例函数的渐近行为。
1. f(n) = 5n + 12 得到 f(n) = n。
由于以上分析的原因。
2. f(n) = 109 得到 f(n) = 1。
忽略乘数109 * 1,但依然需要放置1在这里,以表明函数不是一个非零值。
3. f(n) = n^2 + 3n + 112 得到 f(n) = n2。
这里, n^2 比 3n 随n增长的快,因此保留它。
4. f(n) = n^3 + 1999n + 1337 得到 f(n) = n^3
虽然前面有一个很大的常系数,但我们依然可以找到一个n使得 n^3 比 1999n大。由于我们只关心n为非常大的数时候后的情况,因此只保留n^3(如图 2)。
5. f(n) = n + sqrt(n) 得到 f(n) = n。
由于n增长的比sqrt(n)快。
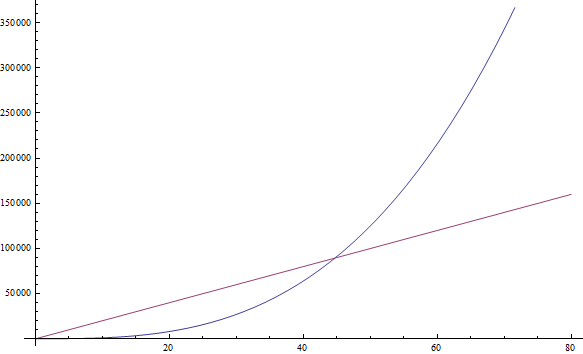
图2 蓝色绘制的n^3函数在n = 45之后比红色绘制的1999n函数大,之后一直保持
复杂度
所以这告诉我们的是,通过忽略所有这些修饰的常量,很容易就判断出程序的指令计数函数的渐近行为。实际上,没有任何循环的程序都会有f(n)= 1,因为它需要的指令数量只是一个常量(除非它使用递归;见下文)。任何具有从1到n的单循环程序都将有f(n)= n,因为它在循环之前执行恒定数量的指令,在循环之后执行恒定数量的指令,并在n次循环中每次运行恒定数量指令。
现在应该比计算独立的指令容易得多,也不那么繁琐,让我们来看几个例子来熟悉它。下面的PHP程序检查一个大小为n的数组A中是否存在一个特定的值:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
这种在数组内搜索值的方法称为线性搜索,因为这个程序的f(n)= n,所以这么说很合理(我们将在下一节中准确定义“线性”的含义)。您可能会注意到,这里有一个“break”语句,即使只迭代了一次,程序也可能会突然终止。但是请记住,我们对最坏的情况感兴趣,对于这个程序来说,最坏情况就是数组A不包含这个值。所以我们仍然有f(n)= n。
以下的C++程序检查一个大小为n的向量A是否包含相同的两个值:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
因为这里有两个嵌套的循环,我们将其渐进行为描述为为f(n)= n^2。
经验法则:简单的程序可以通过计算程序的嵌套循环来分析。n次的单层循环得到f(n)= n。双层嵌套循环得到f(n)= n^2。三层嵌套循环得到f(n)= n^3。
如果我们有一个在循环中调用函数的程序,并且知道被调用函数执行的指令的数量,则很容易确定整个程序的指令数量。我们来看看这个C例子:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
如果我们知道f(n)是一个正好执行n个指令的函数,那么我们就可以知道整个程序的指令数量是渐近n^2的,因为这个函数正好被调用n次。
经验法则:给定一系列顺序执行的for循环,其中最慢的循环决定程序的渐近行为。两个嵌套循环后跟一个单层循环,其渐进行为与仅有嵌套循环时相同,因为嵌套循环支配简单循环。
现在,让我们切换到计算机科学家使用的奇特符号。当找出了这样的渐进函数f,我们可以说程序是Θ(f(n))的,Θ(n)读作“theta of n”。有时候我们说包含常量的指令计数原始函数f(n)是Θ(某物),例如,可以说f(n)= 2n是Θ(n),也可以写成2n∈Θ(n)。这里没有什么新的东西,不要对这个表示法感到困惑,所有的意思是:如果我们已经计算出一个程序需要的指令的数量为2n,通过忽略常量,那么这个算法的渐近行为就用n来描述。 解释了这种表示法,下面是一些真正的数学表述:
n^6 + 3n ∈ Θ( n^6 )
2n + 12 ∈ Θ( 2n )
3n + 2n ∈ Θ( 3n )
n^n + n ∈ Θ( n^n )
经验法则:具有较大Θ的程序比具有较小Θ的程序运行得慢。
大O符号
特别是对于更复杂的例子,有时候我们很难正确地指出算法的行为,但是,我们可以知道算法的行为将永远不会超过一定的界限。这将使生活变得更加简单,因为不需要确切地指出算法的运行速度,我们所要做的就是找到一定的界限。这个例子很容易解释。
排序问题是计算机科学家用于算法教学的著名问题。在排序问题中,给出一个大小为n的数组A(听起来很熟悉?),要求编写程序对这个数组排序。这个问题很有趣,因为这是现实系统中的一个实际问题。例如,文件资源管理器需要按名称对其显示的文件进行排序,以便用户可以轻松地导航它们。或者另一个例子,视频游戏可能需要根据玩家眼睛在虚拟世界中的距离,来分类显示虚拟世界中的3D对象,以便确定哪些是可见的,哪些是不可见的,称为可见性问题(见图3)。最接近玩家的物体是那些可见的,而那些更远的物体可能被它们前面的物体隐藏起来。排序也很有趣,因为有很多算法可以解决这个问题,且有优劣之分,它同时也是易于定义和解释的简单问题。就让我们来编写一个排序数组的代码吧!

图3 位于黄点的玩家不会看到阴影区域。 把世界分成小片段,按距离排列,是解决可见性问题的一种方法
这是一个在Ruby中实现数组排序的低效方法(当然,Ruby支持使用你使用恰当的内置函数对数组进行排序,而这些函数肯定比我们在这里看到的要快,但这里仅仅是为了说明目的而设)。
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
这种方法被称为选择排序。它找出数组的最小值(数组表示为a,而最小值表示为m,mi是它的索引),将它放在新数组的末尾(例中的b),并将其从原始数组删除。然后接着找到原始数组剩余值之间的最小值,将其添加到新数组中,并将其从原始数组中删除,现在新数组已经有两个元素。它继续这个过程,直到所有的元素都被从原始数组中删除,并且被插入到新的数组中,这意味着数组已经被排序。
在这个例子中,我们可以看到我们有两个嵌套循环。外循环运行n次,内循环为数组a的每个元素运行一次。虽然数组a最初有n个元素,但在每次迭代中删除一个数组元素。因此,内循环在外循环的第一次迭代期间重复n次,然后是n-1次,然后是n-2次……,直到外循环的最后一次迭代为止,在该迭代期间它只运行一次。
评估这个程序的复杂度有点困难,因为必须计算1 + 2 + ... +(n-1)+ n的总和,但我们一定能确定一个“上限”。因此,我们可以改变程序(你可以用你的想法代替实际写代码来这么做),使它变得更糟,然后找到新程序的复杂度。如果能够找到构建的更糟糕的程序的复杂度,就能知道原来的程序是最坏的,或者是更好的。 如果我们发现改造的程序复杂度很好,但却比我们原来的程序更糟糕,那么可以知道原来的程序也具有相当不错的复杂度——与改造的程序一样好或是更好。
现在让我们想想编辑这个示例程序的方法,以便更容易地找出它的复杂度。但请记住,只能让它变得更糟,也即多消耗一些指令,使得估计对我们原来的计划是有意义的。显然,我们可以使程序的内部循环总是重复n次,而不是可变的次数。其中一些重复将是无用的,但它将帮助我们分析所得算法的复杂度。如果这样做,新构造的算法复杂度显然是Θ(n^2),因为有两个嵌套的循环,每个循环重复n次。像这样,我们说原来的算法复杂度是O(n^2)。O(n^2)意思是我们的程序渐近地不比n^2差,甚至可能比这更好,也可能一样好。顺便说一下,如果程序确实是Θ(n^2),我们仍然可以说它是O(n^2)。为了帮助你认识到这一点,设想改变并没有使原来程序的方式有太大变化,但是还是会使程序变得更糟,比如在程序开始的时候增加一个无意义的指令。这样做会为指令的统计结果引来一个常量,并在描述渐近行为时将它忽略。所以一个Θ(n^2)的程序也是O(n^2)的。
但是一个O(n^2)的程序可能不是Θ(n^2)。例如,除了可以为O(n)之外,任何Θ(n)的程序也是O(n^2)的。我们试想一个Θ(n)程序是一个重复n次的简单循环,我们可以通过将它装进另一个重复n次的循环中而使其变得更糟,从而产生具有f(n)=n^2的程序。概括来说,当b比a更差时,任何Θ(a)的程序都是O(b)的。请注意,我们对程序的修改并不需要具有实际上的意义或是等同于我们原来的程序。对于给定的n,它只需要比原始程序具有更多的指令,我们仅用它来影响指令的统计,而不是解决实际的问题。
所以,说程序是O(n^2)是没问题的:我们已经分析了我们的算法,发现它永远不会比n^2差,但实际上可能达到n^2,这让我们可以很好的估计程序运行速度。让我们通过几个例子来帮助你熟悉这个新的符号。
——略去练习题部分
References
1.Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
2.Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
3.Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
4.Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.
·END·
想进一步跟踪本博客动态,欢迎关注我的个人微信订阅号:信号君
信号君:寻求简单之道
技术成长 | 读书笔记 | 认知升级

扫描二维码关注信号君