动态规划最后的坑

状态压缩DP

动态规划的过程是随着“阶段”增长，在每个状态维度上不断扩展的。在任意时刻，已经求出的最优解的状态与尚未求出最优解的状态在各个维度的分界点组成了DP扩展的“轮廓”。
对于某些问题，我们需要在动态规划的“状态”记录一个集合，保存这个“轮廓”的详细信息，以便进行状态转移。若集合大小不超过N，集合中每个数都是小于K的自然数，则我们可以把集合看做一个N为K进制数，
以一个[0, K^N - 1]之间的十进制整数的形式作为DP状态的一维。
这种把集合转化为整数记录在DP状态中的一类算法，被称为状态压缩动态规划算法
在求解最短Hamilton路径时，整个状态空间可以看作n维，每维代表一个节点，只有0(尚未访问)和1(已经访问)两个值。我们可以想象DP的“轮廓”以“访问过的节点数目”为阶段，从(0,0,...,0)扩展到(1,1,...,1)。为了记录
当前状态在每个维度上的坐标是0还是1，我们使用一个N位二进制数，即[0, 2^n-1]之间的十进制整数存储节点的访问情况。另外，为了知道最后经过的节点是哪一个，我们把该节点编号作为附加信息，也保存在DP状态中。因此
该状态压缩DP的状态数组就由大小分别为2^N和N的两个维度构成。

例题1: Mondriaan's Dream(poj2411)
求把N*M(1 <= N,M <= 11)的棋盘分割成若干个1 * 2的长方形，有多少种方案。例如当N=2, M=3时，有3种方案。
输入包含多个测试用例。每个测试用例由两个整数组成：大矩形的高度H和宽度W。输入由H＝W＝0终止。否则，1＜h，w＜11。

Sample Input

Sample Output

首先假设我们要对棋盘进行切割，有横切和纵切这两种思路，按照DP的思想，为了方便，将每一行划分为阶段，由上一行对下一行进行扩展，
这样我们想对于这一行的切割，有一次切出1*2的长方形和先切出1*1两种方式
例如：

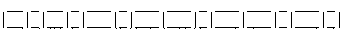
那么这样除了一些符合条件的1*2长方形，还存在一些只被切了一半的1*1的长方形，这些是不符合条件的。我们想根据题目是不能出现只有一半的长方形的
所以这些残缺体必然会在下一行被补齐，这样我们就需要知道哪些是未补齐的残缺体，我们使用一个M位的二进制数，对于这个二进制数的M位，当某一位是1时，我们设这表示有一个残缺体需要补齐，当某一位为0时，表示这是一个
横着的1*2的长方形或是已经补齐的竖着的1*2长方形，总之就是其余状态
这样我们设f[i, j]表示第i行的情况的形态为j的二进制数时，前i行切割的方案总数.(j是用十进制表示的M位二进制数)
思考转移情况
对于第i-1行转移到第i行，形态从k转移到j，当且仅当：
1.j与k按位与后全为0.
这保证了每个数字1下方必须是数字0，代表继续补齐了竖着的长方形
2.j和k按位或后的结果的二进制表示中，每一段连续的0必须是偶数个
这些0代表若干个横着的1*2长方形，奇数个0无法分割出这种形态
但是我们对于j和k的比对计算，是已经默认了j和k都已知了，一方面确实我们可以通过枚举j和k，但是不可避免的会有完全不符合题目的j和k因此我们可以在DP前先预处理出[0, 2^m-1]内所有满足“二进制表示下每一段连续的0有
偶数个”的整数，记录在集合S中。
f[i, j] = ∑f[i - 1, k](j&k==0 并且 j|k∈s)
初值:f[0, 0] = 1,其余均为0
目标:f[N, 0]
时间复杂度O(2^M2^MN) = O(4^MN)（当然不是我自己算的，我不会算=-=）

 1 #include<iostream>
 2 #include<iomanip>
 3 #include<cstdio>
 4 #include<ctime>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<cmath>
 8 #include<cstdlib>
 9 #define ll long long
10 using namespace std;
11 int n, m;
12 ll f[12][1 << 11];
13 bool vis[1 << 11]; 
14 int main() {
15     while(cin >> n >> m && n) {
16         memset(vis, 0, sizeof(vis));
17         memset(f, 0, sizeof(f));
18         for(int i = 0; i < 1 << m; ++i) {
19             bool flag1 = 0, flag2 = 0;
20             for(int j = 0; j < m; ++j) {
21                 if(i >> j & 1) flag1 |= flag2, flag2 = 0;
22                 else flag2 ^= 1;//只要0不是连续的，就激活flag1(flag1 = 1)，则此时无论后面flag2为多少，最终都不满足 
23             }
24             vis[i] = flag1 | flag2 ? 0 : 1;//flag1 | flag2 == 1,取0，否则取1 
25         }
26         f[0][0] = 1;
27         for(int i = 1; i <= n; ++i) {
28             for(int j = 0; j < 1 << m; ++j) {
29                 f[i][j] = 0;
30                 for(int k = 0; k < 1 << m; ++k) 
31                     if((j & k) == 0 && vis[j | k]) 
32                         f[i][j] += f[i - 1][k];
33             }
34         }
35         cout << f[n][0] << '\n';//最后分割完的大矩形，一定不存在空缺，其M位二进制数表示一定为0 
36     }
37     return 0;
38 }

还是很难想的啊=-=

动态规划最后的坑

状态压缩DP

猜你喜欢