splay、treap、SBT（Size Balanced Tree）那点奇诡的东东（填坑ing）

当然要在前面先哔一哔

（首先，不知道BST是什么的话……戳这里）

众所周知BST的期望复杂度为$O(log_2n)$，但数据用链卡直接就成了$O(n)$的复杂度
人类的智慧是伟大的，这时，BBT们就该出场了
BBT（平衡树），有red black tree、AVL、替罪羊、treap、splay等
BBT采取了某些和谐的思想，把原本卡成链复杂度接近$O(n)$的BST，重新变回$O(log_2n)$的复杂度

---

splay

接下来，该介绍今天的主角——splay了

---

没用的东西我们学来干嘛？

splay，中文名伸展树、分裂树，BBT的一种，实际是BST的神奇优化
（英文名叫splay或者是spaly，我不知道，所以都称作splay了）

• splay可以$O(log_2n)$时间插入、查找以及删除，速度快到飞起，用途广，代码复杂度不高

• 其实真正的情况是，所有能用线段树做的题目都能用splay切掉！

• 比起其他BBT，splay不用记录某些东东，空间比其他BBT优

• 仅是用旋转来让整课树不退化成链，这点和treap有点像

• 但时间复杂度可是相当的不稳定……这个等会再解释

那就，不管那么多了

---

脑残的旋转

What are rotates？

在放图片前说一下
splay旋转的目的是让一个节点通过旋转成为另一个节点的儿子节点，然后进行单点或区间操作
（最基础的两个旋转和treap的两个旋转是一样的，但是双旋……咳咳）

---

how to rotate？

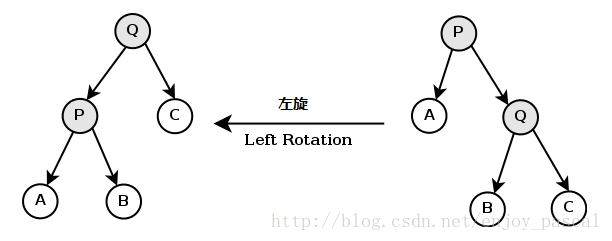
left rotate

左旋：把p的右儿子q旋转，使q成为p的父亲

左旋步骤

• 把q的父亲标记为p的父亲（即q的祖父）

• 把p的父亲标记为q

• 此时q有三个儿子节点，为了保证splay tree是二叉树，再把q的左儿子B的父亲标记为p

（不懂就画个图，清晰明了）

由右图可知：A < P < B < Q < C
从右树转到左树，虽然节点位置发生了变化，但$A < P < B < Q < C$ 仍成立
BST性质没有被破坏

---

left rotate code

void left_rotate(int x)
{
    downdata(father[x]);
    downdata(x);
    int y=father[x],z=father[y];
    father[x]=z,father[y]=x;
    if (z==0)root=x;
    else
    {
        if (tree[z][1]==y)
        {
            tree[z][1]=x;
        }
        else tree[z][2]=x;
    }

    if (tree[x][1])
    {
        father[tree[x][1]]=y;
    }
    tree[y][2]=tree[x][1];
    tree[x][1]=y;

    size[y]=size[tree[y][1]]+size[tree[y][2]]+1;
    size[x]=size[y]+size[tree[x][2]]+1;
}

---

right rotate

右旋：把q的左儿子p旋转，使p成为q的父亲

步骤、性质和左旋同理，这里不再多讲

---

right rotate code

void right_rotate(int x)
{
    downdata(father[x]);
    downdata(x);
    int y=father[x],z=father[y];
    father[x]=z,father[y]=x;

    if (z==0)root=x;
    else
    {
        if (tree[z][1]==y)
        {
            tree[z][1]=x;
        }
        else tree[z][2]=x;
    }
    if (tree[x][2])
    {
        father[tree[x][2]]=y;
    }
    tree[y][1]=tree[x][2];
    tree[x][2]=y;

    size[y]=size[tree[y][1]]+size[tree[y][2]]+1;
    size[x]=size[tree[x][1]]+size[y]+1;
}

---

单旋

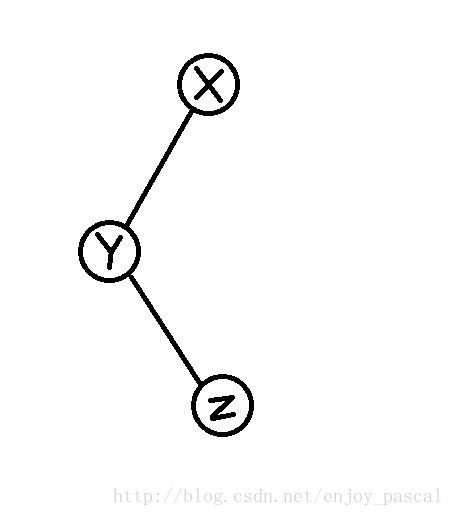
我们在这里，需要把z旋转到x的儿子节点（当x是z的祖父的时候）

直接左旋z

---

直接右旋z

单旋一共只有两种情况
（其实旋转很简单……自己心神意会一下）

---

more scientific rotates

简单不？简单，不过您以为这就完了？
OK经过一堆的单旋以后，splay树可能变成这样：

（可以自己思考思考为什么splay tree会变成这个狗(ノ=Д=)ノ┻━┻样）

THEREFORE，我们需要更加科学的方法

---

双旋

比如我们要把$α$这个节点旋转到节点$β$的儿子节点
如果现在$α$的父亲、祖父都不是$β$的话，我们就需要双旋

双旋的时间复杂度Tarjan证过均摊 $O(log_2n)$，而单旋是$O(n)$，速度差别很大

注意是均摊……均摊……均摊，不是期望！这就是splay时间复杂度不稳定的原因

双旋一共有四种情况

---

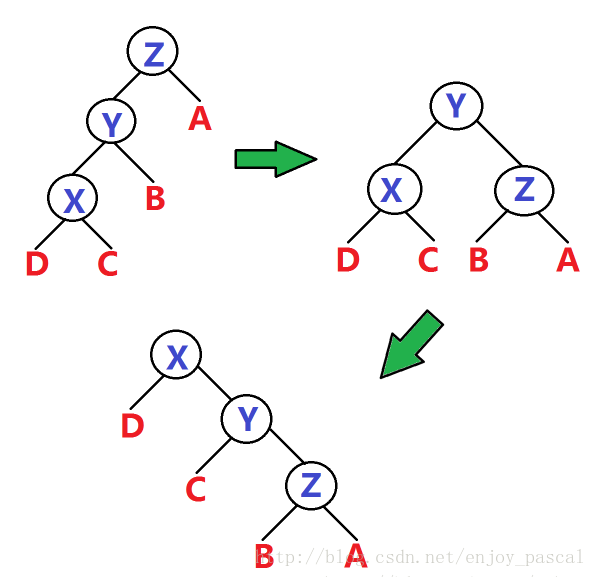
situation one

下图是把x旋到z以上的某个父亲节点

明显，先右旋y，再右旋x

---

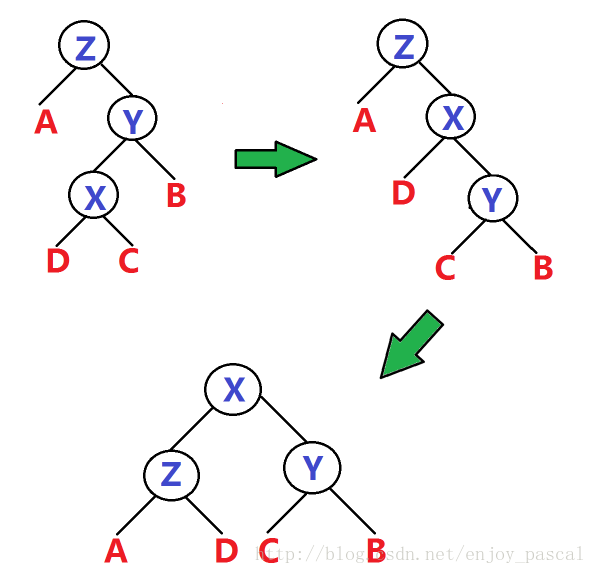
situation two

下图是把z旋到x以上的某个父亲节点

同样的，先左旋y，再左旋z

上面两个是成一条链的情况

---

situation three and four

下图是把x旋到z以上的某个父亲节点

这里很显然，先右旋x再左旋x

情况四和情况三是差不多的，即z的左儿子是y、y的右儿子是x，双旋是先左旋x再右旋x

图就不用再贴了

---

splay code

单旋叫做spaly，双旋叫做splay，额貌似是这样？
哎算了不管那么多了￣3￣

反正我很确定的一点就是双旋的过程就被称作splay！

void splay(int x,int y)
{
    if (x==y || x==0)return;
    while (father[x]!=y)
    {
        if (father[father[x]]==y)
        {
            if (tree[father[x]][1]==x)
            {
                right_rotate(x);
            }
            else left_rotate(x);
        }
        else
        {
            if (tree[father[father[x]]][1]==father[x] && tree[father[x]][1]==x)
            {
                right_rotate(father[x]);
                right_rotate(x);
            }
            else if (tree[father[father[x]]][1]==father[x] && tree[father[x]][2]==x)
            {
                left_rotate(x);
                right_rotate(x);
            }
            else if (tree[father[father[x]]][2]==father[x] && tree[father[x]][1]==x)
            {
                right_rotate(x);
                left_rotate(x);
            }
            else if (tree[father[father[x]]][2]==father[x] && tree[father[x]][2]==x)
            {
                left_rotate(father[x]);
                left_rotate(x);
            }
        }
    }
}

---

find

splay的查找（find）和普通BST的查找并没有什么卵区别
由于BST性质，比当前节点关键字小就往左边找，大就往右边找，刚刚好不就找到了嘛

---

some properties

恩设当前的节点为$now$，左儿子为$now_{left}$，右儿子为$now_{right}$
设$size[x]$表示以$x$为根的树有多少个节点，那么$now$在以now为根的树里，它的下标是第$size[now_{left}]+1$小
（这是性质不要问我为什么因为splay它就是这样）

---

one of two issues

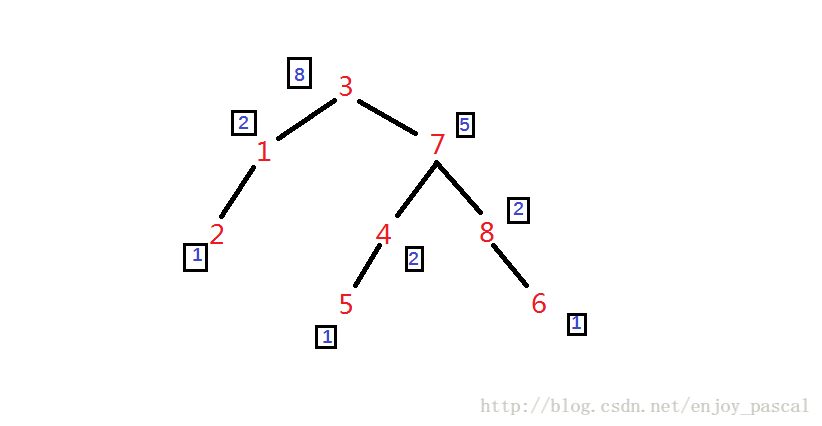
可能说的有点反人类，so我鼠绘了个东东（红色数字是维护的值，蓝色的是size）

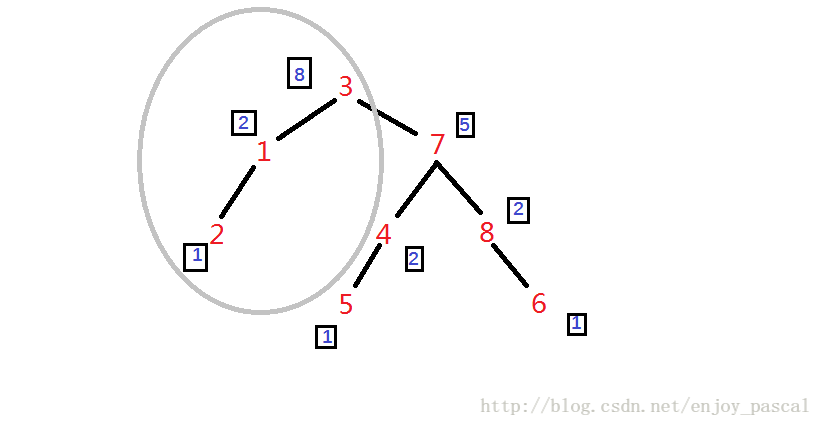
如果我们现在从根节点（维护的值为3的节点）开始，找第一小的数
由于$size[root_{left}]$是$2$，所以根节点是下标第三小的节点

根据BBT性质，第一小的数在根的左子树上
于是愉快地向根的左儿子继续寻找，接着同理，所以在整棵树里面下标最小的是维护的值为2的节点

---

the other issue

如果我们从根节点开始，找下标第四小的呢？

显然的是下标第四小的点肯定不在根的左子树上，所以我们要往根的右子树上去找
找？找什么？怎么找？

由于根和根的左子树有三个节点，所以在找全棵树的节点下标第四小的时候，要把前面三个节点减去
既然$4-3=1$，所以我们接下来应该找根的右子树中，节点下标第一小的节点

不简单吗？当然简单了……
这里不存在感性理解

---

find code

int find(int x,int y)
{
    /*
    if (tree[x][1])
    {
        downdata(tree[x][1]);
    }
    if (tree[x][2])
    {
        downdata(tree[x][2]);
    }
    */
    if (y==size[tree[x][1]]+1)return x;
    else
    {
        if (y<size[tree[x][1]]+1)return find(tree[x][1],y);
        else return find(tree[x][2],y-size[tree[x][1]]-1);
    }
}

---

例题万岁！

例题1：【线段树】最大值

problem

题目描述

在N（1<=N<=100000）个数A1…An组成的序列上进行M(1<=M<=100000)次操作，操作有两种：

(1)1 x y：表示修改A[x]为y；

(1)2 x y：询问x到y之间的最大值。

输入

第一行输入N(1<=N<=100000)，表示序列的长度，接下来N行输入原始序列；接下来一行输入M(1<=M<=100000)表示操作的次数，接下来M行，每行为1
x y或2 x y

输出

对于每个操作(2)输出对应的答案。

样例输入

5 1 2 3 4 5 3 2 1 4 1 3 5 2 2 4

样例输出

4 5

数据范围限制

提示

【限制】

保证序列中的所有的数都在longint范围内

---

analysis

线段树裸题，但我要用splay把它切了！

---

例题2：【NOIP2015模拟9.12】平方和

problem

Description

给出一个N个整数构成的序列，有M次操作，每次操作有一下三种：
①Insert Y X，在序列的第Y个数之前插入一个数X；
②Add L R X，对序列中第L个数到第R个数，每个数都加上X；
③Query L R，询问序列中第L个数到第R个数的平方和。

Input

第一行一个正整数N，表示初始序列长度。 第二行N个整数Ai，表示初始序列中的数。 第三行一个正整数M，表示操作数。
接下来M行，每行一种操作。

Output

对于每一个Query操作输出答案。由于答案可能很大，请mod 7459后输出。

Sample Input

5 1 2 3 4 5 5 Query 1 3 Insert 2 5 Query 2 4 Add 5 6 7 Query 1 6

Sample Output

14 38 304 样例解释： 第二次操作后的序列：1，5，2，3，4，5。 第四次操作后的序列：1，5，2，3，11，12。

Data Constraint

30%的数据满足N≤1,000，M≤1,000。 另外20%的数据满足N≤100,000，M≤100,000，且不存在Insert操作。
100%的数据满足N≤100,000，M≤100,000，且Add和Insert操作中|X|≤1000，|Ai|≤1000。

---

analysis

• 这题会了上面的splay操作，就很简单了

• 用splay维护两个值，和$sum[x]$与平方和$sqrsum[x]$

• 每次一个位置$x$加上$a$，$sqrsum[x]$就会加上$a^2∗size[x]+2a∗sum[x]$，$sum[x]$会加上$a∗size[x]$

• 当然这里的$a$看作$flag$标记向下传就可以了，跟线段树的标记差不多

• 通过find和splay操作进行插入节点

• 即可AC

---

code

#include<bits/stdc++.h>
#define MAXN 200001
#define mod 7459

using namespace std;

long long tree[MAXN][3],sum[MAXN],sqrsum[MAXN];
long long a[MAXN],father[MAXN],size[MAXN],flag[MAXN];
int n,m,root;
char s[11];

void downdata(int x)
{
    if (!flag[x])return;
    if (tree[x][1])
    {
        flag[tree[x][1]]+=flag[x];
    }
    if (tree[x][2])
    {
        flag[tree[x][2]]+=flag[x];
    }
    sqrsum[x]=(((sqrsum[x]+((flag[x]*flag[x])%mod)*size[x])%mod)+2*flag[x]*sum[x])%mod;
    sum[x]=sum[x]+flag[x]*size[x];
    tree[x][0]+=flag[x];
    flag[x]=0;
}

void left_rotate(int x)
{
    downdata(father[x]);
    downdata(x);
    int y=father[x],z=father[y];
    father[x]=z,father[y]=x;
    if (z==0)root=x;
    else
    {
        if (tree[z][1]==y)
        {
            tree[z][1]=x;
        }
        else tree[z][2]=x;
    }

    if (tree[x][1])
    {
        father[tree[x][1]]=y;
    }
    tree[y][2]=tree[x][1];
    tree[x][1]=y;

    size[y]=size[tree[y][1]]+size[tree[y][2]]+1;
    size[x]=size[y]+size[tree[x][2]]+1;

    sum[y]=(sum[tree[y][1]]+sum[tree[y][2]]+tree[y][0])%mod;
    sum[x]=(sum[y]+sum[tree[x][1]]+tree[x][0])%mod;

    sqrsum[y]=(sqrsum[tree[y][1]]+sqrsum[tree[y][2]]+tree[y][0]*tree[y][0])%mod;
    sqrsum[x]=(sqrsum[y]+sqrsum[tree[x][2]]+tree[x][0]*tree[x][0])%mod;
}

void right_rotate(int x)
{
    downdata(father[x]);
    downdata(x);
    int y=father[x],z=father[y];
    father[x]=z,father[y]=x;

    if (z==0)root=x;
    else
    {
        if (tree[z][1]==y)
        {
            tree[z][1]=x;
        }
        else tree[z][2]=x;
    }
    if (tree[x][2])
    {
        father[tree[x][2]]=y;
    }
    tree[y][1]=tree[x][2];
    tree[x][2]=y;

    size[y]=size[tree[y][1]]+size[tree[y][2]]+1;
    size[x]=size[tree[x][1]]+size[y]+1;

    sum[y]=(sum[tree[y][1]]+sum[tree[y][2]]+tree[y][0])%mod;
    sum[x]=(sum[tree[x][1]]+sum[y]+tree[x][0])%mod;

    sqrsum[y]=(sqrsum[tree[y][1]]+sqrsum[tree[y][2]]+tree[y][0]*tree[y][0])%mod;
    sqrsum[x]=(sqrsum[tree[x][1]]+sqrsum[y]+tree[x][0]*tree[x][0])%mod;
}

void splay(int x,int y)
{
    if (x==y || x==0)return;
    while (father[x]!=y)
    {
        if (father[father[x]]==y)
        {
            if (tree[father[x]][1]==x)
            {
                right_rotate(x);
            }
            else left_rotate(x);
        }
        else
        {
            if (tree[father[father[x]]][1]==father[x] && tree[father[x]][1]==x)
            {
                right_rotate(father[x]);
                right_rotate(x);
            }
            else if (tree[father[father[x]]][1]==father[x] && tree[father[x]][2]==x)
            {
                left_rotate(x);
                right_rotate(x);
            }
            else if (tree[father[father[x]]][2]==father[x] && tree[father[x]][1]==x)
            {
                right_rotate(x);
                left_rotate(x);
            }
            else if (tree[father[father[x]]][2]==father[x] && tree[father[x]][2]==x)
            {
                left_rotate(father[x]);
                left_rotate(x);
            }
        }
    }
}

int find(int x,int y)
{
    if (tree[x][1])
    {
        downdata(tree[x][1]);
    }
    if (tree[x][2])
    {
        downdata(tree[x][2]);
    }
    if (y==size[tree[x][1]]+1)return x;
    else
    {
        if (y<size[tree[x][1]]+1)return find(tree[x][1],y);
        else return find(tree[x][2],y-size[tree[x][1]]-1);
    }
}

int main()
{   
    //freopen("readin.txt","r",stdin);

    scanf("%d",&n); 
    root=1,tree[1][2]=2;

    for (int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i+1]);
        father[i+1]=i;
        tree[i+1][0]=a[i+1];
        tree[i+1][2]=i+2;
        size[i+1]=n+2-i;
    }
    n+=2;
    for (int i=n-1;i>=1;i--)
    {
        sum[i]=(sum[i+1]+a[i])%mod;
        sqrsum[i]=(sqrsum[i+1]+a[i]*a[i])%mod;
    }
    size[1]=n,size[n]=1;
    father[n]=n-1;
    scanf("%d",&m);
    for (int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%s%d%d",&s,&x,&y);
        if (s[0]=='Q')
        {
            int j=find(1,x),k=find(1,y+2);
            splay(j,1),splay(k,j);
            printf("%lld\n",(sqrsum[tree[k][1]]+mod)%mod);
        }
        else if (s[0]=='I')
        {
            int j=find(1,x),k=find(1,x+1);
            splay(j,1),splay(k,j);
            tree[++n][0]=y,tree[n][1]=tree[n][2]=0;
            father[n]=k;
            tree[k][1]=n;
            sum[n]=y%mod,sqrsum[n]=y*y%mod;
            size[n]=1;
            sum[j]=(sum[j]+y)%mod,sum[k]=(sum[k]+y)%mod;
            sqrsum[j]=(sqrsum[j]+y*y)%mod,sqrsum[k]=(sqrsum[k]+y*y)%mod;
            size[j]++,size[k]++; 
        }
        else
        {
            scanf("%d",&z);
            int j=find(1,x),k=find(1,y+2);
            splay(j,1),splay(k,j);
            flag[tree[k][1]]+=z;
            downdata(tree[k][1]);
        }
    }
    return 0;
}

---

treap

---

SBT（Size Balanced Tree）

---

为什么blog的末尾不哔一哔呢？