前面简单讲了机械臂的正解问题,即通过原位姿和控制各关节的角度得到终点位姿。而在实际应用的时候,我们通常都是知道起始点和末端终点的位姿,需要考虑如何达到,即运动学机械臂的运动学逆解问题。
求解操作臂运动学方程是一个非线性问题。我们需要考虑解的存在性、多重解性以及求解方法。
![]()
1.解的存在性
解是否存在的问题完全取决于操作臂的工作空间。工作空间是操作臂末端执行器所能达到的范围。如果解存在,则被指定的目标点必须在工作空间内。灵巧工作空间是指机器人的末端执行器能后从各个方向达到的空间区域,可达工作区间是机器人至少从一个方向上有一个方位可以达到的空间。灵巧工作空间是可达工作空间的子集。
 2.多重解问题
2.多重解问题
在求解过程中可能遇到另一个问题就是多重解问题。
解的选择标准。最短形成?权重?干涉?

 3.解法
3.解法

 代数解法
代数解法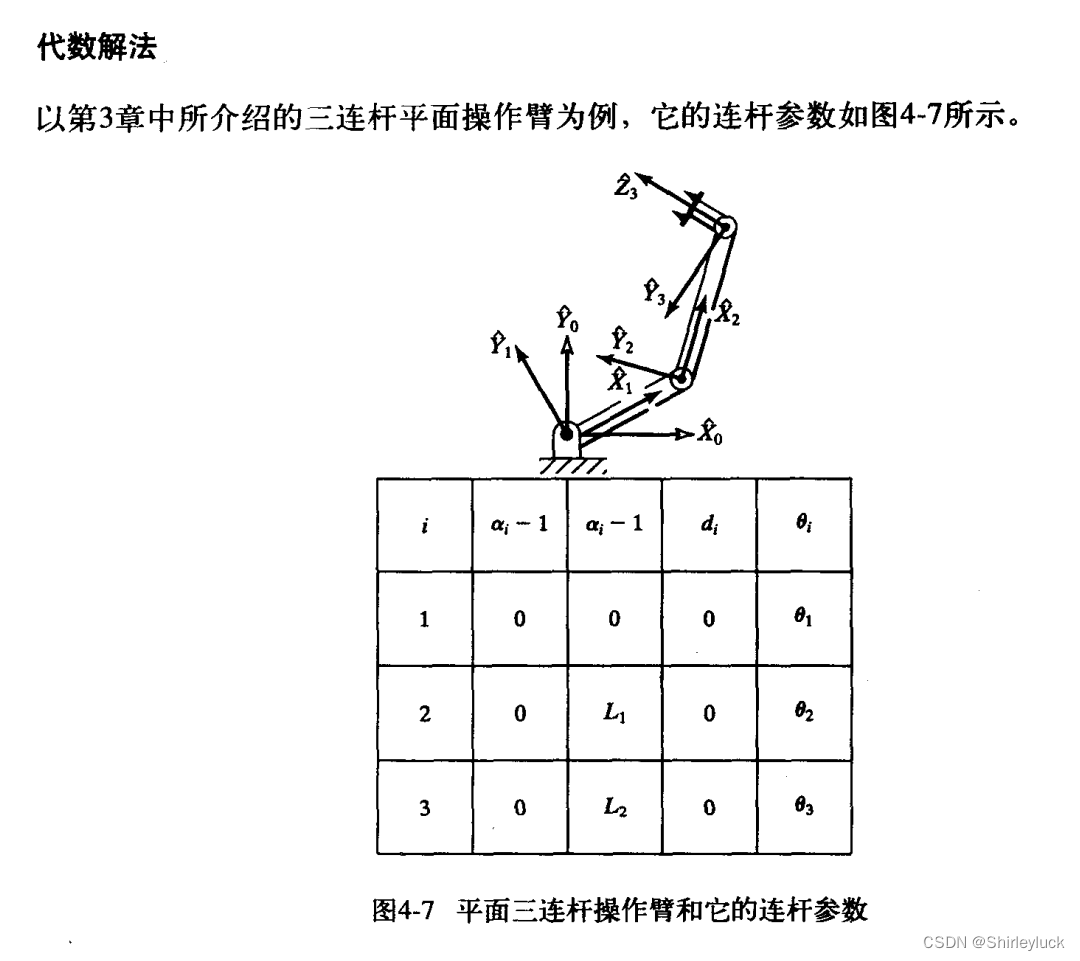

二幅角反切公式:



几何解


4.MATLAB 实操
这真的是一件难过的事情,在求逆解的时候我曲曲折折烦躁不已,还是没有很好地求出来,还是参考了其他同学的代码。本来想通过控制几何关系来求解,但是应该是一堆bug,已经无力修改了,如果有人帮忙看看问题是什么就更好了
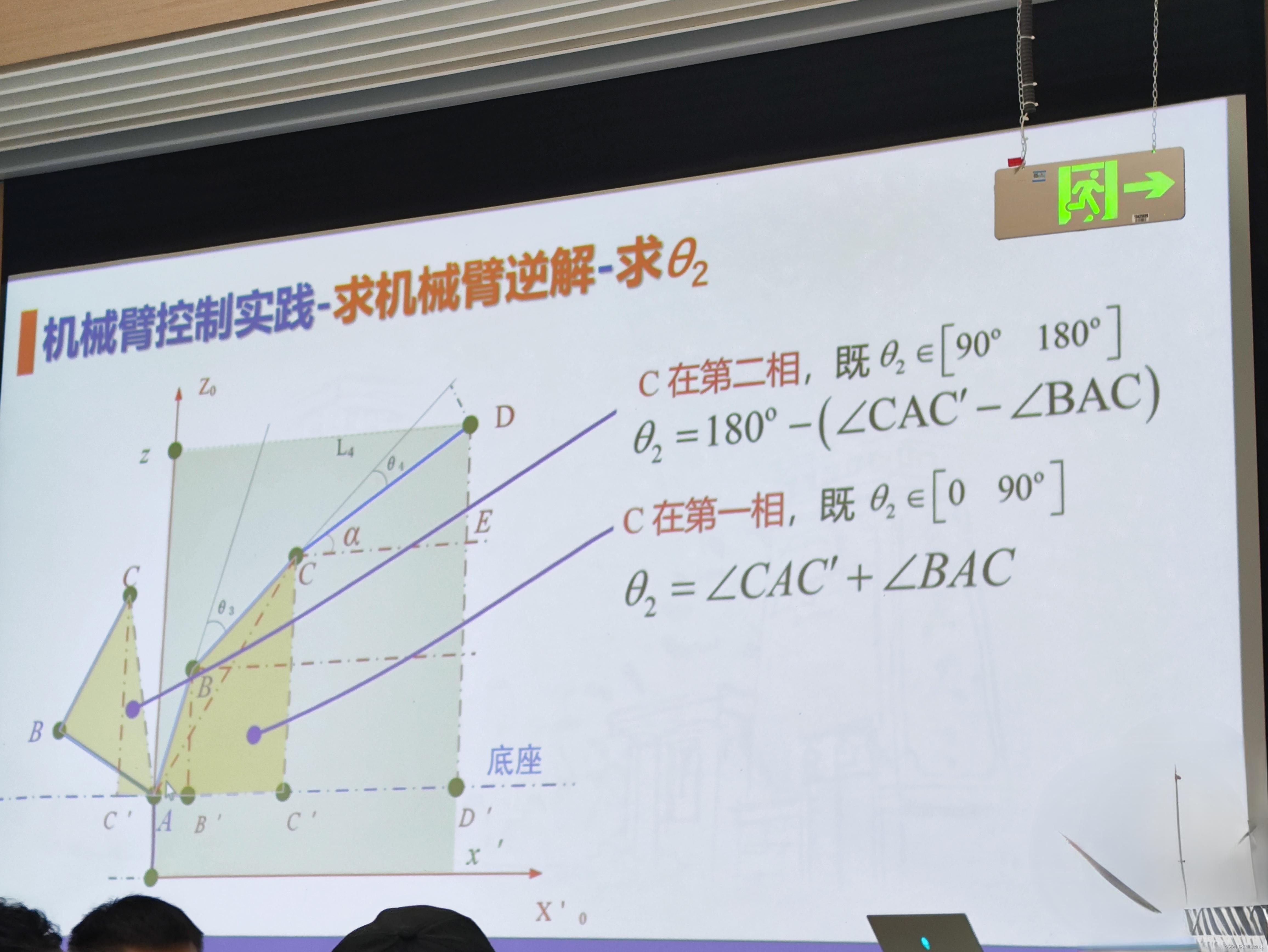
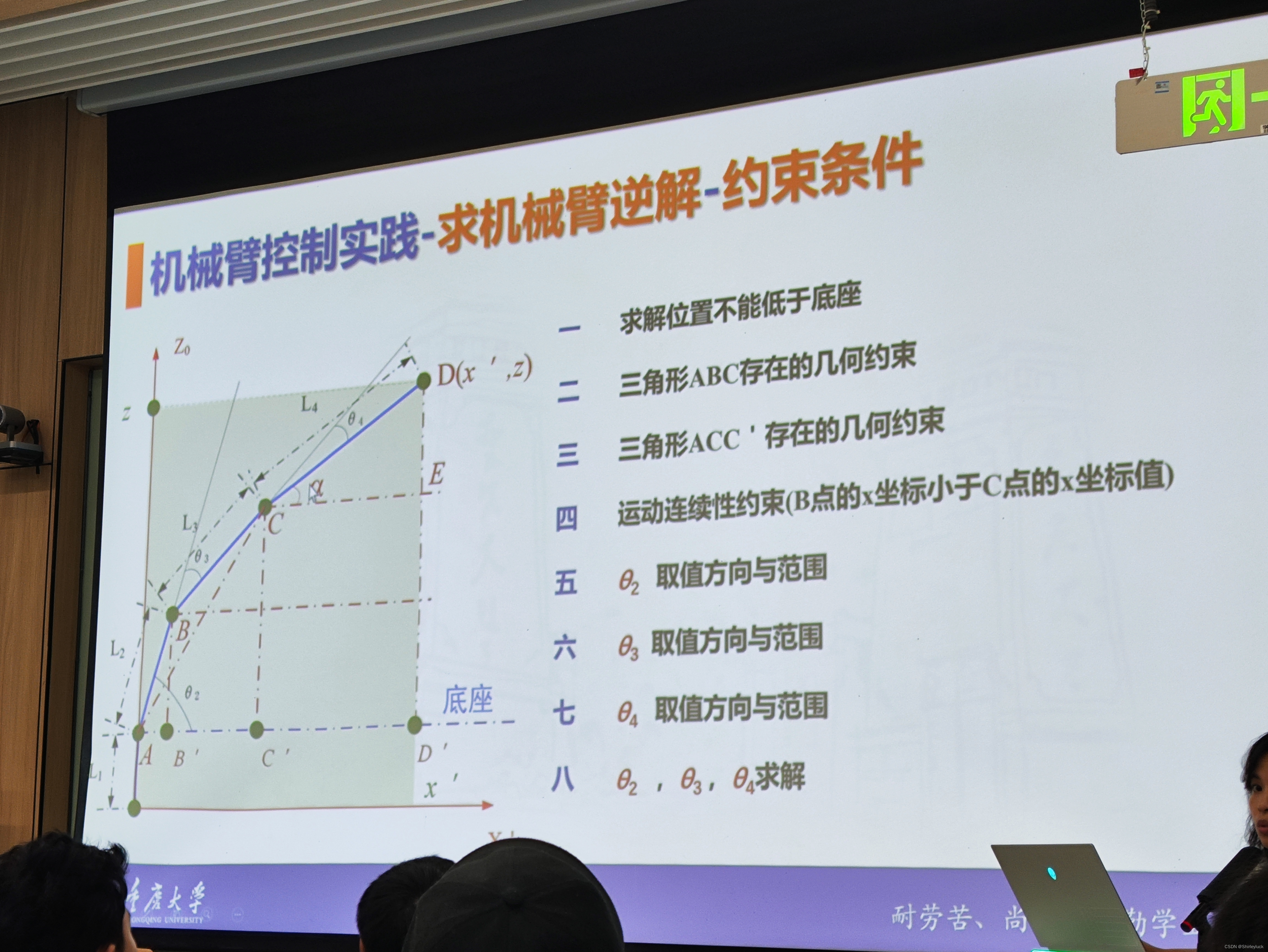

clear; clc;
%% 参数
L1 = 100;
L2 = 105;
L3 = 98;
L4 = 245;
IN_theta = [0, -45, 30,10, 0];
% DH 参数
C_a = [0, 0, L2, L3, 0, 0, 0];
C_d = [0, L1, 0, 0, 0, 0, L4];
C_alpha = [0, -90, 0, 0, -90, 0, 0];
C_theta = [0, IN_theta(1), IN_theta(2), IN_theta(3), IN_theta(4)-90, IN_theta(5), 0];
T_target = eye(4); % 初始化结果为单位矩阵
for i = 1:6
T = [cosd(C_theta(i+1)), -sind(C_theta(i+1)), 0, C_a(i);
sind(C_theta(i+1))*cosd(C_alpha(i)), cosd(C_theta(i+1))*cosd(C_alpha(i)), -sind(C_alpha(i)), -sind(C_alpha(i))*C_d(i+1);
sind(C_theta(i+1))*sind(C_alpha(i)), cosd(C_theta(i+1))*sind(C_alpha(i)), cosd(C_alpha(i)), cosd(C_alpha(i))*C_d(i+1);
0, 0, 0, 1]; % 根据给定的公式计算 T[i]
T_target = T_target * T; % 乘以每个 T[i]
end
% 提取目标位置
x_target = T_target(1, 4);
y_target = T_target(2, 4);
z_target = T_target(3, 4);
% 初始化最优解
best_theta = [];
min_error = inf;
%% 逆运动学求解
for apha1 = -90:1:90 % L4与x轴的夹角,角度步长为1度
% 方程组定义
syms theta2 theta3 theta4
% 几何约束条件
eq1 = L4 * cosd(apha1) + L3 * cosd(apha1 + theta4) + L2 * cosd(theta2) == x_target;
eq2 = L1 + L4 * sin(apha1) + L3 * sind(apha1 + theta4) + L2 * sind(theta2) == z_target;
eq3 = theta2 == apha1 + theta3 + theta4;
%eq4 = cos(2/pi + theta2 + theta4 + deg2rad(apha1)) == (L2^2 + L4^2 - (L3 * cosd(apha1 + theta4) + L2 * cosd(theta2))^2 + (L3 * sind(apha1 + theta4) + L2 * sind(theta2))^2) / (2 * L2 * L3);
% 几何约束的非负性
%condition1 = L1 + L2 * cosd(theta2) > 0;
%condition2 = L1 + L3 * cosd(apha1 + theta4) + L2 * cosd(theta2) > 0;
% 组合所有方程和约束条件
equations = [eq1, eq2, eq3];
% 求解方程组
solutions = solve(equations, [theta2, theta3, theta4], 'Real', true);
% 提取并验证解
theta2_sol = double(solutions.theta2);
theta3_sol = double(solutions.theta3);
theta4_sol = double(solutions.theta4);
for i = 1:length(theta2_sol)
theta2_val = theta2_sol(i);
theta3_val = theta3_sol(i);
theta4_val = theta4_sol(i);
% 计算误差
x_calc = L4 * cosd(apha1) + L3 * cosd(apha1 + theta4_val) + L2 * cosd(theta2_val);
z_calc = L1 + L4 * sind(apha1) + L3 * sind(apha1 + theta4_val) + L2 * sind(theta2_val);
% 计算误差
error = sqrt((x_calc - x_target)^2 + (z_calc - z_target)^2);
% 更新最优解
if error < min_error
min_error = error;
best_theta = [0, theta2_val, theta3_val, theta4_val, 0, 0];
end
end
end
C_theta1= [0, 0,theta2_val, theta3_val, theta4_val-90, 0, 0];
T_result = eye(4); % 初始化结果为单位矩阵
for i = 1:6
T = [cosd(C_theta1(i+1)), -sind(C_theta1(i+1)), 0, C_a(i);
sind(C_theta1(i+1))*cosd(C_alpha(i)), cosd(C_theta1(i+1))*cosd(C_alpha(i)), -sind(C_alpha(i)), -sind(C_alpha(i))*C_d(i+1);
sind(C_theta1(i+1))*sind(C_alpha(i)), cosd(C_theta1(i+1))*sind(C_alpha(i)), cosd(C_alpha(i)), cosd(C_alpha(i))*C_d(i+1);
0, 0, 0, 1]; % 根据给定的公式计算 T[i]
T_result = T_result * T; % 乘以每个 T[i]
end
%% 输出结果
if isempty(best_theta)
fprintf('无法找到满足条件的解。\n');
else
fprintf('最优解:\n');
fprintf('theta1: %.2f\n', best_theta(1));
fprintf('theta2: %.2f\n', best_theta(2));
fprintf('theta3: %.2f\n', best_theta(3));
fprintf('theta4: %.2f\n', best_theta(4));
fprintf('theta5: %.2f\n', best_theta(5));
fprintf('theta6: %.2f\n', best_theta(6));
fprintf('最小误差: %.2f\n', min_error);
fprintf('x_calc: %.2f\n', x_calc);
fprintf('z_calc: %.2f\n', z_calc);
disp('T_result 矩阵:');
disp(T_result);
disp('T_target 矩阵:');
disp(T_target);
end
成功的代码,验证了一下效果很好
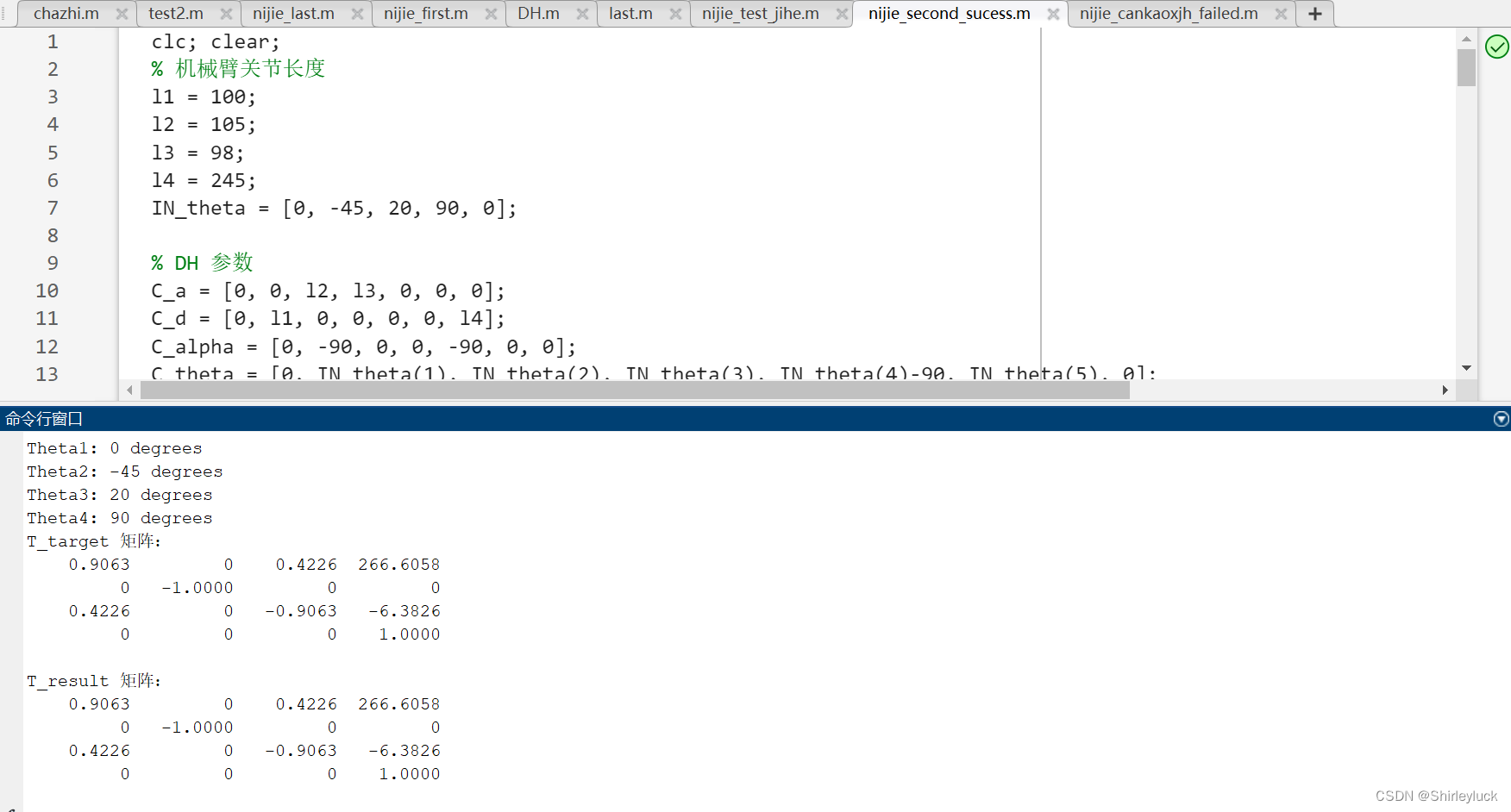
clc; clear;
% 机械臂关节长度
l1 = 100;
l2 = 105;
l3 = 98;
l4 = 245;
IN_theta = [0, -45, 20, 90, 0];
% DH 参数
C_a = [0, 0, l2, l3, 0, 0, 0];
C_d = [0, l1, 0, 0, 0, 0, l4];
C_alpha = [0, -90, 0, 0, -90, 0, 0];
C_theta = [0, IN_theta(1), IN_theta(2), IN_theta(3), IN_theta(4)-90, IN_theta(5), 0];
T_target = eye(4); % 初始化结果为单位矩阵
for i = 1:6
T = [cosd(C_theta(i+1)) -sind(C_theta(i+1)) 0 C_a(i-1+1);
sind(C_theta(i+1))*cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*cosd(C_theta(i+1)) -sind(C_alpha(i-1+1)) -sind(C_alpha(i-1+1))*C_d(i+1);
sind(C_theta(i+1))*sind(C_alpha(i-1+1)) cosd(C_theta(i+1))*sind(C_alpha(i-1+1)) cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*C_d(i+1);
0 0 0 1]; % 根据给定的公式计算T[i]
T_target = T_target * T; % 乘以每个T[i]
end
C_theta1 = calculate_joint_angles(T_target(1, 4), T_target(2, 4), T_target(3, 4));
T_result = eye(4); % 重新初始化结果为单位矩阵
for i = 1:6
T = [cosd(C_theta1(i+1)) -sind(C_theta1(i+1)) 0 C_a(i-1+1);
sind(C_theta1(i+1))*cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*cosd(C_theta1(i+1)) -sind(C_alpha(i-1+1)) -sind(C_alpha(i-1+1))*C_d(i+1);
sind(C_theta1(i+1))*sind(C_alpha(i-1+1)) cosd(C_theta1(i+1))*sind(C_alpha(i-1+1)) cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*C_d(i+1);
0 0 0 1]; % 根据给定的公式计算T[i]
T_result = T_result * T; % 乘以每个T[i]
end
disp('T_target 矩阵:');
disp(T_target);
disp('T_result 矩阵:');
disp(T_result);
function C_theta1 = calculate_joint_angles(x, y, z)
% 机械臂关节长度
l1 = 100;
l2 = 105;
l3 = 98;
l4 = 245;
% 计算 theta1
theta1 = atan2(y, x);
% 在 x-y 平面投影中的半径
r = sqrt(x^2 + y^2);
% 初始化找到解的标志
found_solution = false;
% 循环尝试不同的 a 值
for a_deg = -90:90
a = deg2rad(a_deg);
% 计算 xc 和 zc
xc = r - cos(a) * l4;
zc = z - sin(a) * l4;
% 计算 lac_sq
lac_sq = xc^2 + (zc - l1)^2;
% 检查是否在范围内
if lac_sq > (l2 + l3)^2 || lac_sq < (l2 - l3)^2
continue;
end
% 计算 jbac 和 jcac_prime
jbac = acos((l2^2 + lac_sq - l3^2) / (2 * l2 * sqrt(lac_sq)));
jcac_prime = atan2(zc - l1, xc);
% 计算 theta2
theta2 = -jbac - jcac_prime;
% 计算 theta3
theta3 = pi - acos((l2^2 + l3^2 - lac_sq) / (2 * l2 * l3));
% 检查是否有虚数部分
if isreal(theta2) && isreal(theta3)
% 计算 theta4
theta4 = - theta2 - theta3 - a;
% 标记已找到解
found_solution = true;
break; % 结束循环
end
end
if found_solution
% 返回关节角度数组
C_theta1 = [0, rad2deg(theta1), rad2deg(theta2), rad2deg(theta3), rad2deg(theta4)-90, 0, 0];
disp(['Theta1: ', num2str(rad2deg(theta1)), ' degrees']);
disp(['Theta2: ', num2str(rad2deg(theta2)), ' degrees']);
disp(['Theta3: ', num2str(rad2deg(theta3)), ' degrees']);
disp(['Theta4: ', num2str(rad2deg(theta4)), ' degrees']);
else
disp('找不到合适的逆解');
C_theta1 = NaN(1, 7); % 返回 NaN 表示未找到解
end
end
加入插值之后用于机械臂画直线的代码:
clc;clear;
%%根据起始点和末端点插值
% 定义起始点和终止点
startPoint = [280, 0, 371];
endPoint = [252, 0, 404];
% 定义插值点的数量
numPoints = 11;
% 使用 linspace 生成插值点
xValues = linspace(startPoint(1), endPoint(1), numPoints);
yValues = linspace(startPoint(2), endPoint(2), numPoints);
zValues = linspace(startPoint(3), endPoint(3), numPoints);
% 存储插值点的坐标
interpolatedPoints = [xValues; yValues; zValues]';
params = [xValues; yValues; zValues];
% 调用函数计算关节角度
results = calculate_joint_angles(interpolatedPoints);
function results = calculate_joint_angles(params)
% 初始化角度
theta1 = 0;
theta2 = 0;
theta3 = 0;
theta4 = 0;
% 机械臂关节长度
l1 = 153;
l2 = 105;
l3 = 98;
l4 = 173;
% 初始化结果数组
num_points = size(params, 1);
results = zeros(num_points, 4);
for i = 1:num_points
x = params(i, 1);
y = params(i, 2);
z = params(i, 3);
% 计算 theta1
theta1 = atan2(y, x);
% 在 x-y 平面投影中的半径
r = sqrt(x^2 + y^2);
% 初始化找到解的标志
found_solution = false;
% 循环尝试不同的 a 值
for a_deg = -90:90
a = deg2rad(a_deg);
% 计算 xc 和 zc
xc = r - cos(a) * l4;
zc = z - sin(a) * l4;
% 计算 lac_sq
lac_sq = xc^2 + (zc - l1)^2;
% 检查是否在范围内
if lac_sq > (l2 + l3)^2 || lac_sq < (l2 - l3)^2
continue;
end
% 计算 jbac 和 jcac_prime
jbac = acos((l2^2 + lac_sq - l3^2) / (2 * l2 * sqrt(lac_sq)));
jcac_prime = atan2(zc - l1, xc);
% 计算 theta2
theta2 = -jbac - jcac_prime;
% 计算 theta3
theta3 = pi - acos((l2^2 + l3^2 - lac_sq) / (2 * l2 * l3));
% 检查是否有虚数部分
if isreal(theta2) && isreal(theta3)
% 计算 theta4
theta4 = -a - theta2 - theta3;
% 保存计算结果
results(i, :) = [rad2deg(theta1), rad2deg(theta2)+180, rad2deg(theta3)+135, rad2deg(theta4)+135];
%180,135是使机械臂处于正的初始位置(正水平放置)的舵机的角度
% 标记已找到解
found_solution = true;
break; % 结束循环
end
end
% 如果没有找到解,提示错误
if ~found_solution
error(['No valid solution found for point ', num2str(i)]);
end
end
% 输出结果
disp('Calculated Joint Angles (in degrees):');
disp(results);
end