马尔可夫决策过程
马尔可夫过程
已知过往的过程为:
h t = { s 1 , s 2 , s 3 , . . . . . s t } h_t = \{s_1,s_2,s_3,.....s_t\} ht={
s1,s2,s3,.....st}
那具备马尔可夫性的状态有如下性质:
p ( s t + 1 ∣ s t ) = p ( s t + 1 ∣ h t ) p ( s t + 1 ∣ s t , a t ) = p ( s t + 1 ∣ h t , a t ) \begin{aligned} p(s_{t+1}|s_{t}) &= p(s_{t+1}|h_t)\\ p(s_{t+1}|s_t,a_t) &= p(s_{t+1}|h_t,a_t) \end{aligned} p(st+1∣st)p(st+1∣st,at)=p(st+1∣ht)=p(st+1∣ht,at)
状态转移矩阵为:
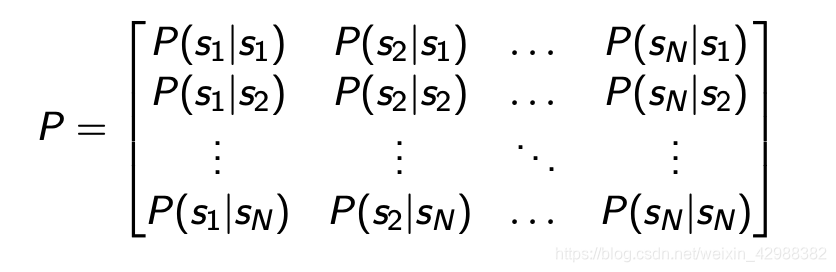
马尔可夫奖励过程(MRP)
MRP是马尔可夫链+reward
MRP的定义为:
- S是一个有限状态的集合;
- P是一个动态转移的概率模型 P ( S t + 1 = s ′ ∣ s t = s ) P(S_{t+1} = s'|s_t = s) P(St+1=s′∣st=s)
- R是一个奖励函数 R ( s t = s ) = E [ r t ∣ s t = s ] R(s_{t} = s) = \mathbb{E}[r_t|s_t = s] R(st=s)=E[rt∣st=s]
- 折扣因子 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1]
如果状态有限,R就是一个向量
MRP的例子:
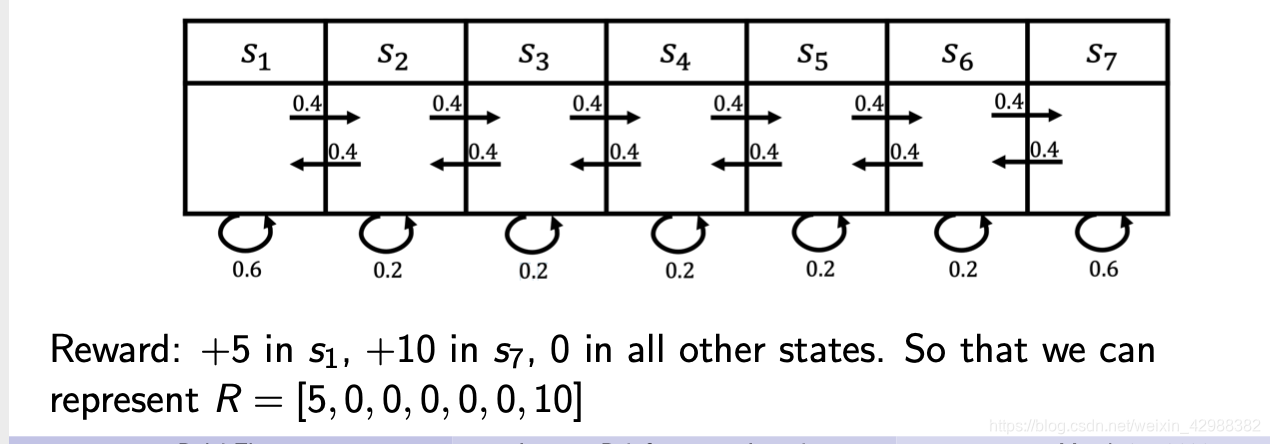
关于 r t r_t rt和 R R R的理解:首先看到 R R R是对 t t t求期望,故它是一个关于状态的函数,与时间无关。所以 r r r是一个随机过程, r t r_t rt是一个随机变量,我们通常说的reward指的是 R R R。
值函数
关于回报的定义(return):从t时刻起,到一个epsiode结束的折扣累积奖励,用 G t G_t Gt来表示:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . . . + γ T − t − 1 R T G_t = R_{t+1} + \gamma R_{t+2} + {\gamma}^2R_{t+3}+.....+{\gamma}^{T-t-1}R_{T} Gt=Rt+1+γRt+2+γ2Rt+3+.....+γT−t−1RT
注: R t R_t Rt是随机变量, R R R不是!
对于MRP过程的值函数的定义为:
V t ( s ) = E [ G t ∣ s t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . . . + γ T − t − 1 R T ∣ s t = s ] \begin{aligned} V_t(s) &= \mathbb{E}[G_t|s_t = s]\\ &= \mathbb{E}[R_{t+1} + \gamma R_{t+2} + {\gamma}^2R_{t+3}+.....+{\gamma}^{T-t-1}R_{T}|s_t = s] \end{aligned} Vt(s)=E[Gt∣st=s]=E[Rt+1+γRt+2+γ2Rt+3+.....+γT−t−1RT∣st=s]
由表达式可知, G t G_t Gt是一个随机变量, V t ( s ) V_t(s) Vt(s)是一个关于 t t t和 s s s的二元函数,代表了在当前时刻 t t t当前状态 s s s下的 G t G_t Gt的期望,是一个标量,故它会随着时间和状态都发生改变,值函数的大小也反映了在当前时间点当前状态下的能获得的预期奖励的大小。(这个期望是对 G t G_t Gt这个随机变量的分布进行积分。)
MRP的例子:
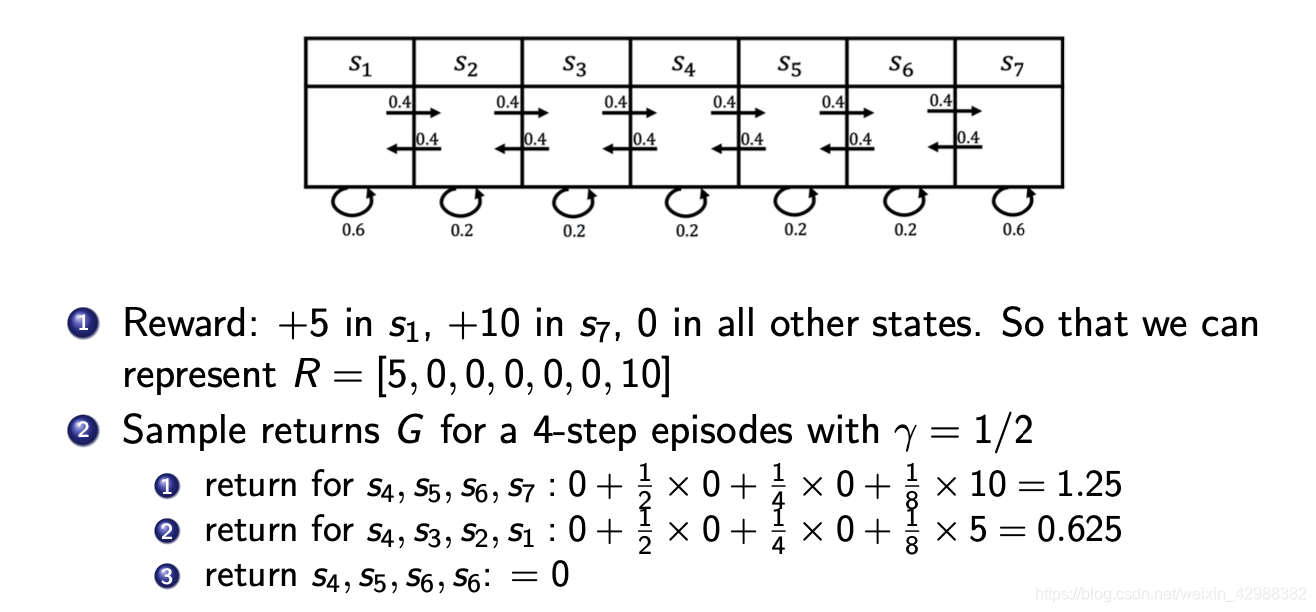
从上面的例子可以看出,因为 G t G_t Gt是一个关于 t t t的随机变量,故在不同的时间点,从同一个状态出发的回报(return) G t G_t Gt是不同的,并且会随着时间步的长短和 γ \gamma γ的大小发生较大变化。
MRP的贝尔曼方程(Bellman equation):
通过价值函数的定义可以得到以下递推式:
V ( s ) = R ( s ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V ( s ′ ) V(s) = R(s) + \gamma \sum_{s'\in S} P(s'|s)V(s') V(s)=R(s)+γs′∈S∑P(s′∣s)V(s′)
证明:先引入一个引理:期望的和等和的期望。
E [ X + Y ∣ S ] = ∬ ( x + y ) f ( x , y ∣ s ) d x d y = ∬ x f ( x , y ∣ s ) d x d y + ∬ y f ( x , y ∣ s ) d x d y = ∫ x f X ( x ∣ s ) d x + ∫ y f Y ( y ∣ s ) d y = E [ X ∣ S ] + E [ Y ∣ S ] \begin{aligned} E[X+Y|S] &= \iint(x+y)f(x,y|s)dxdy \\ &=\iint x f(x,y|s)dxdy + \iint yf(x,y|s)dxdy \\ &=\int xf_X(x|s)dx +\int yf_Y(y|s)dy\\ & = E[X|S] + E[Y|S] \end{aligned} E[X+Y∣S]=∬(x+y)f(x,y∣s)dxdy=∬xf(x,y∣s)dxdy+∬yf(x,y∣s)dxdy=∫xfX(x∣s)dx+∫yfY(y∣s)dy=E[X∣S]+E[Y∣S]
所以
V ( s ) = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . . . + γ T − t − 1 R T ∣ s t = s ] = E [ R t + 1 ∣ s t = s ] + γ E [ G t + 1 ∣ s t = s ] V(s) = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + {\gamma}^2R_{t+3}+.....+{\gamma}^{T-t-1}R_{T}|s_t = s] \\ = \mathbb{E}[R_{t+1}|s_t = s] +\gamma\mathbb{E}[G_{t+1}|s_t = s] V(s)=E[Rt+1+γRt+2+γ2Rt+3+.....+γT−t−1RT∣st=s]=E[Rt+1∣st=s]+γE[Gt+1∣st=s]
通过前述可知, G t G_t Gt是由 R t R_t Rt求和而成,由定义式知 G t + 1 G_{t+1} Gt+1在这里并没有马尔可夫性。( G t = R t + 1 + γ R t + 2 . . . . G_t=R_{t+1} + \gamma R_{t+2}.... Gt=Rt+1+γRt+2....)
故
E [ G t + 1 ∣ s t = s ] = E [ G t + 1 ] = ∑ P ( s ′ ∣ s ) E [ G t + 1 ∣ s t + 1 = s ′ ] \mathbb{E}[G_{t+1}|s_t = s] = \mathbb{E}[G_{t+1}] = \sum P(s'|s)\mathbb{E}[G_{t+1}|s_{t+1} = s'] E[Gt+1∣st=s]=E[Gt+1]=∑P(s′∣s)E[Gt+1∣st+1=s′]
我们还可以把递推式写成矩阵形式:
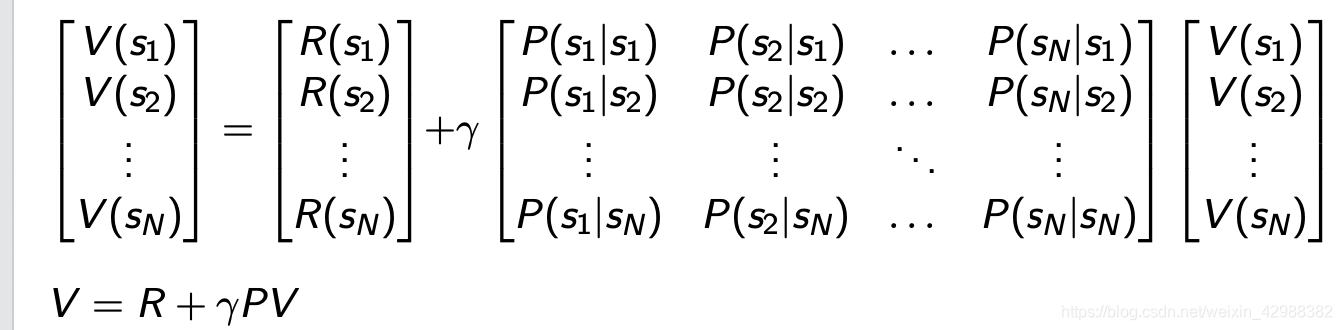
通过解上述方程便可得到V向量,但是因为复杂度过高,故一般不采用这样的方法。
迭代算法求MRP的值函数
A、蒙特卡洛算法

(这里t的含义是,当前时刻(迭代了N次以后)的值函数。)
MC方法就是通过采样求平均的方式来用期望的无偏估计平均值来代替期望。
B、迭代求解

根据MRP的贝尔曼方程一直迭代,直到值函数向量趋于稳定。
马尔可夫决策过程(MDP)
- S S S是有限状态的集合。
- A A A是有限动作的集合。
- P a P^a Pa是一个转移模型 = P ( s t + 1 = s ′ ∣ s t = s , a t = a ) P(s_{t+1} = s' | s_t = s,a_t = a) P(st+1=s′∣st=s,at=a)
MDP由(S,A,P,R, γ \gamma γ)构成。
在MDP过程中,R不仅与状态有关还与所采取的动作有关。
MDP中的Policy
Policy是在给定状态时的动作的分布。
Policy: π ( a ∣ s ) = P ( a t = a ∣ s t = s ) \pi(a|s) = P(a_t = a|s_t=s) π(a∣s)=P(at=a∣st=s)
根据Policy可以让MDP(S,A,P,R, γ \gamma γ)和policy π \pi π)与MRP过程(S, P π P^\pi Pπ, R π R^\pi Rπ, γ \gamma γ)等价:
P π ( s ′ ∣ s ) = ∑ a ∈ A π ( a ∣ s ) P ( s ′ ∣ s , a ) R π ( s ) = ∑ a ∈ A π ( a ∣ s ) R ( s , a ) P^\pi(s'|s) = \sum_{a\in A}\pi(a|s)P(s'|s,a)\\ R^\pi(s) = \sum_{a\in A}\pi(a|s)R(s,a) Pπ(s′∣s)=a∈A∑π(a∣s)P(s′∣s,a)Rπ(s)=a∈A∑π(a∣s)R(s,a)
MP/MRP过程与MDP过程的比较示意图:
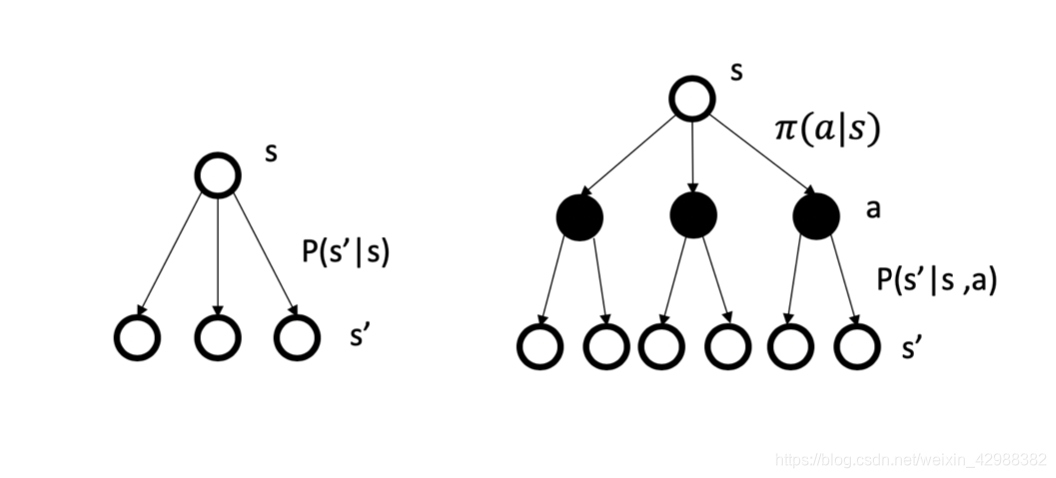
MDP还会多经历一步在动作分布上对动作的采样,从而来决定下一个状态的转移概率。
MDP的值函数
MDP中的值函数(state-value) v π ( s ) v^\pi(s) vπ(s)表示的是在状态s,policy是 π \pi π的预期回报。动作价值(action-value)函数是 q π ( s , a ) q^\pi(s,a) qπ(s,a)。
v π ( s ) = E [ G t ∣ s t = s ] q π ( s , a ) = E [ G t ∣ s t = s , A t = a ] v^\pi(s) = \mathbb{E}[G_t|s_t = s]\\ q^\pi(s,a) = \mathbb{E}[G_t|s_t = s,A_t = a] vπ(s)=E[Gt∣st=s]qπ(s,a)=E[Gt∣st=s,At=a]
v π ( s ) v^\pi(s) vπ(s)和 q π ( s , a ) q^\pi(s,a) qπ(s,a)之间的关系为:
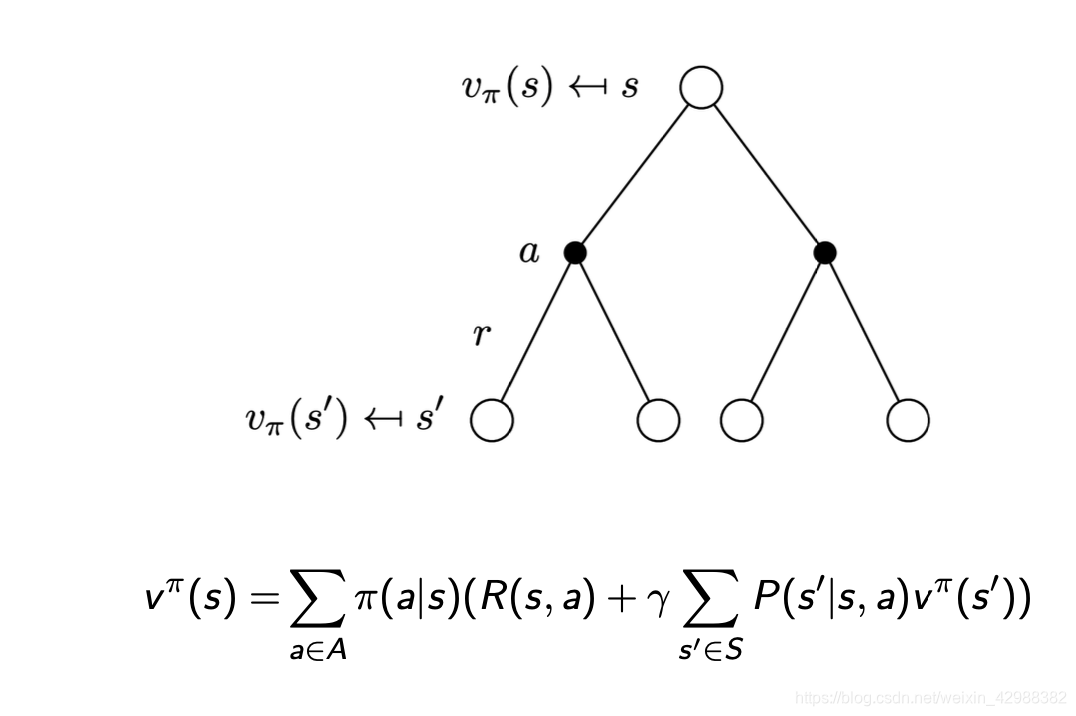
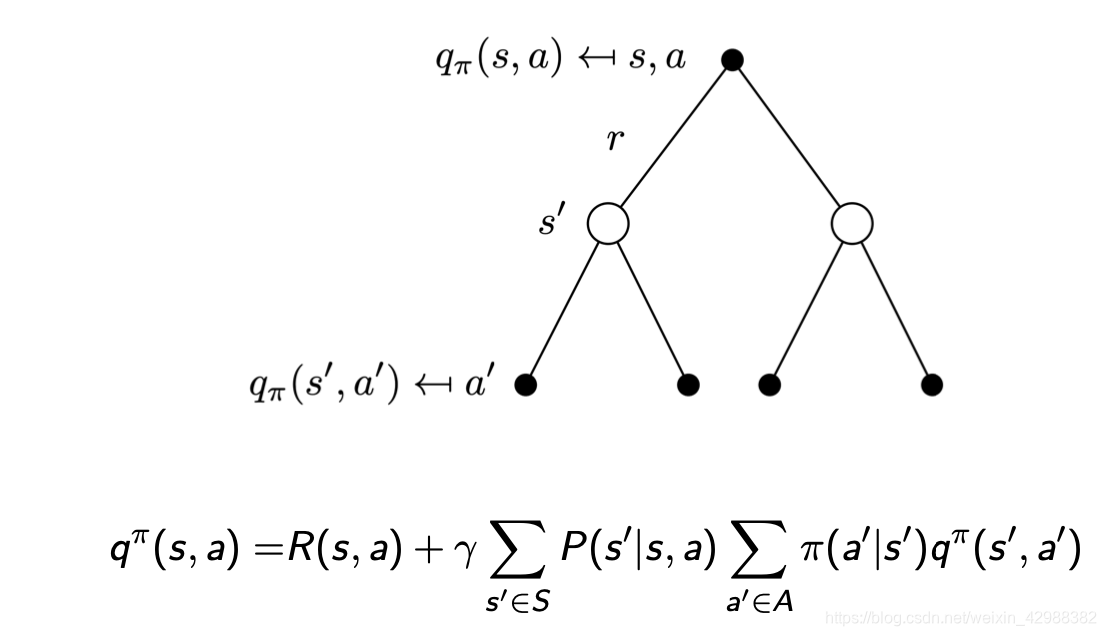
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) q π ( s , a ) q π ( s , a ) = R a s + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) v π ( s ′ ) v^\pi(s) = \sum_{a\in A} \pi(a|s)q^\pi(s,a)\\ q^\pi(s,a) = R_a^s +\gamma \sum_{s'\in S} P(s'|s,a)v^\pi(s') vπ(s)=a∈A∑π(a∣s)qπ(s,a)qπ(s,a)=Ras+γs′∈S∑P(s′∣s,a)vπ(s′)
贝尔曼期望方程
v π ( s ) = E π [ R t + 1 + γ v π ( s t + 1 ) ∣ s t = s ] q π ( s , a ) = E π [ R t + 1 + γ q π ( s t + 1 , A t + 1 ) ∣ s t = s , A t = a ] v^\pi(s) = E_\pi[R_{t+1}+\gamma v^\pi(s_{t+1})|s_t = s]\\ q^\pi(s,a) = E_\pi[R_{t+1}+\gamma q^\pi(s_{t+1},A_{t+1})|s_t = s,A_t = a] vπ(s)=Eπ[Rt+1+γvπ(st+1)∣st=s]qπ(s,a)=Eπ[Rt+1+γqπ(st+1,At+1)∣st=s,At=a]
根据之前的MRP的贝尔曼方程可以很容易的得到MDP的贝尔曼方程:
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) v π ( s ′ ) ) q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) v^\pi (s) = \sum_{a\in A}\pi(a|s)(R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)v^\pi(s')) \\ q^\pi(s,a) = R(s,a) +\gamma\sum_{s'\in S}P(s'|s,a)\sum_{a'\in A}\pi(a'|s')q^\pi(s',a') vπ(s)=a∈A∑π(a∣s)(R(s,a)+γs′∈S∑P(s′∣s,a)vπ(s′))qπ(s,a)=R(s,a)+γs′∈S∑P(s′∣s,a)a′∈A∑π(a′∣s′)qπ(s′,a′)
再从直观上理解以下上述方程表达的含义:
下图两个练习的代码附在后面:
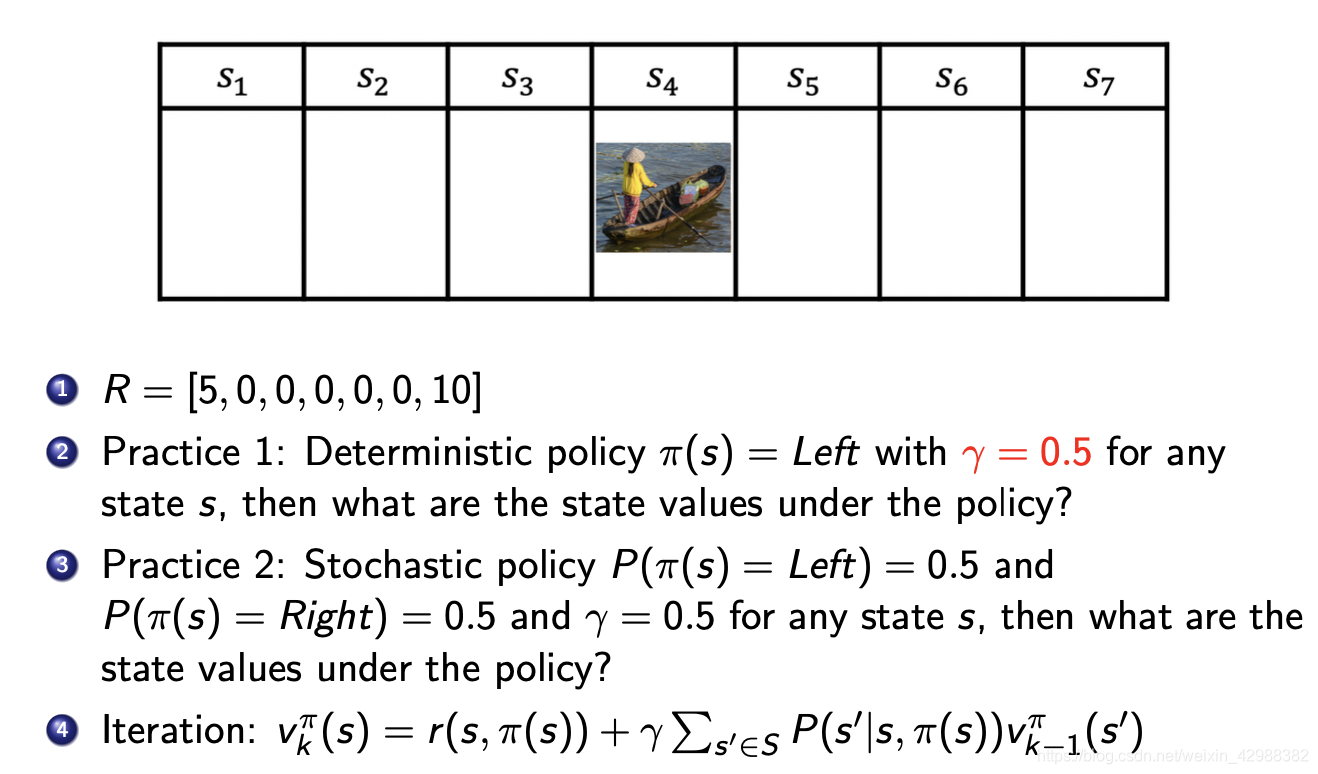
#练习1
S = list(range(7))
V1 = np.array([0,0,0,0,0,0,0])
V = np.array([999,999,999,999,999,999,999])
R = np.array([5,0,0,0,0,0,10])
epsilon = 10
gamma = 0.5
pro=np.array([[0,0,0,0,0,0,0],[1,0,0,0,0,0,0],[0,1,0,0,0,0,0],[0,0,1,0,0,0,0],
[0,0,0,1,0,0,0],[0,0,0,0,1,0,0],[0,0,0,0,0,1,0]])
#terminal_state = 0
while np.abs(V1.sum()-V.sum())>0.0001:
V = V1
for s in S:
all_sum = 0
for s_ in S:
all_sum = all_sum + pro[s][s_]*V[s_]
V1[s] = R[s] + gamma*all_sum
print(V)
#练习2
S = list(range(7))
V1 = np.array([0,0,0,0,0,0,0])
V = np.array([999,999,999,999,999,999,999])
R = np.array([5,0,0,0,0,0,10])
epsilon = 10
gamma = 0.5
pro=np.array([[0.5,0.5,0,0,0,0,0],[0.5,0,0.5,0,0,0,0],[0,0.5,0,0.5,0,0,0],[0,0.5,0,0.5,0,0,0],
[0,0,0,0.5,0,0.5,0],[0,0,0,0,0.5,0,0.5],[0,0,0,0,0,0.5,0.5]])
while np.abs(V1.sum()-V.sum())>0.0001:
V = V1
for s in S:
all_sum = 0
for s_ in S:
all_sum = all_sum + pro[s][s_]*V[s_]
V1[s] = R[s] + gamma*all_sum
print(V)
最优值函数
最优的值函数和动作值函数指的是遍历所有的policy选择能使值函数 v π ( s ) v_\pi(s) vπ(s)或者 q π ( s , a ) q_\pi(s,a) qπ(s,a)最大的策略,并将最大值作为最优值函数。
v ∗ ( s ) = max π v π ( s ) q ∗ ( s , a ) = max π q π ( s , a ) v_*(s) = \max_{\pi}v_{\pi}(s)\\ q_*(s,a) = \max_{\pi}q_{\pi}(s,a) v∗(s)=πmaxvπ(s)q∗(s,a)=πmaxqπ(s,a)
最优值函数展示了MDP的可能的最优表现。
最优policy
定义:如果对于任意状态都有 v π ( s ) > = v π ′ ( s ) v_\pi(s)>= v_{\pi'}(s) vπ(s)>=vπ′(s)那么就有, π > = π ′ \pi>=\pi' π>=π′
定理:对于任意的MDP都存在以下性质:
- 一定存在最优策略 π ∗ \pi_* π∗
- 最优策略一定能够产生最优值函数 v π ∗ ( s ) = v ∗ ( s ) v_{\pi_*}(s) = v_*(s) vπ∗(s)=v∗(s)
- 最优策略一定能产生最优的动作值函数 q π ∗ ( s , a ) = q ∗ ( s , a ) q_{\pi_*}(s,a) = q_*(s,a) qπ∗(s,a)=q∗(s,a)
最优策略可以通过最大化动作值函数来获得:
π ∗ ( a ∣ s ) = { 1 if a = argmax a ∈ A q ∗ ( s , a ) 0 otherwise \pi_{*}(a | s)=\left\{\begin{array}{ll} 1 & \text { if } a=\underset{a \in \mathcal{A}}{\operatorname{argmax}} q_{*}(s, a) \\ 0 & \text { otherwise } \end{array}\right. π∗(a∣s)={
10 if a=a∈Aargmaxq∗(s,a) otherwise
注:对于任意的MDP一定存在一个最优的决定性的policy。
MDP问题中的预测和控制
1、prediction:
- 输入:MDP < S , A , P , R , γ > <S,A,P,R,\gamma> <S,A,P,R,γ>和ploicy π \pi π或者写成 < S , P π , R π , γ > <S,P^\pi,R^\pi,\gamma> <S,Pπ,Rπ,γ>
- 输出:价值函数 v π v^\pi vπ
2、control:
- 输入:MDP < S , A , P , R , γ > <S,A,P,R,\gamma> <S,A,P,R,γ>
- 输出:最优的值函数 v ∗ v^* v∗和最优的policy π ∗ \pi^* π∗
以上两个问题都可以用动态规划来解决。因为原问题可以被递归分解成多个子问题,故若达到全局最优,那在任一子问题上也是最优。