深度强化学习第2课｜马尔可夫决策过程

0 写在前面

材料源自某高校课程ppt，恕不共享

1 简介

马尔可夫决策过程(Markov Decision Processes, MDP) 是RL中的一个基本理论，它为RL较为公式化地描述了一个environment(以下简称env)，这个env比较理想化，是fully observable(即环境的所有变化对智能体agent可见)。
值得一提的是，所有RL问题都可以是MDP问题：

• Optimal control primarily deals with continuous MDPs
• Partially observable problems can be converted into MDPs
• Bandits(老虎机问题) are MDPs with one state

2 马尔可夫属性

MDP形式上类似数字电路中的状态机，即状态的转换过程，能够构成MDP的状态称之为具有马尔可夫属性，以下简称M属性。定义如下：

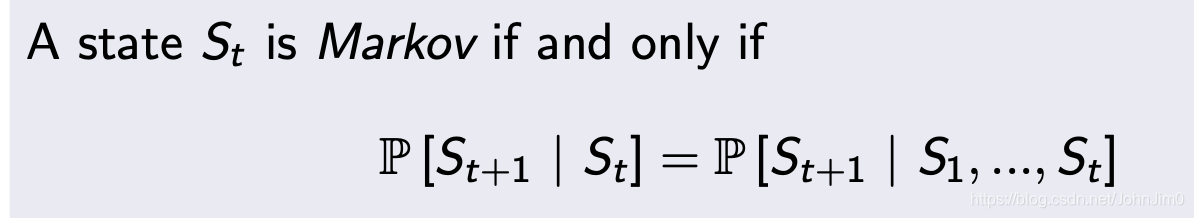
上述的数学含义是 $S_{t+1}$在 $S_t$下的条件概率与在 $S_1,S_2,...,S_t$并集下的概率相等，即The future is independent of the past given the present(未来的状态只与当前状态有关)。

3 State Transition Matrix

在MDP中，当前状态可以在下一步转换到自身状态，也可能转换到其他状态，例如总共3个状态，处于状态1即 $s_1$时，转到自身或其他状态 $s_2$和 $s_3$的概率分别是0.2，0.4，0.4，注意这里的概率和自然等于1。这种转换过程需要用state transition probability来描述：

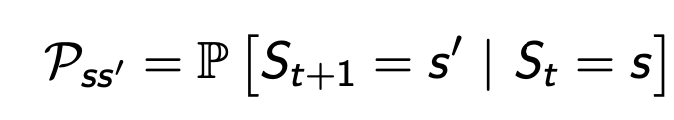
即状态为 $s$条件下，下一步状态为 $s'$的概率。
对于n个状态的情况下，把每个state transition probability凑到一起就成了State Transition Matrix：

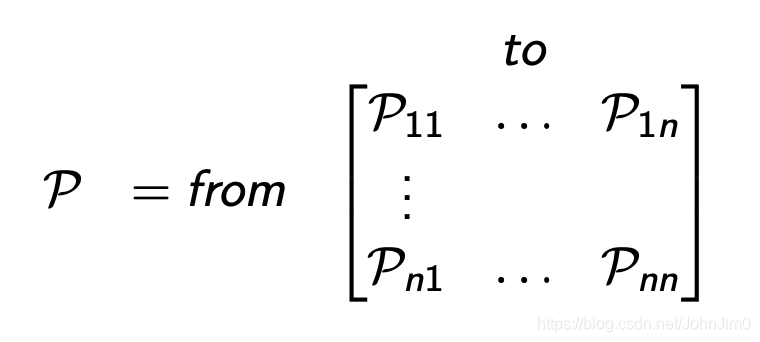
忽略图中的from和to(懒得改了)，其中根据上面转换到所有状态的概率和为1，矩阵每行的元素之和也等于1。

4 MP

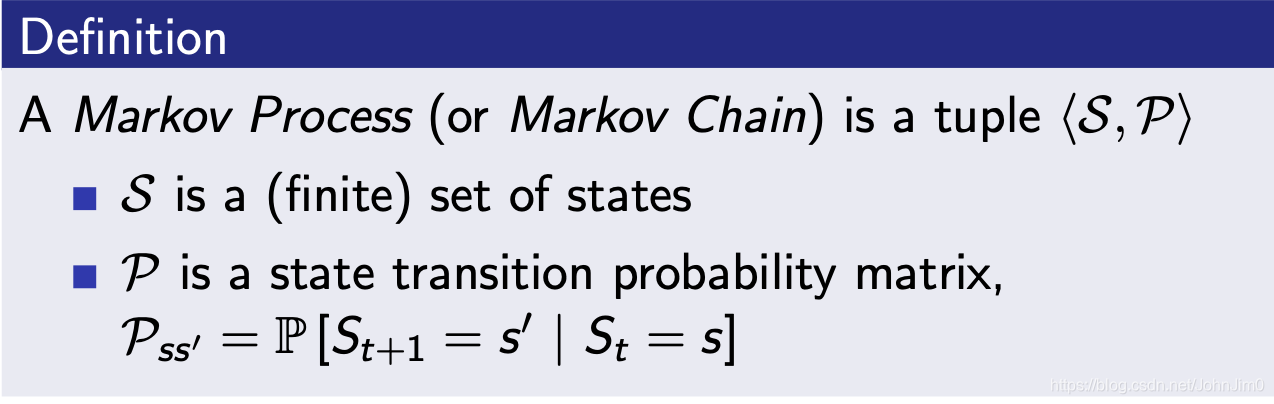
马尔可夫过程(MP)是一个无记忆的随机过程：

5 示例：Student Markov Chain

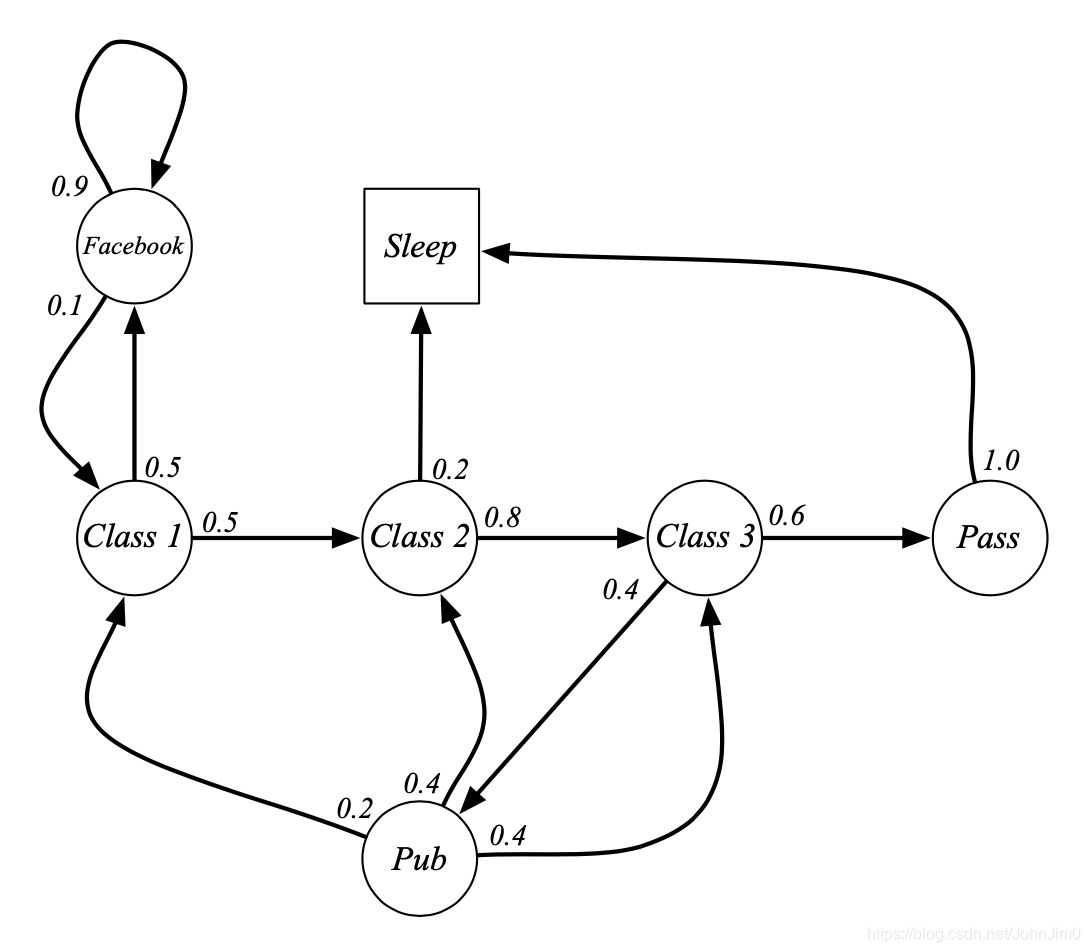
如图是一个学生状态的马尔可夫过程或者说马尔可夫链，图中的意思是，假如学生在上class 1，那么结束class 1后有0.5的概率继续上class 2，也有0.5的概率会去刷facebook，注意这里有一个终止状态，即sleep，进入sleep之后不再跳转，也如定义中所说的 $S$是一个(finite) set of states。
假设我们的初始状态是class 1(C1)，它最终是会进入终止状态sleep(当前也可能不会而变成一个循环状态)的，可能的情况有很多种：

• C1 C2 C3 Pass Sleep
• C1 FB FB C1 C2 Sleep
• C1 FB FB C1 C2 C3 Pub C1 FB FB FB C1 C2 C3 Pub C2 Sleep
  这里的每一种情况一般称为一个回合(episode)。那么这里我们就可以描述它的 State Transition Matrix了，如下：
  

6 Markov Reward Process

仅仅有上面的过程还不足以做出决策，RL本质上是一个基于reward的过程，我们需要引入reward，定义如下：

在Student Markov Chain示例中，则可以表示为：

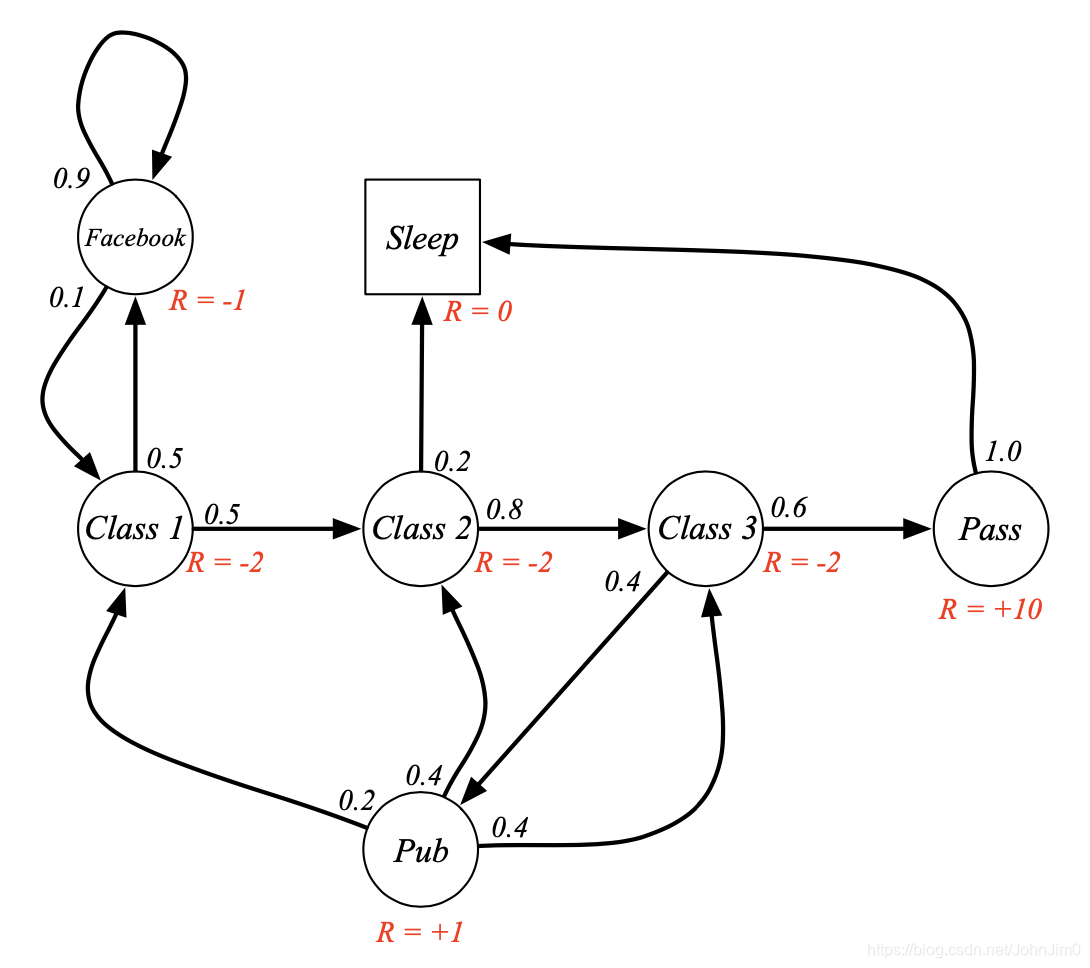
即比如当我们进入状态class 1时，就给一个-2的奖励，这个奖励可以是人为规定的。

7 Return

在一个**回合(episode)**中，我们每完成一个状态就给一个奖励，回合结束时将奖励累积起来就是最终的回报(return)，如下：

这里引入了一个衰减因子 $\gamma$，它在0-1范围之间，它的基本意义如下：

8 为什么需要衰减？

大多数MDP都会有这个衰减因子，原因如下：

• 便于数学计算
• 避免循环马尔可夫过程中的return成无限大的值
• 没有衰减，未来的不确定性可能不能很好地表示出来
• If the reward is financial, immediate rewards may earn more interest than delayed rewards
• Animal/human behaviour shows preference for immediate reward

9 MRP的值函数

value function(值函数)是用来表示某个状态的长期价值的。

如下：

上面可以看出不同情况下或者说不同的episode，每个状态的value不同的，我们value function计算的是期望值，但是由于每个状态的episode很多，显然不方便直接列举计算，而贝尔曼方程给出了答案。

10 贝尔曼方程

贝尔曼方程给出了值函数的求解，

即当前状态的值 $v(s)$等于完成当前状态的奖励 $R_{t+1}$以及下一步各状态的值的衰减和的期望。

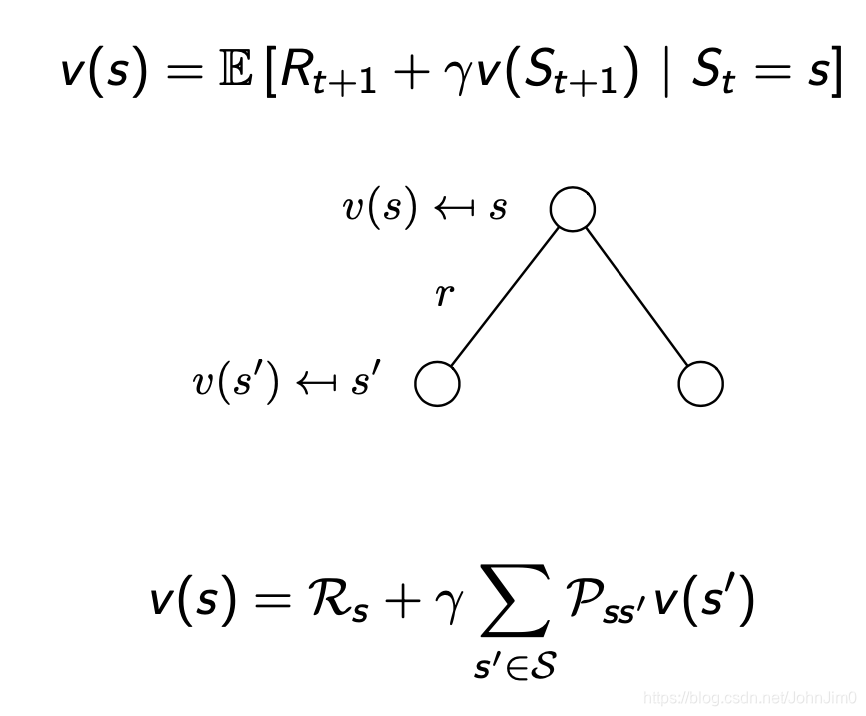
示例如下：

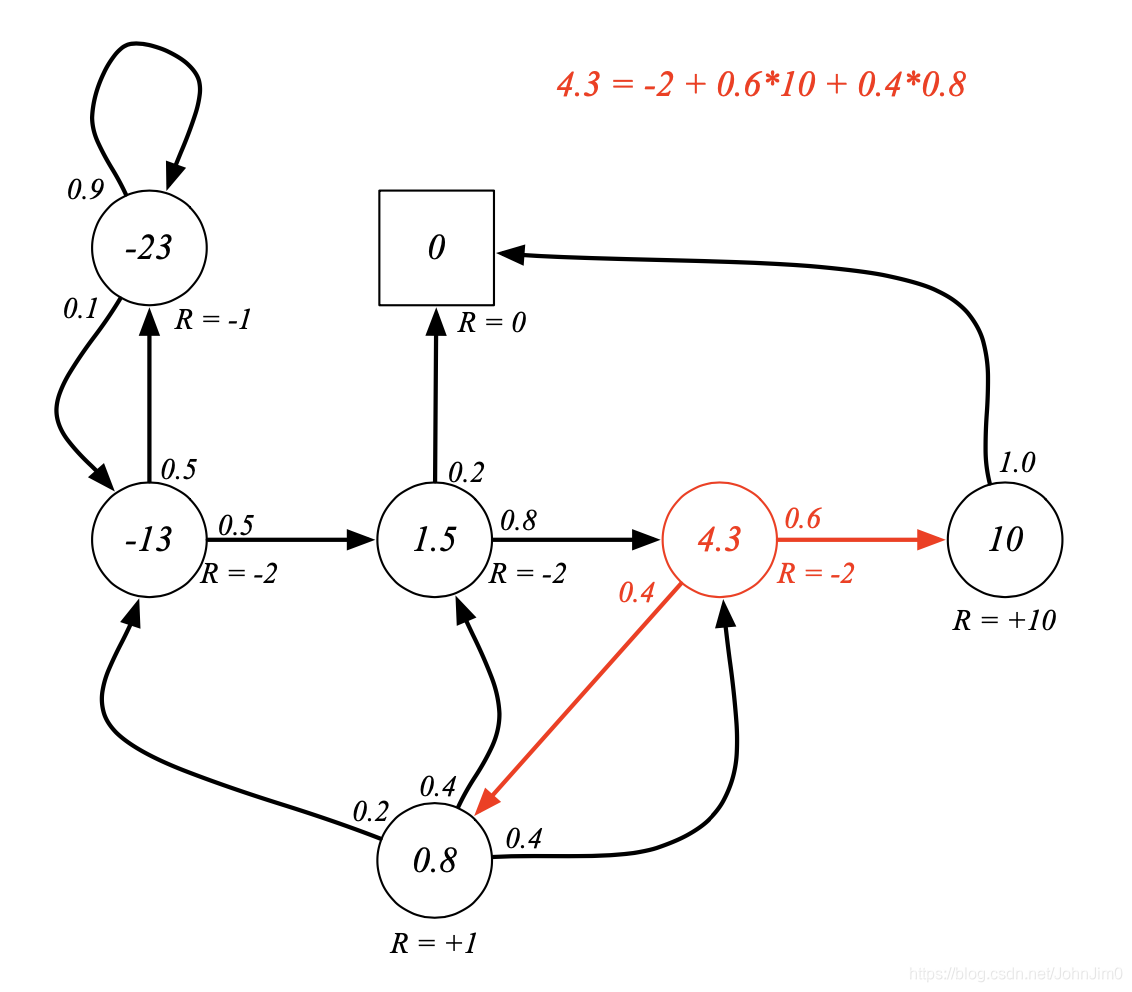
如图这里 $R_{t+1}=-2$，下一个状态有两个，对应的概率分别为0.6和0.4，值分别为10和8，注意这里的衰减因子 $\gamma=1$。
此时会产生一个问题，这里的10和8又是怎么来的呢？我们需要从终止状态算起，首先看终止状态即 $R=0$的状态，因为没有下一个状态，且 $R_{t+1}=0$，所以对应的value也等于0，然后再找与终止状态相邻并且简单的状态，即 $R=10$的那个，因为它的下一个状态只有终止状态，所以也容易得出它的value=10，计算其他的可能就需要设未知数求解了，这是笔者想到的第一个比较自然的高中数学思路，其实用矩阵表示的话计算会更加简单，也能适用于更为复杂的情况，见下一节。

11 贝尔曼方程的数学表示

根据上面一节，不难写出贝尔曼方程的矩阵表示形式，可以看到包含了所有状态之后，这里不再有 $v(s)$和 $v(S_{t+1})$的区分，而都变成了 $v$，这就是所谓的数学之美！，有了这个计算value就简单多了，如下：

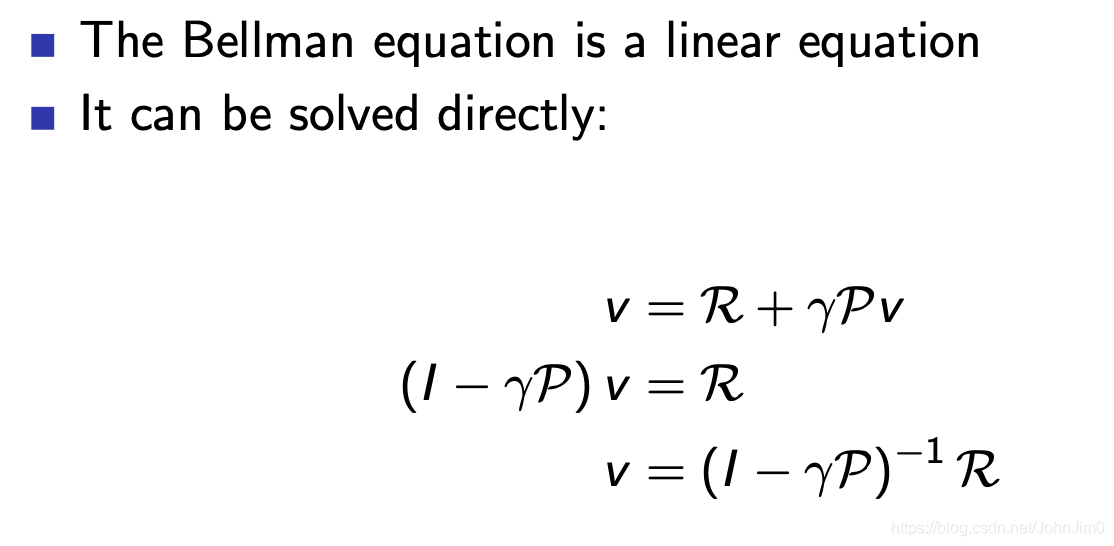
当然说简单也不简单，这里涉及到逆矩阵，对于简单的MDP可以计算得出，对于复杂的就需要用到其他各种各样的方法，比如：

• Dynamic programming
• Monte-Carlo evaluation
• Temporal-Difference learning

12 MDP

上面描述了Markov Process和Markov Reward Process，这次我们再引入一个action，就成了一个完备的MDP了，如下：

还是以学生作为示例，图中的红字就是action，注意跟状态state有区别：

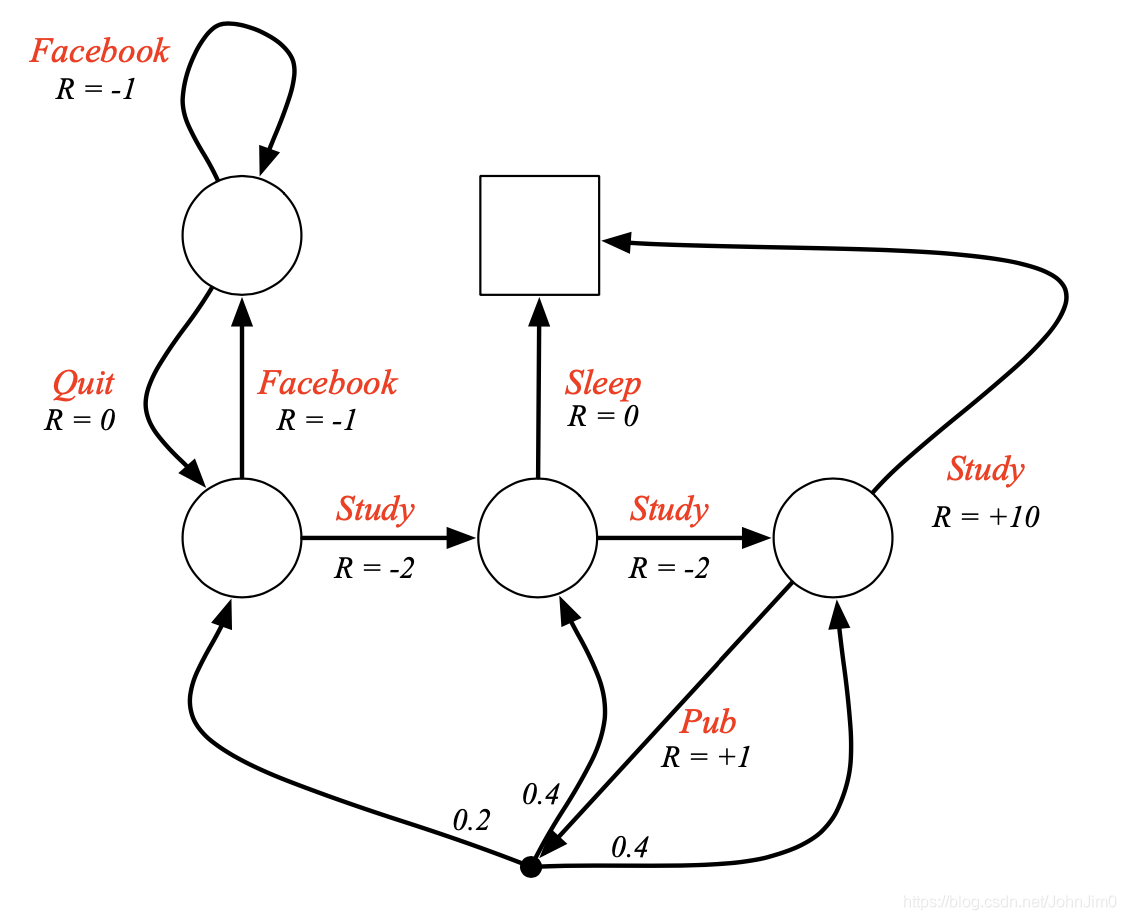
13 Policy

policy即策略，RL最终就是要找到一个最优策略来达到比如回报最大的目标，数学定义如下：

即它是状态为s条件下的a的概率分布，注意policy是描述智能体agent的行为的，它只依赖于当前的状态。
总结一下就是对于一个MDP即 $\mathcal{M}=\langle\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma\rangle$和策略 $\pi$，一个状态序列(state sequence) $S_1,S_2,...$或者说一个回合(episode)就是一个马尔可夫过程 $\left\langle\mathcal{S}, \mathcal{P}^{\pi}\right\rangle$，一个状态奖励序列 $S_1,R_2,S_2,...$就是Markov Reward Process $\left\langle\mathcal{S}, \mathcal{P}^{\pi}, \mathcal{R}^{\pi}, \gamma\right\rangle$，并且：

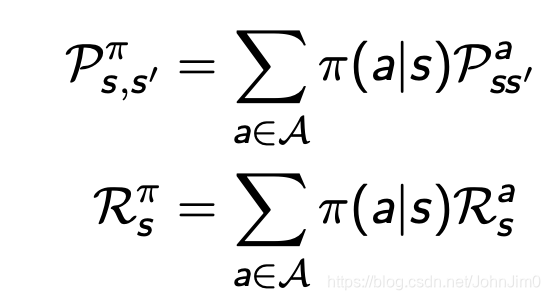
14 MDP的值函数

MDP的值函数分为状态-值函数和动作-值函数，如下：

注意v跟q的关系如下：

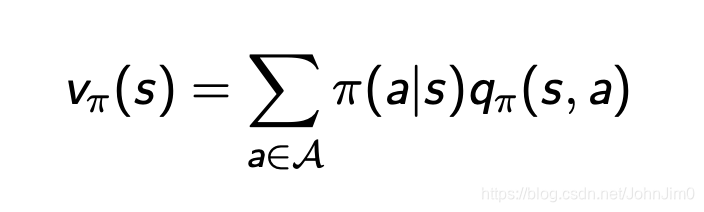
与上面MRP的值函数类似，我们依然需要用到贝尔曼方程计算每个状态的期望价值，这里使用q表示value，经典算法q-learning的q也是这个q：


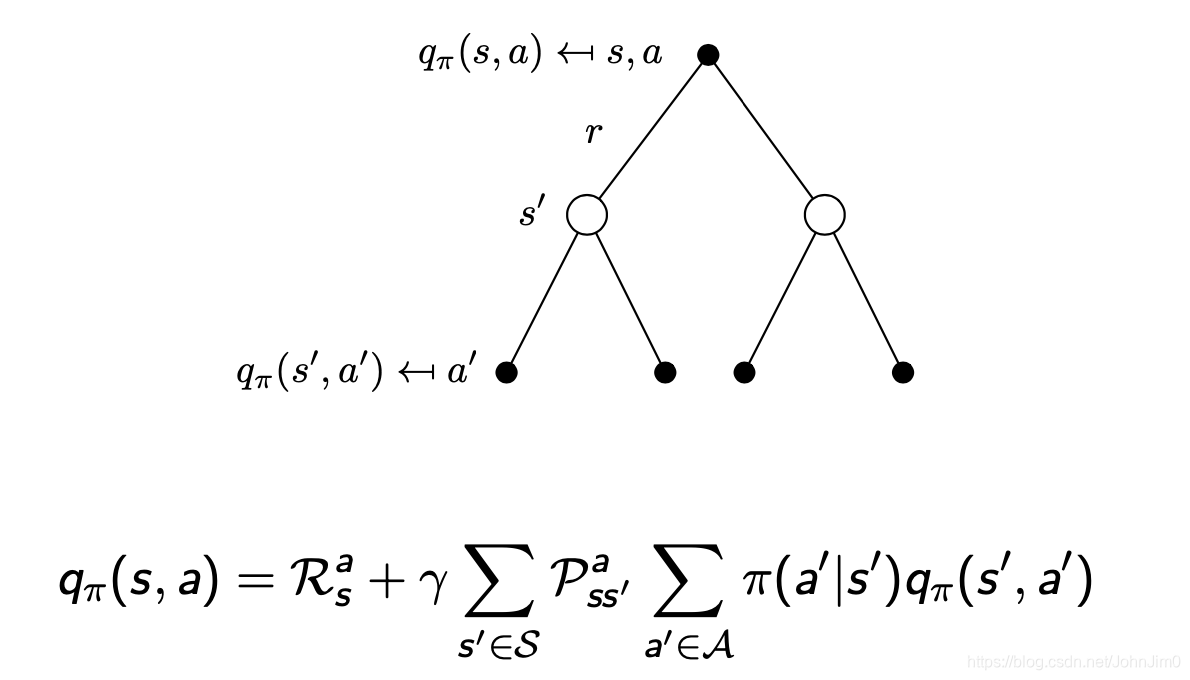
注意这里的 $\gamma$和 $\pi\left(a^{\prime} | s^{\prime}\right)$一般是常量，这里取 $\gamma=1$和7.4状态下的 $\pi\left(a^{\prime} | s^{\prime}\right)=0.5(即此状态下对study和pub动作雨露均沾，概率各为0.5)$，以学生为例：

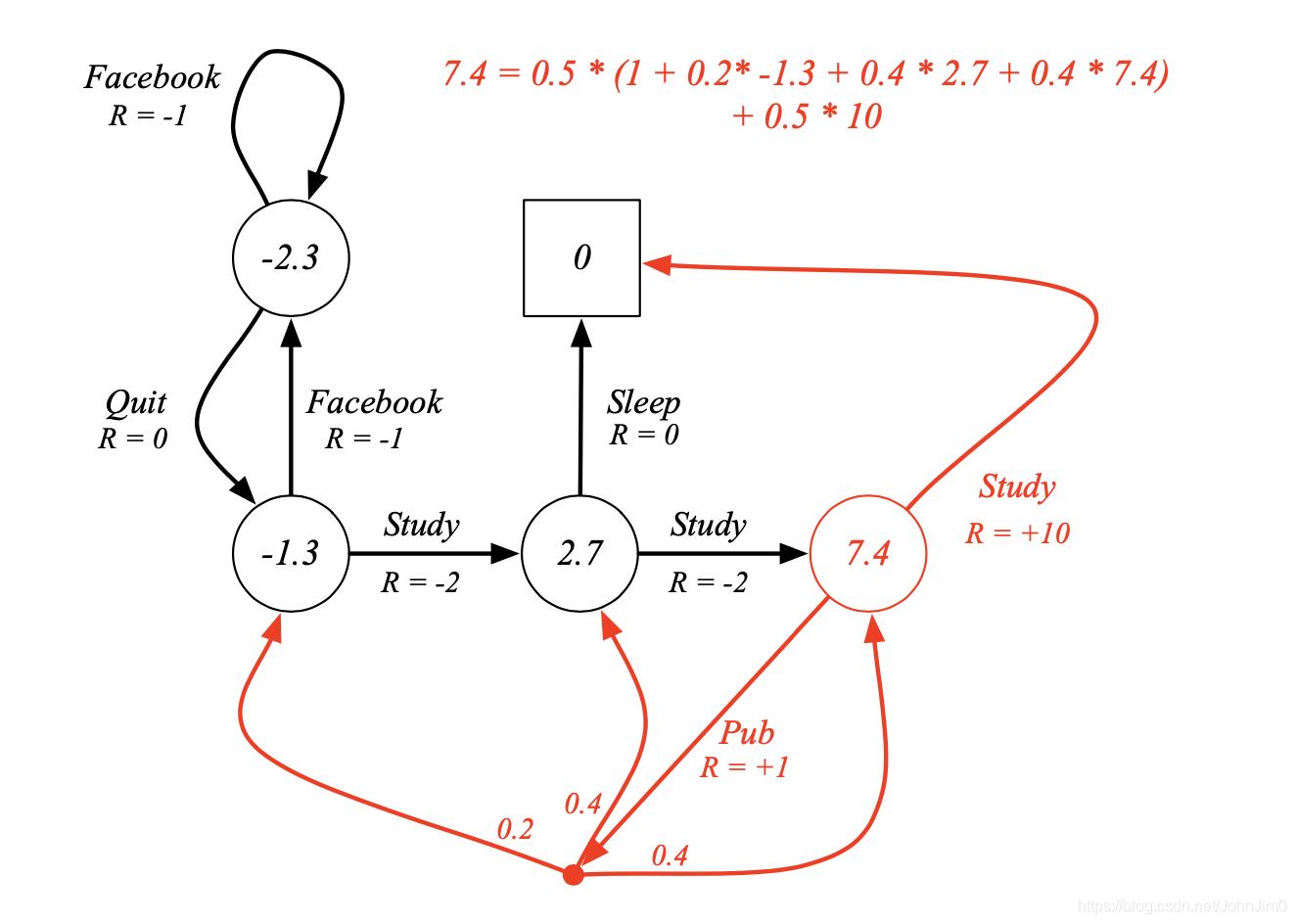
以7.4(这个是v值而不是q)这个状态为例，对于这个状态它有两种可能的行为即study和pub，study之后对应的只有0的那个状态，pub之后可能有三种状态，先计算study这个动作对应的q值，首先完成study之后对应的奖励为10，因为下一步的v值即这里的 $\sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} | s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right)$等于0，所以study对应的 $q_{\pi}(s, a)$等于10，再计算pub对应的q值，易知奖励为1，第二项 $\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} | s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right)=1*0.2*-1.3+1*0.4*2.7+1*0.4*7.4$，两个q值相加再乘以 $\pi(a | s)=0.5$即可。
前面也提到这种计算方法不适用于复杂情况，因此同样的对应的贝尔曼方程的矩阵表示如下：

15 最优值函数

我们定义最优值函数即对应的value达到最大，也是MDP的最优解。

16 最优策略

对于智能体agent我们则需要知道最优策略，最优策略即最优值函数下对应的策略，如下：

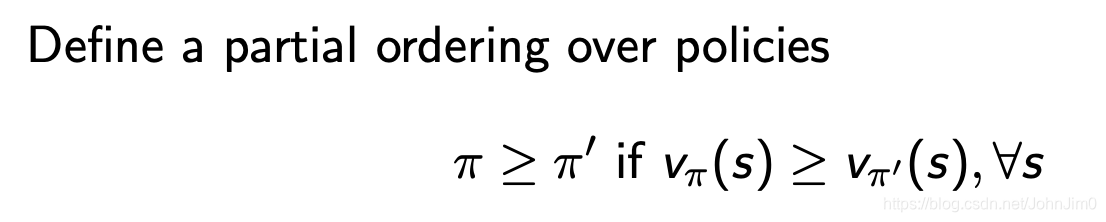
对于任意MDP，定论如下：

• 必然存在最优策略，可能不止一个
• 最优策略对应的state-value function值(简称v值)最大
• 最优策略对应的action-value function(q值)最大

17 寻找最优策略

一个简单的最优策略可以通过找到每步最大的q值得出，如下：

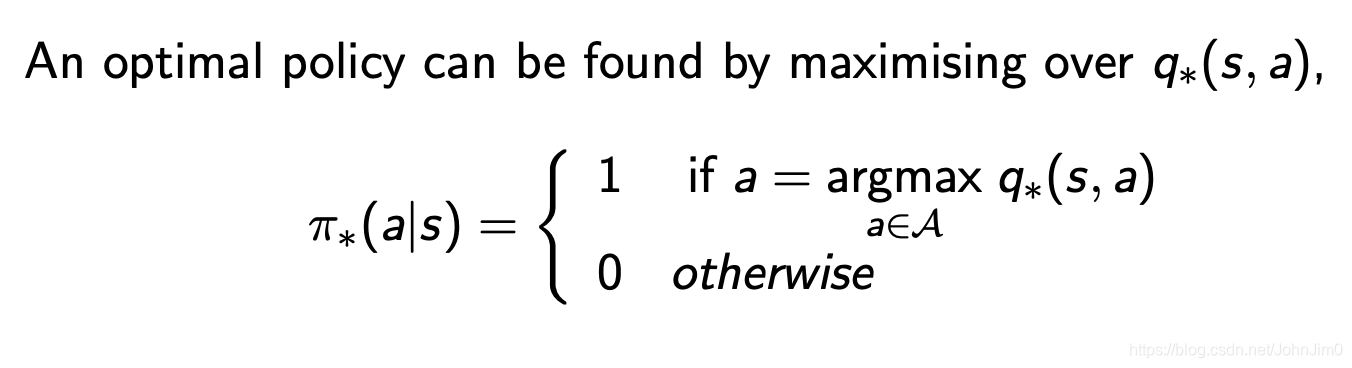
如下：

注意这里圆圈里面的值不是之前的v值而是q值，这里设facebook那里为起始状态，那么最优化策略就是图中的红线，即每次选择使q值最大的状态和动作。

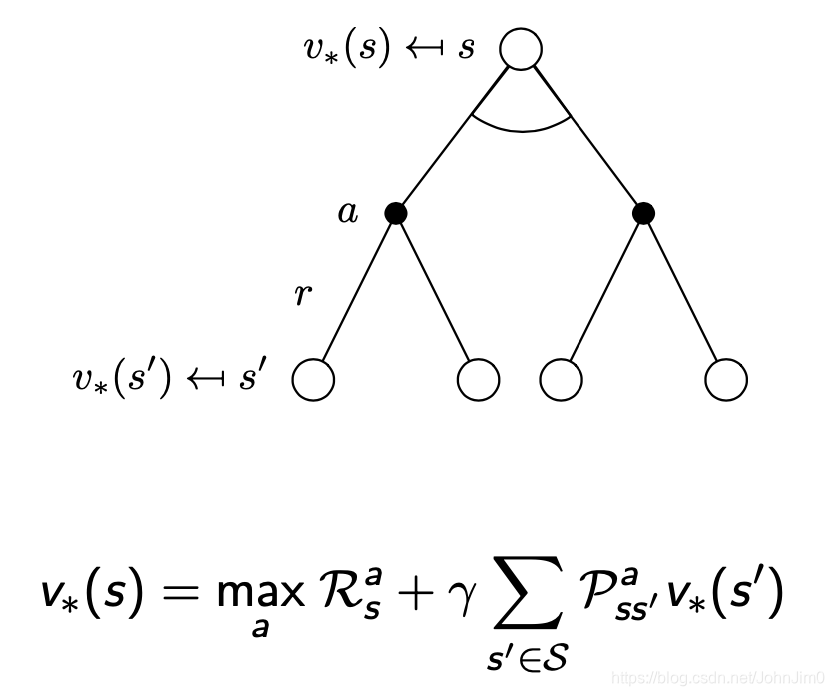
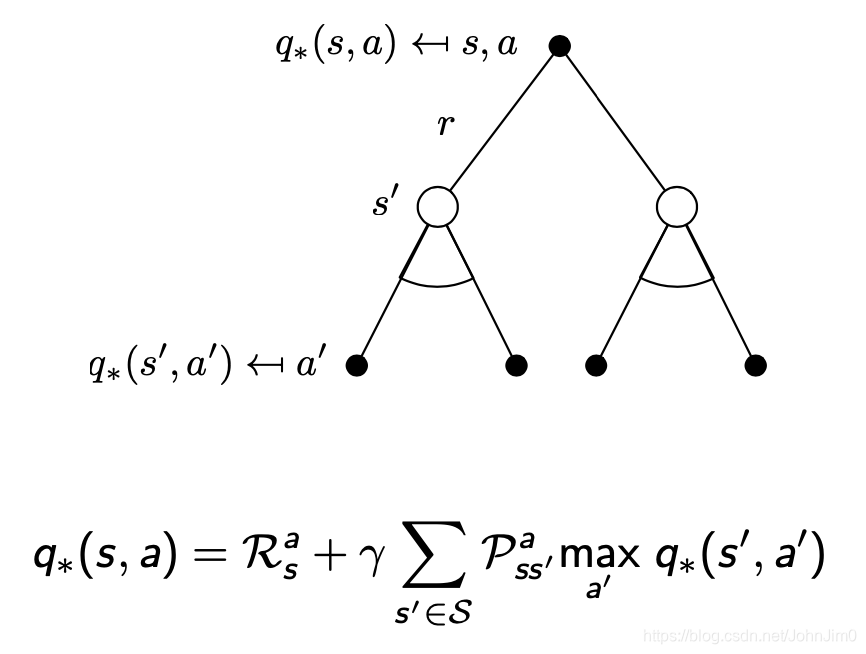
18 贝尔曼最优等式

对应的贝尔曼最优等式(Bellman Optimality Equation)表示如下：


如下：

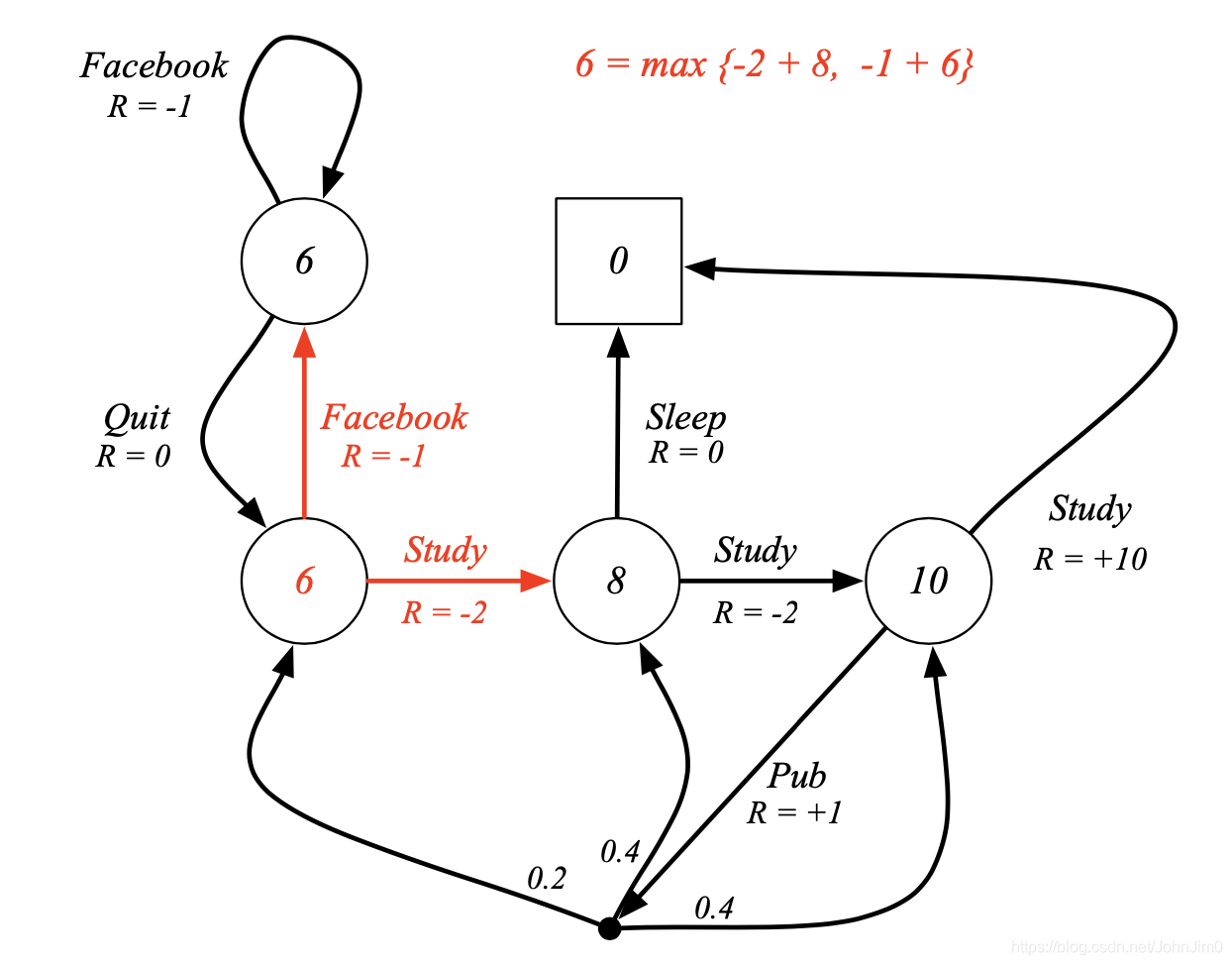
假如我们处于红色数字6的状态，对应的下一步动作有两个，每个动作对应的q值分别为-2+8=6，和-1+6=5，此时我们就应该选择q值最大的study动作。
需要注意的是贝尔曼最优等式是非线性的，因此没有一个通解，常用的解决方法如下：

• Value Iteration
• Policy Iteration
• Q-learning
• Sarsa

19 MDP的拓展

前面简介那一节说了，原始的MDP是有限个状态的，并且fully observable，而相应地MDP的拓展形式有：

• Infinite and continuous MDPs
• Partially observable MDPs
• Undiscounted, average reward MDPs

19.1 Infinite MDPs

即无限状态的MDP，可能情况以及对应的解决方法如下：

• 离散的无限状态-动作空间
  比较简单
• 连续的状态-动作空间
  Closed form for linear quadratic model (LQR)，即转换为线性二次模型
• 连续时间
  1)Requires partial differential equations，需要偏微分方程
  2)Hamilton-Jacobi-Bellman (HJB) equation
  3)Limiting case of Bellman equation as time-step → 0

19.2 POMDPs

即Partially observable MDPs，如下：

这里引入了一个观测值，即observation。
后面的暂时不展开，有兴趣可以看一下Ergodic Markov Process。