基于小波变换和OMP的图像压缩算法matlab仿真

随着数字图像技术的迅速发展，图像压缩技术在诸多领域如医学成像、遥感监测、多媒体通信等得到了广泛应用。小波变换作为一种多尺度分析工具，在图像压缩中表现出色。结合正交匹配追踪（Orthogonal Matching Pursuit, OMP）算法，可以进一步提高图像压缩的效率和重构质量。

1.小波变换原理

小波变换是一种时频分析方法，具有多分辨率分析的特点。它通过将信号分解为一系列小波系数的组合，实现了信号在不同尺度上的表示。在图像压缩中，小波变换可以有效地去除图像中的冗余信息，保留重要特征。

1.1 连续小波变换

对于一维连续信号(f(t))，其连续小波变换定义为：

扫描二维码关注公众号，回复： 17326145 查看本文章

其中，(a)为尺度因子，控制小波函数的伸缩；(b)为平移因子，控制小波函数的平移；(\psi(t))为小波基函数；(*)表示复共轭。

在实际应用中，为了计算方便，通常使用离散小波变换。

1.2 离散小波变换

离散小波变换（DiscreteWavelet Transform, DWT）和离散傅里叶变换（Discrete FourierTransform, DFT）不一样，在Matlab中确实有dwt函数，但它与一般书中讲的DWT不一样，dwt是基于Mallat（法国学者，音译为马拉特）算法实现的，针对的离散时间信号，而DWT指的是将连续小波变换（Continuous WaveletTransform, CWT）中的尺度参数a和时移参数b离散化，即将下式中的a和b离散化，但t仍然是连续的。离散小波变换通过对尺度因子和平移因子进行离散化，将连续小波变换转化为离散形式。常用的离散小波变换有二进制小波变换，其定义为：

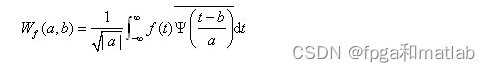
其中，(a)为尺度因子，控制小波函数的伸缩；(b)为平移因子，控制小波函数的平移；(\psi(t))为小波基函数；(*)表示复共轭。对于二维图像信号，可以通过一维小波变换的张量积形式进行扩展，得到二维小波变换。

2.OMP算法原理

OMP算法是一种贪婪算法，用于求解稀疏信号的重建问题。在图像压缩中，OMP算法可以从压缩后的观测信号中恢复出原始图像信号。OMP算法的基本思想是在每一步迭代中，从观测矩阵中选择与当前残差最相关的列，然后利用最小二乘法更新已选列对应的稀疏系数，最后更新残差。具体步骤如下：

3.基于小波变换和OMP的图像压缩算法

基于小波变换和OMP的图像压缩算法结合了小波变换的多尺度分析能力和OMP算法的稀疏信号重建能力，实现了高效、高质量的图像压缩。具体步骤如下：

对原始图像进行小波变换，得到一系列小波系数。
对小波系数进行稀疏表示，即将其表示为观测矩阵中少数列的线性组合。这一步可以通过OMP算法实现，将小波系数作为观测信号，选择合适的观测矩阵（如随机高斯矩阵）进行稀疏表示。
对稀疏表示后的系数进行量化编码，以进一步减少数据量。
在接收端，对量化编码后的系数进行解码，得到稀疏表示的系数。
利用OMP算法和观测矩阵重构小波系数。
对重构后的小波系数进行逆小波变换，得到压缩后的图像。

基于小波变换和OMP的图像压缩算法充分利用了小波变换的多尺度分析能力和OMP算法的稀疏信号重建能力，实现了高效、高质量的图像压缩。该算法在保留图像重要特征的同时，有效地去除了冗余信息，降低了存储和传输成本。在实际应用中，可以根据具体需求调整小波基函数、观测矩阵和稀疏度等参数，以达到最佳压缩效果。

4.matlab程序

function hat_y=omp(s,T,N)                          %定义omp函数，输入参数为测量值向量s，传感矩阵T和稀疏度N  
                                                   %获取传感矩阵T的大小，返回一个包含行数和列数的数组  
Size=size(T);                                     %  提取传感矩阵T的行数，即测量值的数目  
M=Size(1);                                        %  初始化待重构的谱域(变换域)向量为长度为N的零向量 
hat_y=zeros(1,N);                                                  
Aug_t=[];                                         %  初始化增量矩阵为空矩阵  
r_n=s;                                            % 初始化残差值为测量值向量s  

for times=1:M/4;                                  % 开始迭代，迭代次数设定为测量值数目的1/4（这里可能是一个经验值或者特定设置）  
    for col=1:N;                                  % 遍历传感矩阵T的所有列向量 
        product(col)=abs(T(:,col)'*r_n);          % 计算传感矩阵的每一列与当前残差的内积，并取其绝对值  
    end
    [val,pos]=max(product);                       %  找到内积绝对值最大的列，并返回其值和位置
    Aug_t=[Aug_t,T(:,pos)];                       %  将找到的列添加到增量矩阵中
    T(:,pos)=zeros(M,1);                          %  将传感矩阵中已选中的列置为零（实际上应该去掉这列，但这里简化了操作）
    aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s;           %  使用最小二乘法求解当前增量矩阵下的稀疏系数  
    r_n=s-Aug_t*aug_y;                            %  更新残差
    pos_array(times)=pos;                         %  记录本次迭代中找到的列的位置
    
    if (norm(r_n)<9)                              %   判断残差二范数是否小于9（这个阈值可能需要根据具体问题调整）  
        break;
    end
end
hat_y(pos_array)=aug_y;                           %  根据记录的位置信息，将稀疏系数赋值给重构向量对应的位置

 

function ww=DWT(N)

[h,g]= wfilters('sym8','d');       % 获取'sym8'小波的低通和高通分解滤波器系数  

% （注释掉的代码）指定输入信号的长度N，应为2的整数幂 
L=length(h);                       % 获取滤波器长度  
rank_max=log2(N);                  % 计算最大分解层数  
rank_min=double(int8(log2(L)))+1;  % 计算最小分解层数，但这里使用int8可能不是最佳选择，建议使用floor  
ww=1;  % 初始化变换矩阵为1（这里应该是初始化一个单位矩阵，但代码有误）  

%  矩阵构造
for jj=rank_min:rank_max% 从最小层数到最大层数进行循环 
    % 计算当前层的信号长度  
    nn=2^jj;
    
    %  构造向量
    p1_0=sparse([h,zeros(1,nn-L)]);% 构造稀疏格式的低通滤波器向量，后面补零  
    p2_0=sparse([g,zeros(1,nn-L)]);% 构造稀疏格式的高通滤波器向量，后面补零
    
    % 向量圆周移位  
    for ii=1:nn/2% 对每个位置进行循环移位以构造滤波器组  
        p1(ii,:)=circshift(p1_0',2*(ii-1))';% 低通滤波器向量循环移位
        p2(ii,:)=circshift(p2_0',2*(ii-1))';% 高通滤波器向量循环移位  
    end
    
    %  构造正交矩阵
    w1=[p1;p2];% 将移位后的低通和高通滤波器组合成正交矩阵的前半部分 
    mm=2^rank_max-length(w1);% 计算需要补零的行数（但这里的计算可能不正确）  
    w=sparse([w1,zeros(length(w1),mm);zeros(mm,length(w1)),eye(mm,mm)]);% 构造完整的正交变换矩阵，但这里逻辑可能有误
    ww=ww*w;% 累积变换矩阵（但初始ww应为单位矩阵）
    
    clear p1;clear p2;
end
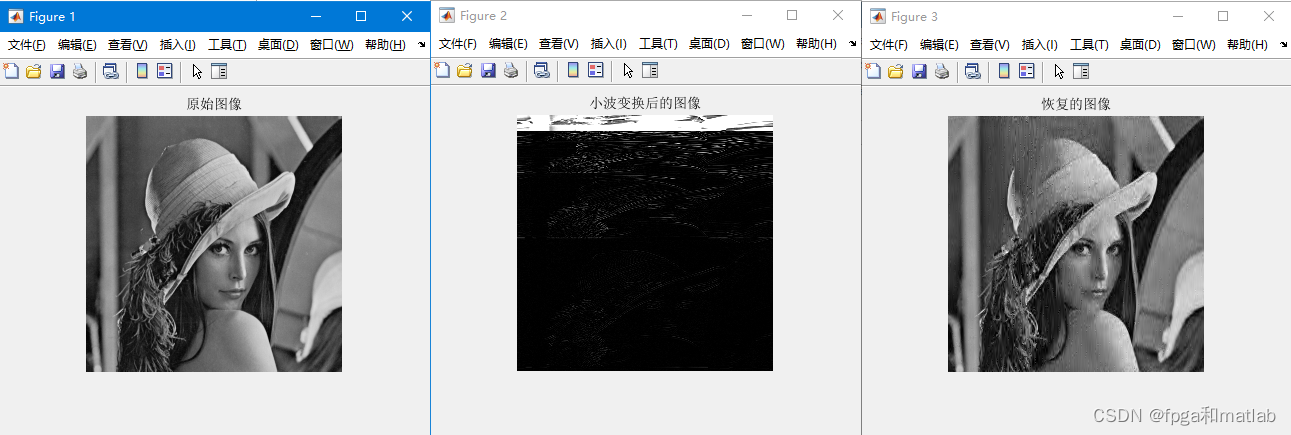
up4012

仿真结果如下：