目录
基于DCT变换和DCT逆变换的图像量化与反量化是数字图像处理中的重要技术,特别是在图像压缩领域,如JPEG标准中就广泛采用了这种技术。下面将详细介绍其原理。
1.DCT变换
离散余弦变换(DCT for Discrete Cosine Transform)是与傅里叶变换相关的一种变换,它类似于离散傅里叶变换(DFT for Discrete Fourier Transform),但是只使用实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的(因为一个实偶函数的傅里叶变换仍然是一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT有8种标准类型,其中4种是常见的)。DCT(离散余弦变换)是一种实数域的变换,其变换核是可分离的,且具有良好的能量集中性。在图像处理中,通常使用二维DCT变换。
一维DCT变换时二维DCT变换的基础,所以我们先来讨论下一维DCT变换。一维DCT变换共有8种形式,其中最常用的是第二种形式,由于其运算简单、适用范围广。我们在这里只讨论这种形式,其表达式如下:
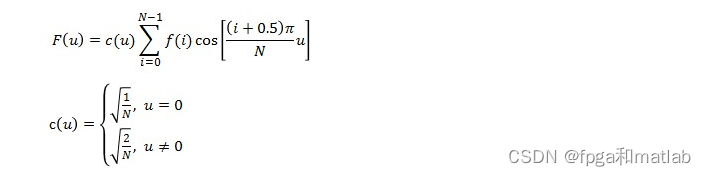
其中,f(i)为原始的信号,F(u)是DCT变换后的系数,N为原始信号的点数,c(u)可以认为是一个补偿系数,可以使DCT变换矩阵为正交矩阵。
二维DCT变换其实是在一维DCT变换的基础上在做了一次DCT变换,其公式如下:
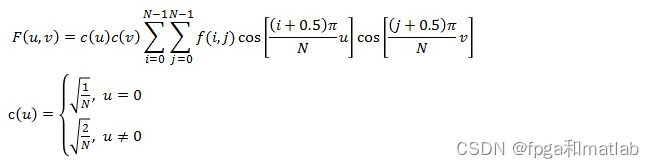
由公式我们可以看出,上面只讨论了二维图像数据为方阵的情况,在实际应用中,如果不是方阵的数据一般都是补齐之后再做变换的,重构之后可以去掉补齐的部分,得到原始的图像信息,这个尝试一下,应该比较容易理解。
2. DCT逆变换
在图像的接收端,根据DCT变化的可逆性,我们可以通过DCT反变换恢复出原始的图像信息,其公式如下:

在实际的图像处理中,DCT变换的复杂度其实是比较高的,所以通常的做法是,将图像进行分块,然后在每一块中对图像进行DCT变换和反变换,在合并分块,从而提升变换的效率。具体的分块过程中,随着子块的变大,算法复杂度急速上升,但是采用较大的分块会明显减少图像分块效应,所以,这里面需要做一个折中,在通常使用时,大都采用的是8*8的分块。
3. 图像量化
图像量化是将连续或大范围的数值映射到有限的离散值集合中的过程。在基于DCT的图像压缩中,量化的目的是减少DCT系数的精度,从而减少存储和传输所需的数据量。
图像经过DCT变换后,主要的低频能量都聚集于左上角,少量的高频能量于右下角。如下图所示。左上角为低频信号所在位置,右下角为高频信号所在位置。可以看到左上角颜色更亮,而右下角颜色更暗。亮色说明系数大,能量多,反之说明系数小,能量少。

这里量化的方式为保留左上角的低频信号,过滤右下角的高频信号。本文通过遮罩进行逐元素相乘来实现过滤。如下图所示。通过乘法,将遮罩中1的位置数据保留,0的部分删除。即可实现量化。或者可以通过系数的大小进行筛选,系数大于某个值就保留,否则删除。
4.反量化(解量化)
反量化(或解量化)是量化的逆过程,其目的是从量化的系数中恢复出原始的DCT系数(或近似值)。通过反量化,我们得到了近似的DCT系数。需要注意的是,由于量化过程中引入了误差,因此通常不等于原始的DCT系数(F(u, v))。
5.matlab程序与仿真
% 获取输入图像的行数(像素值)
rows = size(image,1);
% 获取输入图像的列数(像素值)
columns = size(image,2);
% 计算并显示图像的熵
image_entropy = entropy(image) ;
display([image_entropy]);
% 定义量化矩阵Q1
Q1 = [ [16 11 10 16 24 40 51 61];[12 12 14 19 26 58 60 55];
[14 13 16 24 40 57 69 56];[14 17 22 29 51 87 80 62];
[18 22 37 56 68 109 103 77];[24 35 55 64 81 104 113 92];
[49 64 78 87 103 121 120 101];[72 92 95 98 112 100 103 99]
] ;
% 初始化DCT块矩阵为零矩阵,大小与输入图像相同
dct_blocks = zeros(rows,columns);
% 对输入图像进行8x8分块的DCT变换
for i = 1:8:rows % 行循环,步长为8
for j = 1:8:columns % 列循环,步长为8
dct_blocks(i:(i+7),j:(j+7))= dct2(image(i:(i+7),j:(j+7)));
end
end
% 初始化量子化块矩阵为零矩阵,大小与输入图像相同
quantum_blocks = zeros(rows,columns);
% 对DCT块进行量子化操作
for i=1:8:rows
for j=1:8:columns
quantum_blocks(i:(i+7),j:(j+7)) = round(dct_blocks(i:(i+7),j:(j+7))./Q1);
end
end
% 取量子化块的绝对值,并转换为uint8类型
absolute_quantum_blocks = uint8(abs(quantum_blocks));
% 计算并显示量子化块的熵
quantum_entropy = entropy(absolute_quantum_blocks);
% 初始化反量子化块矩阵为零矩阵,大小与输入图像相同
reverse_quantum_blocks = zeros(rows,columns);
% 对量子化块进行反量子化操作(乘以Q1)
for i=1:8:rows
for j=1:8:columns
reverse_quantum_blocks(i:(i+7),j:(j+7)) = quantum_blocks(i:(i+7),j:(j+7)).* Q1;
end
end
% 初始化反DCT块矩阵为零矩阵,大小与输入图像相同
reverse_dct_blocks = zeros(rows,columns);
% 对反量子化块进行IDCT变换,得到近似图像块
for i=1:8:rows
for j=1:8:columns
reverse_dct_blocks(i:(i+7),j:(j+7)) = idct2(reverse_quantum_blocks(i:(i+7),j:(j+7)));
end
end
% 将反DCT块转换为uint8类型,得到新图像New_Image
New_Image = uint8(reverse_dct_blocks);
% 计算原始图像与新图像之间的均方误差(MSE)和峰值信噪比(PSNR)
Sums = sum(sum((double(image)-double(New_Image)).^2));% 计算差值的平方和
N = rows * columns ;% 图像的总像素数
MSE = Sums / N ;% 计算均方误差MSE
% 计算峰值信噪比PSNR (假设最大像素值为255)
PSNR = 10 * log10(255*255/MSE) ;
display([PSNR]);
figure;
imagesc(New_Image);
title('New Image : Q1');
colormap(gray);
up4011最后量化后的图像性能测试结果如下:
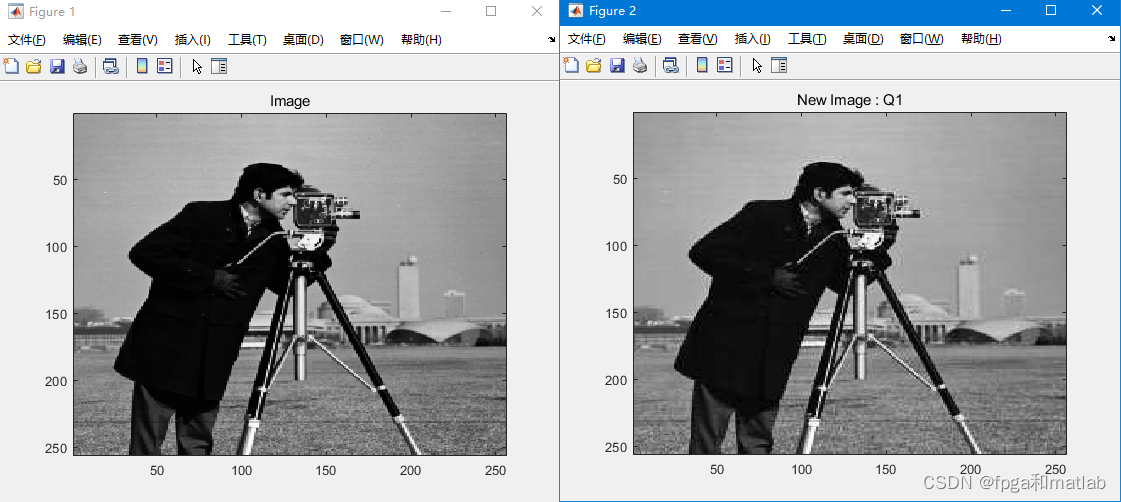
image_entropy =
7.0097
PSNR =31.7444
综上所述,基于DCT变换和DCT逆变换的图像量化与反量化是数字图像处理中的关键技术之一。通过选择合适的量化矩阵和高效的算法实现,可以在保证图像质量的前提下实现较高的压缩比。然而,量化过程不可避免地会引入误差和信息丢失,因此在设计系统时需要权衡压缩效率和图像质量之间的关系。此外,在实际应用中还需要考虑计算复杂度和实时性等方面的要求。