目录
一.方阵-对角矩阵-单位矩阵
方阵:n x n阶矩阵
例如:3 x 3矩阵
对角矩阵:除主对角线的以外的值全为0
例如:
单位矩阵:主对角线上的值全为1,其余值全为0
例如:
三者的关系:单位矩阵对角矩阵
方阵
二.矩阵与向量
行向量:1 x n的矩阵
例如:
列向量:n x 1的矩阵
例如:
三.矩阵的转置
定义:M矩阵的转置为M矩阵沿着主对角线反转,记作
公式:
定理:
若M为对角矩阵则:
三.矩阵乘法
1.标量与矩阵相乘
设M为矩阵,k为常数则:
2.矩阵与矩阵相乘
设M1:a行b列矩阵,M2:b行c列矩阵
条件:第一个矩阵的列等于第二个矩阵的行
结果:M1 * M2为a行c列矩阵
公式:
例如:
3.矩阵乘法的特点
1.矩阵乘以对应的单位矩阵等于他本身
2.不满足交换律
AB BA
3.满足结合律
(AB)C = A(BC)
4.
四.向量矩阵转换
1.向量矩阵相乘
用途:可用于向量的转换,在DX中使用的是行向量,openGL中使用的是列向量
设
设
总结:行向量左乘乘矩阵,列向量右乘矩阵
2.矩阵转换向量
设
将向量转换成矩阵并分解:
化简:
我们令
于是得到:
其中p,q,r又被称之为基向量
五.二维旋转矩阵
令,则
被称为二维旋转矩阵
用途:计算绕原点旋转
后得到的向量
公式:
证明:
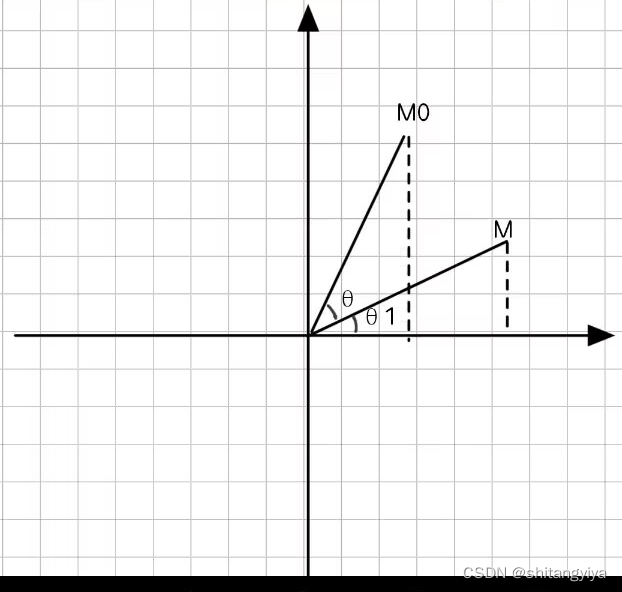
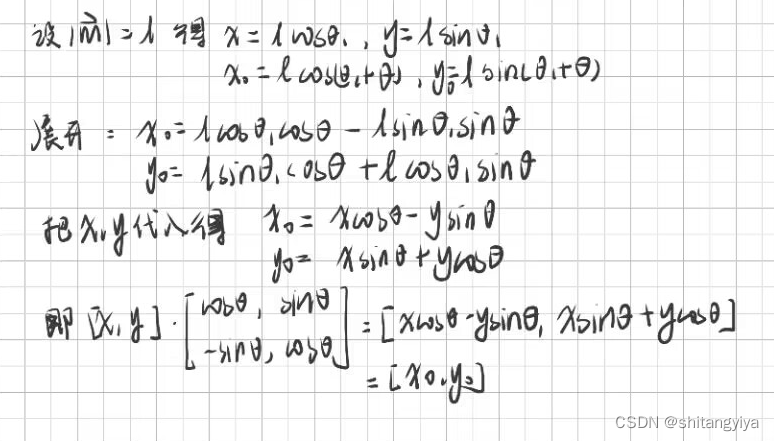
六.三维绕轴旋转
左手坐标系:
右手坐标系: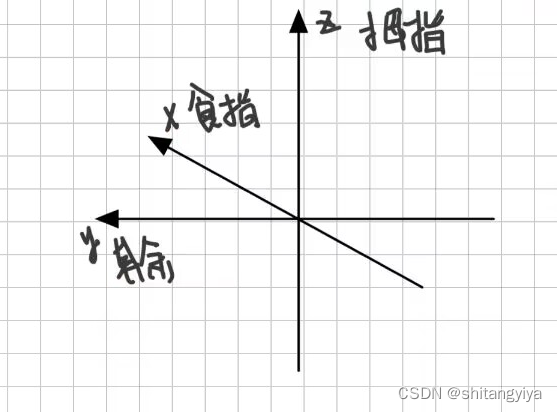
角旋转正方向的判断,左手定则:大拇指指向需要旋转的轴,从轴的正端点,指向负端点旋转(左手坐标系为顺时针,右手坐标系为逆时针)
绕z轴旋转
绕x轴旋转
绕y轴旋转
七.绕任意轴旋转
如图为绕
旋转
得到
,其中OH垂直面AMH
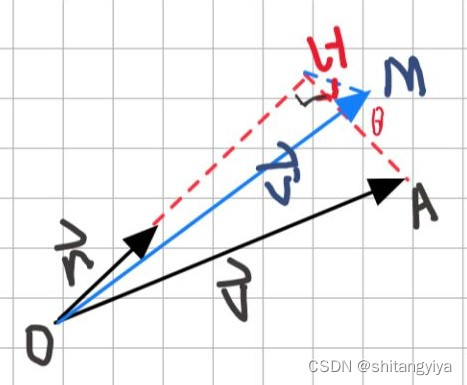
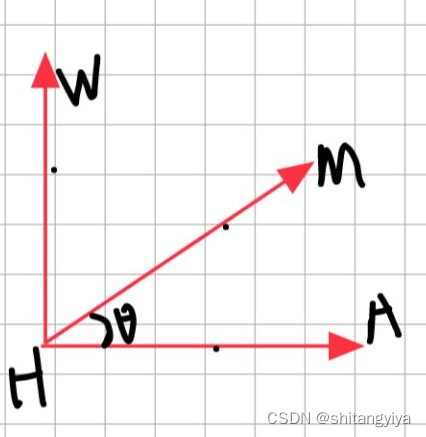
我们将面AMH单独拿出来看,做HW垂直于HA,令HW等于HA
我们可以得到: ..........................
..........................2
解释:怎么得到的
在
方向上的投影为
,
的单位向量为
,我们假设n为单位向量长度为1
..........................3
由1,2,3得:
化简得:
我们设
我们求各个方向上的向量
九.沿轴缩放矩阵
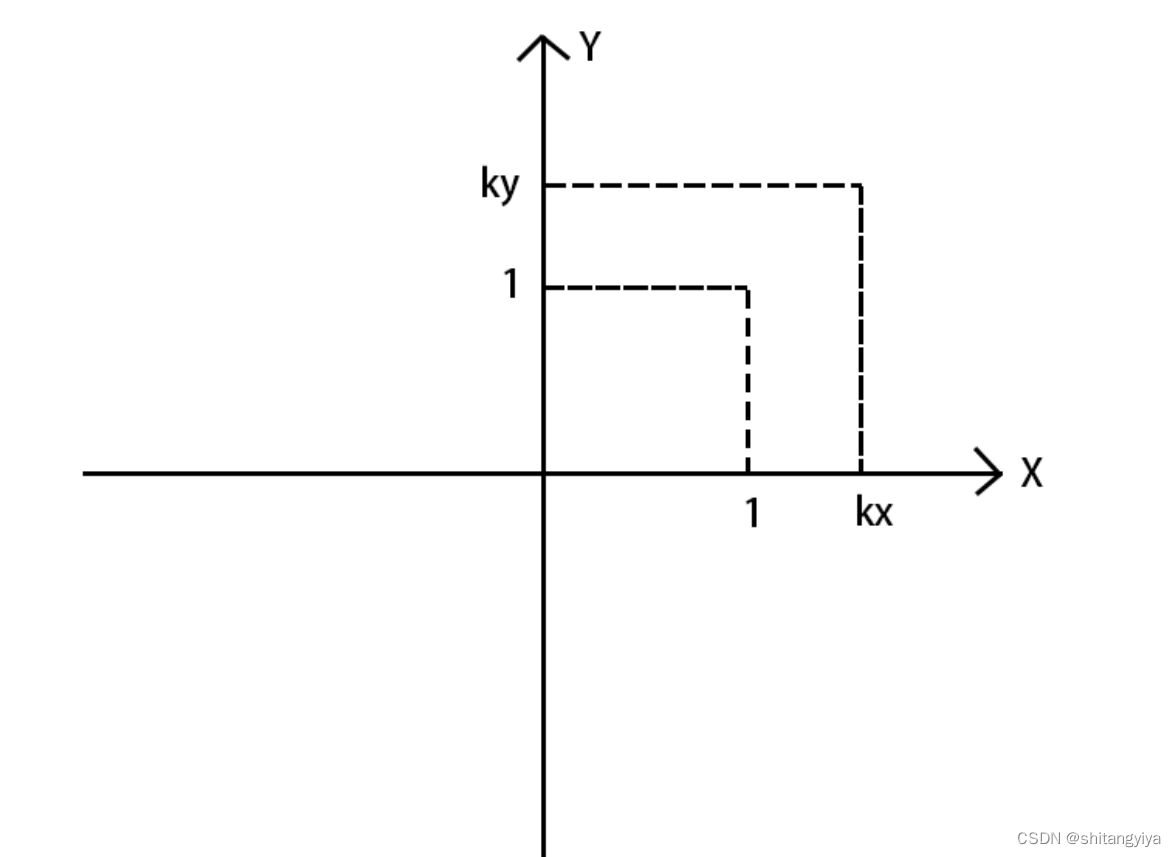
设基向量
二维缩放矩阵
同理,三维缩放矩阵
十.沿任意轴缩放矩阵
1.二维缩放矩阵
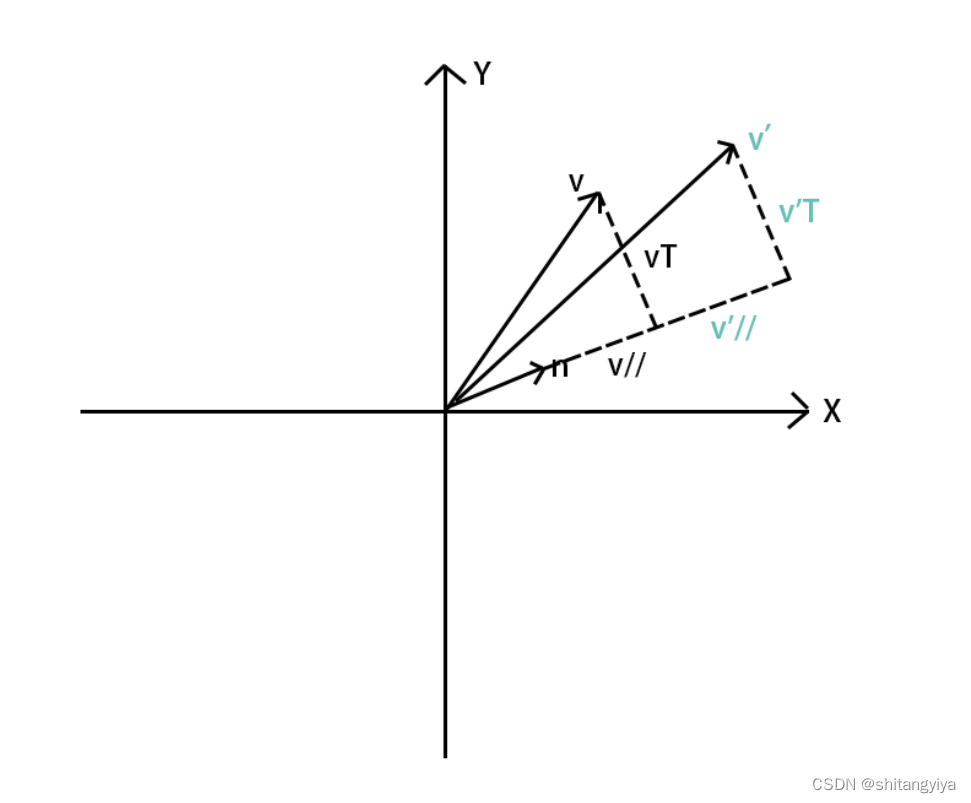
设沿
方向缩放k倍得到
设基向量计算变换后的向量
把带入得:
所以二维缩放矩阵为:
2.三维缩放矩阵
证明过程同二维,在这里直接给出结果
三维缩放矩阵为
十一.正交投影
设于投影垂直,
为正交投影,其中0称为缩放因子,缩放因子为0时代表投影,-1代表镜像
1.二维
向x轴投影,向y轴投影
例如向量(1,1)向x轴投影:
2.三维
向xoy面投影
向xoz面投影
向yoz面投影
十二.沿任意轴的正交投影
1.二维
2.三维
十三.镜像投影
1.二维
2.三维
十四.切变
1.二维
s,为切变因子
2.三维