概述：在对支持向量机的学习和使用过程中，遇到了许许多多的问题，通过查阅各种资料，也是逐一攻克了遇到的问题。感悟颇多，写此博文的目的是想以一个学习者的身份从一个刚接触支持向量机的角度去记录模型推到过程中的种种困惑以及理解过程，以帮助更多人的更省时的了解和学习支持向量机；
本文主要记录和解决的问题：
说明：每个问题所标的星级表示此问题的理解对后边推导过程的影响程度，也就是说理解不到位会使得自己越看越糊涂（仅供参考）
1.我自己学习和推到支持向量机的过程路线
2.三维空间中点到直线的距离的计算，以及分离超平面的方程（5颗星）
3.Lagrange乘子法的原理（5颗星）
4.凸优化的基本概念以及原理（5颗星）
5.对偶算法原理（5颗星）
6.向量求导（5颗星）
下边就上述的每一个问题进行整理
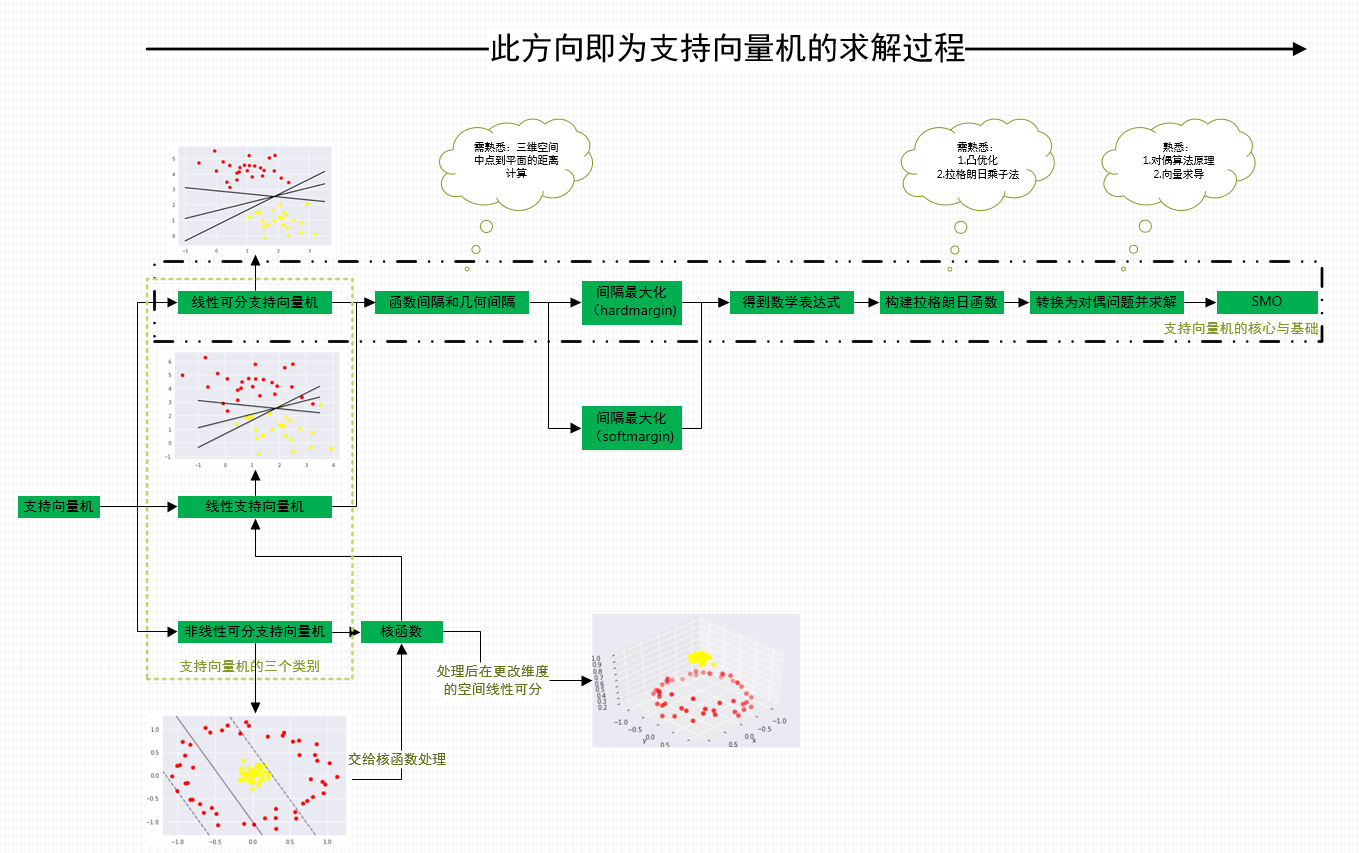
问题1：下图是我对支持向量机的整个知识体系所涉及到的相应的知识的一个整理，图中同时也描述了各支持向量机之间的关系。
问题2:“三维空间中点到直线的距离的计算”
(1).点到平面的距离
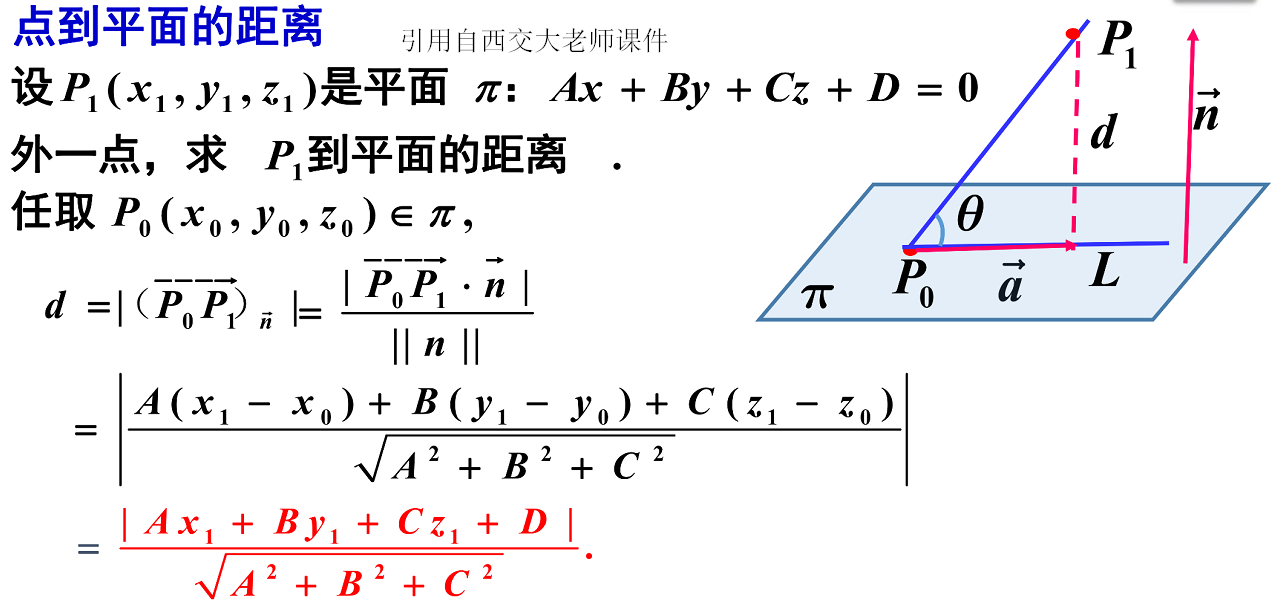
(2).分离超平面方程
问题3：Lagrange乘子法原理
Lagrange乘子法的作用主要是用来解决条件极值问题的一种方法；
条件极值的概念：对自变量除定义域限制外，还有其他条件限制。举例：例如求f(x,y)在条件g(x,y)= 0下的条件极值，称f(x,y)为目标函数，方程g(x,y)=0为约束条件，变量x,y为决策变量；
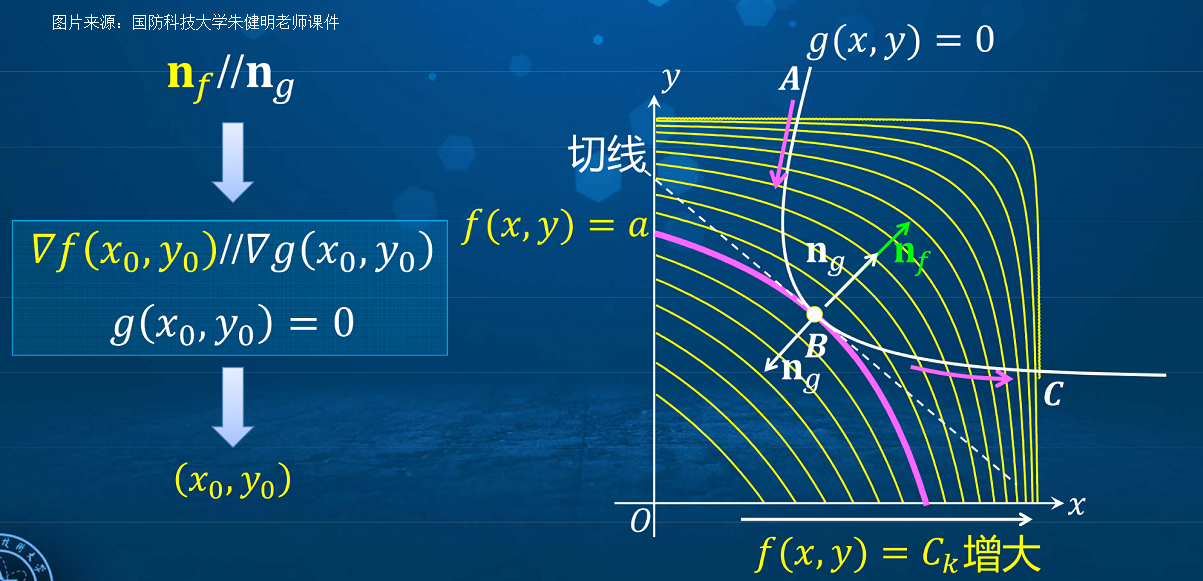
如下图所示，假设g(x,y)=0的图像如下图所示，f（x,y）的等高线沿着x方向增大，有图示做直观分析，由A点到B点f(x,y)的值逐渐减小，由B点到C点f(x,y)的值逐渐增大。很显然在B点时f(x,y)取得了最小值，分析一下B点处g(x,y)=0所表示的曲线和f(x,y)等高线的关系。在B点处g(x,y)=0所表示的曲线和f(x,y)在B处的等高线必然是相切的。为了理解这样相切的关系，我们可以假设一只蚂蚁正在验证g(x,y)=0所表示的曲线的A处爬向C处，假如在B点f(x,y)的等高线穿过了B点，则到B点时蚂蚁还未爬到白色曲线的最底端，也就说明继续往底部爬最能找到别的等高线与曲线最低点相切。既然相切，那说明在B出等高线和g(x,y)所表示的曲线有公共切线，所以如下图f(x,y)在B点(假设B点的左边为(x0,y0))的法向量nf 和g(x,y)=0在B处的法向量共线（方向可能相同也可能不同），而曲线在B点处的梯度向量即为法向量，由此就可知他们的梯度向量共线。由此便可得到如下方程：
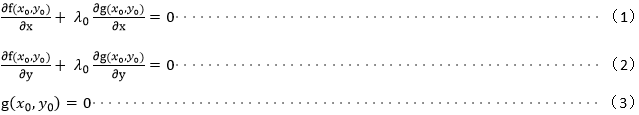
构造函数：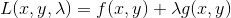
其在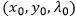
取得极值的条件为
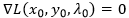，和上述(1)(2)(3)完全等价
\[L(x,y,\lambda ) = f(x,y) + \lambda g(x,y)\]
我们构造一个函数，此函数成为拉格朗日函数，其在取得极值的条件为和上市等价
