机器学习实战(用Scikit-learn和TensorFlow进行机器学习)(九)

上几节介绍了多种模型（线性模型、支持向量机、集成学习），这一节介绍一类新的预处理方法。 


九、降维（Dimensionality Reduction）

  在现实生活中很多机器学习问题有上千维，甚至上万维特征，这不仅影响了训练速度，通常还很难找到比较好的解。这样的问题成为维数灾难（curse of dimensionality）

  幸运的是，理论上降低维度是可行的。比如MNIST数据集大部分的像素总是白的，因此可以去掉这些特征；相邻的像素之间是高度相关的，如果变为一个像素，相差也并不大。

  需要注意：降低维度肯定会损失一些信息，这可能会让表现稍微变差。因此应该先在原维度训练一次，如果训练速度太慢再选择降维。虽然有时候降为能去除噪声和一些不必要的细节，但通常不会，主要是能加快训练速度。

  降维除了能训练速度以外，还能用于数据可视化。把高维数据降到2维或3维，然后就能把特征在2维空间（3维空间）表示出来，能直观地发现一些规则。

  本节会将两种主要的降维方法(projection and Manifold Learning)，并且通过3中流行的降维技术：PCA，Kernel PCA和LLE。 


1、维数灾难

  在高维空间中，许多表现和我们在低维认识的差别很大。例如，在单位正方形（1×1）内随机选点，那么随机选的点离所有边界大于0.001（靠近中间位置）的概率为0.4%（1 - 0.99821 - 0.9982），但在一个10000维单位超立方体（1×1×⋯×1），这个概率大于99 999999%（1 - 0.998100001 - 0.99810000）。因此高维超立方体中的大多数随机点都非常接近边界。

  在高维空间中还有一个与认识不同的：如果在单位超立方体（1×1×⋯×1）随机选两个点，在2维空间，两个点之间平均距离约为0.52；在3维空间约为0.66，在1,000,000维空间，则约为408.25，可以看到在单位立方体中两个点距离竟然能相差这么大。因此在高维空间，这很可能会使得训练集和测试集相差很大，导致训练过拟合。

  理论上，只要通过增加训练集，就能达到训练空间足够密集。但是随着维度的增加，需要的训练集是呈指数增长的。如果100维（比MNIST数据集还要小），要达到每个样本的距离为0.1（平均的分散开）的密度，则需要的样本为1010010100个样本，可见需要的样本之多。 


2、降维的主要方法

  降为的方法主要为两种：projection 和 Manifold Learning。

投影（Projection）

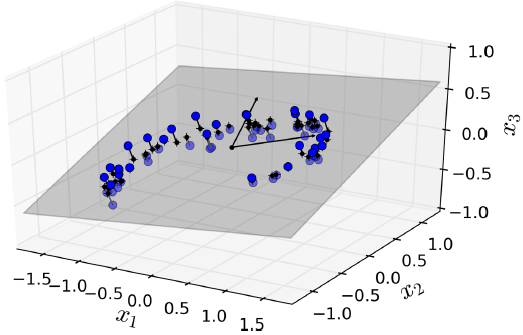
  在大多数的真实问题，训练样例都不是均匀分散在所有的维度，许多特征都是固定的，同时还有一些特征是强相关的。因此所有的训练样例实际上可以投影在高维空间中的低维子空间中，下面看一个例子。

          

  可以看到3维空间中的训练样例其实都分布在同一个2维平面，因此我们能够将所有样例都投影在2维平面。对于更高维的空间可能能投影到低维的子空间中。

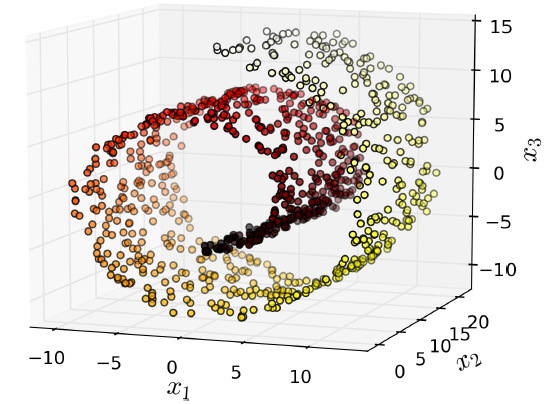
  然而投影（projection）不总是降维最好的方法在，比如许多情况下，空间可以扭转，如著名的瑞士卷（Swiss roll）数据。

         

  如果简单的使用投影（project）降维（例如通过压平第3维），那么会变成如下左图的样子，不同类别的样例都混在了一起，而我们的预想是变成右下图的形式。

       


流行学习（Manifold Learning）

  瑞士卷（Swiss roll）是二维流形的例子。它可以在高维空间中弯曲。更一般地，一个d维流形在n维空间弯曲（其中d＜n）。在瑞士卷的情况下，D＝2和n＝3。

  基于流行数据进行建模的降维算法称为流形学习（Manifold Learning）。它假设大多数现实世界的高维数据集接近于一个低维流形。

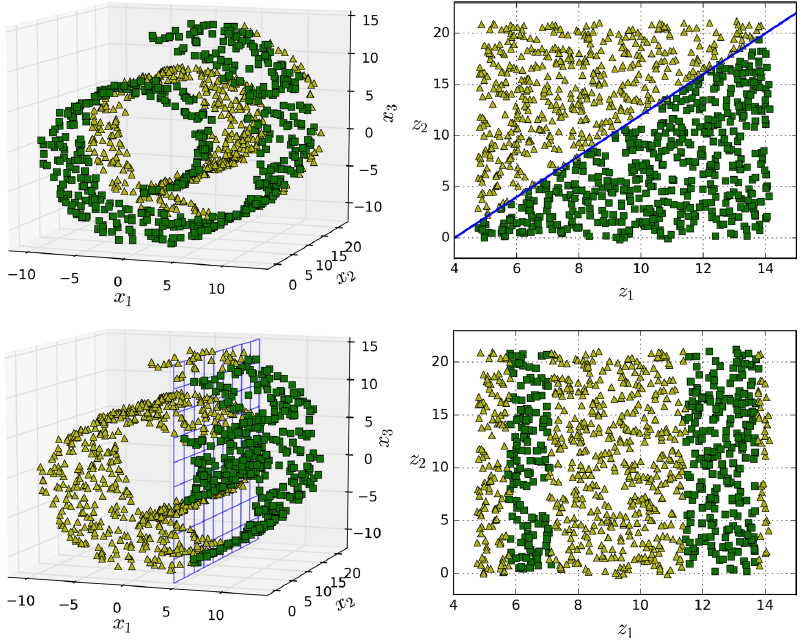
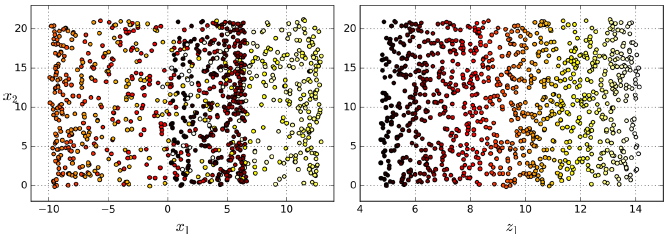
  流行假设通常隐含着另一个假设：通过流形在低维空间中表达，任务（例如分类或回归）应该变得简单。如下图第一行，Swiss roll分为两类，在3D的空间看起来很复杂，但通过流行假设到2D就能变得简单。

  但是这个假设并不总是能成立，比如下图第二行，决策线为x=5，2D的的决策线明显比3D的要复杂。因此在训练模型之前先降维能够加快训练速度，但是效果可能会又增有减，这取决于数据的形式。

    

  下面介绍几种著名的降维技术。 


3、主成分分析（PCA）

  主成分分析（PCA）是用的最出名的降维技术，它通过确定最接近数据的超平面，然后将数据投射(project)到该超平面上。 


保留最大方差

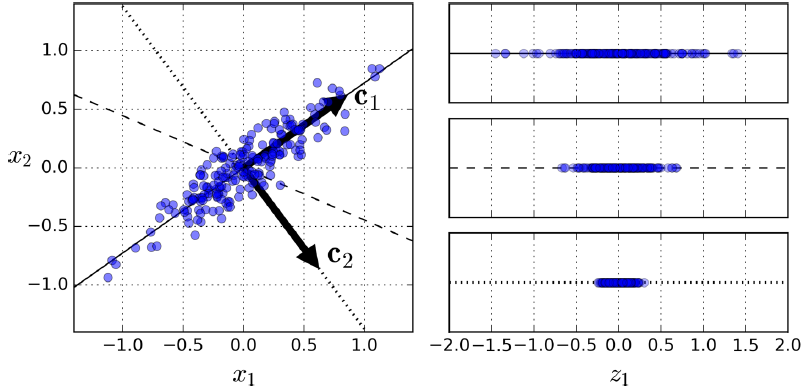
  首先需要选择一个好的超平面。先看下图的例子，需要将2D降为1D，选择不同的平面得到右图不一样的结果，第1个投影以后方差最大，第3个方差最小，选择最大方差的一个感觉上应该是比较合理的，因为这样能保留更多的信息。

      

  另外一种判断的方式是：通过最小化原数据和投影后的数据之间的均方误差。 


主成分（Principal Components）

  算法首先找到第一个主成分，使得投影后方差最大，如上图的c1。然后再找第二个主成分（要和第一个主成分正交）使得上面投影后的数据集再投影后方差最大，由于上图是2D平面，因此只有c2符合。如果是n维平面，则找第(t<=n）个主成分（要和1,2,…,t-1个主成分都正交），使得t-1投影后的数据再投影后方差最大。

  需要注意：主成分的方向是不稳定的，如果稍微扰动数据，则可能使方向相反，不过仍会在同一个轴上。在某些情况下，一对主成分甚至可以旋转或交换，但它们定义的平面一般保持不变。

  要如何才能在训练集中找到这些主成分？我们可以通过奇异值分解（SVD）来把X矩阵分解为三个矩阵U*∑*VTU*∑*VT，其中VTVT矩阵的每一个列向量就是我们要找的主成分。

  Numpy中提供svd()方法，下面为求主成分的例子

#产生数据
import numpy as np
x1=np.random.normal(0,1,100)
x2=x1*1+np.random.rand(100)
X=np.c_[x1,x2]
#svd分解求出主成分
X_centered = X - X.mean(axis=0)
U, s, V = np.linalg.svd(X_centered)
c1 = V.T[:, 0]
c2 = V.T[:, 1]

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

  需要注意：PCA假设数据以原点为中心，因此要先减去均值再svd分解。Scikit-learn中的PCA类已经减去均值，但是如果在别的场景使用要记得先减去均值再求主成分。 


投影到d维空间

  得到主成分以后就能将数据降维，假设降到d维空间，则用数据矩阵与前d个主成分形成的矩阵相乘，得到降维后的矩阵。

Xd=X∗WdXd=X∗Wd

  对应的代码为：

d=1
Wd = V.T[:, :d]
XD = X_centered.dot(Wd)

• 1
• 2
• 3

使用Scikit-Learn

  Scikit-learn提供了PCA类，n_components控制维数

from sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XD = pca.fit_transform(X)

• 1
• 2
• 3

  fit以后可以通过components_变量来输出主成分，还可以通过explained_variance_ratio_来查看每个主成分占方差的比率。

#查看主成分
pca.components_.T
#显示PCA主成分比率
print("主成分方差比率为：")
print(pca.explained_variance_ratio_)

• 1
• 2
• 3
• 4
• 5

  

  在这个2D空间，可以看到第一个主成分占训练集方差的97%，即第二个主成分占训练集方差的3%，因此假设第二个主成分含有的信息比较少时比较合理的。 


选择合理的维数

  合理的选择维数而不是随机选择一个维数，我们可以通过设置一个合适的方差比率（如95%），计算需要多少个主成分的方差比率和能达到这个比率，就选择该维度，对应代码如下。（除非需要将数据降到2D或3D用于可视化等）

pca = PCA()
pca.fit(X)
cumsum = np.cumsum(pca.explained_variance_ratio_) #累加
d = np.argmax(cumsum >= 0.95) + 1

• 1
• 2
• 3
• 4

  得到维度d后再次设置n_components进行PCA降维。当然还有更加简便的方法，直接设置n_components_=0.95，那么Scikit-learn能直接作上述的操作。

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X)

• 1
• 2

增量PCA（IPCA）

  当数据量较大时，使用SVD分解会耗费很大的内存以及运算速度较慢。幸运的是，可以使用IPCA算法来解决。先将训练样本分为mini-batches，每次给IPCA算法一个mini-batch，这样就能处理大量的数据，也能实现在线学习（当有新的数据加入时）。

  下面是使用Numpy的array_split()方法将MNIST数据集分为100份，再分别喂给IPCA，将数据降到154维。需要注意，这里对于mini-batch使用partial_fit()方法，而不是对于整个数据集的fit()方法。

#加载数据
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
X = mnist["data"]
#使用np.array_split（）方法的IPCA
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X, n_batches):
    inc_pca.partial_fit(X_batch)
X_mnist_reduced = inc_pca.transform(X)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

  还可以使用Numpy 的memmap类来操纵储存在硬盘上的二进制编码的大型数据，只有当数据被用到的时候才会将数据放入内存。由于IPCA每次只需将一部分数据，因此能通过memmap来控制内存。由于使用的是输入的是整个数据集，因此使用的是fit（）方法。

X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)

• 1
• 2
• 3
• 4

随机PCA

  随机PCA是个随机算法，能快速找到接近前d个主成分，它的计算复杂度为O(m∗d3)+O(d3)O(m∗d3)+O(d3)，而不是O(m∗n3)+O(n3)O(m∗n3)+O(n3)，如果d<

rnd_pca = PCA(n_components=154, svd_solver="randomized")
X_reduced = rnd_pca.fit_transform(X_mnist)

• 1
• 2

4、核PCA(Kernel PCA)

  在第六节的SVM中提到了核技巧，即通过数学方法达到增加特征类似的功能来实现非线性分类。类似的技巧还能用在PCA上，使得可以实现复杂的非线性投影降维，称为kPCA。该算法善于保持聚类后的集群(clusters)后投影，有时展开数据接近于扭曲的流形。下面是使用RBF核的例子。

#生成Swiss roll数据
from sklearn.datasets import make_swiss_roll
data=make_swiss_roll(n_samples=1000, noise=0.0, random_state=None)
X=data[0]
y=data[1]
#画3维图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
ax = plt.subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], X[:,2],c=y)
plt.show()
#kPCA
from sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

  需要注意，此方法要使用大量内存，可能会使内存溢出。

选择合适的核与参数

  由于kPCA是非监督算法，因此无法判断性能的好坏，因此需要结合分类或回归问题来判断。通过GridSearch来选择合适的核与参数，下面是一个例子：

from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
X,y = mnist["data"],mnist["target"]

from sklearn.decomposition import KernelPCA
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression())
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

5、LLE

  局部线性嵌入（Locally Linear Embedding）是另一种非线性降维技术。它基于流行学习而不是投影。LLE首先测量每个训练样例到其最近的邻居（CN）的线性关系，然后寻找一个低维表示使得这种相关性保持得最好（具体细节后面会说）。这使得它特别擅长展开扭曲的流形，特别是没有太多的噪音的情况。

  下面是使用Scikit-learn中的LocallyLinearEmbedding类来对Swiss roll数据降维。

#生成Swiss roll数据
from sklearn.datasets import make_swiss_roll
data=make_swiss_roll(n_samples=1000, noise=0.0, random_state=None)
X=data[0]
y=data[1]
#画3维图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
ax = plt.subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], X[:,2],c=y)
plt.show()
#LLe降维
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
#画出降为图
X_reduced = lle.fit_transform(X)
plt.scatter(X_reduced[:,0],X_reduced[:,1],c=y)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17

     

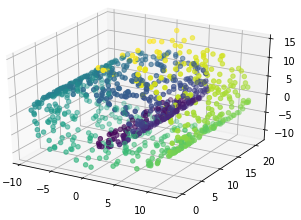
  可以看到，Swiss roll展开后局部保持的距离比较好。然而，但是对大的整体距离并不是保持的很好（右下角部分被挤压，左上角伸展）。但是LLE算法还是在流形中表现的很好。 


LLE原理

第一步：对于每一个训练样本x(i)x(i)，寻找离它最近的k个样本（如k=10），然后尝试重建x(i)x(i)与这些邻居的线性关系，即用这些邻居来线性表示x(i)x(i)。如下公式，最小化x(i)x(i)与这个线性表示的距离。其中非邻居的wi,jwi,j=0。

W^=argminW∑i=1m||x(i)−∑j=1mwi,jx(j)||2W^=arg⁡minW⁡∑i=1m||x(i)−∑j=1mwi,jx(j)||2

wi,j=0    if    i,j  is  not  neighborwi,j=0    if    i,j  is  not  neighbor

∑j=1mwi,jx(j)=1∑j=1mwi,jx(j)=1

第二步：将训练集降为d维(d < n)，由于上一步已经求出局部特征矩阵W^W^，因此在d维空间也要尽可能符合这个矩阵W^W^，假设样本x(i)x(i)降维变为z(i)z(i)，如下公式： 

Z^=argminZ∑i=1m||z(i)−∑j=1mw^i,jz(j)||2Z^=arg⁡minZ⁡∑i=1m||z(i)−∑j=1mw^i,jz(j)||2

  计算k个邻居的计算复杂度为：O(mlog(m)nlog(k))O(mlog⁡(m)nlog⁡(k))；优化权值的复杂度为：O(mnk3)O(mnk3)；重建低维向量的复杂度为：O(dm2)O(dm2)。如果训练样本数量过大，那么在最后一步重建m2m2会很慢。 


6、其它降维技术

  还有非常多降维的技术，有一些Scikit-learn也提供支持。下面简单列举一些比较有名的算法。

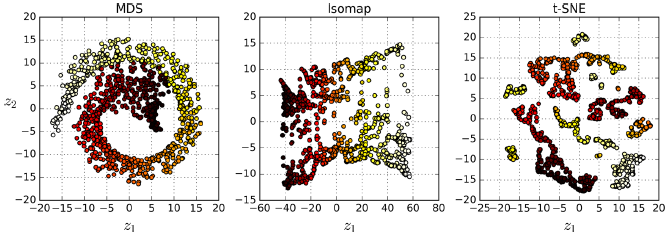
1、Multidimensional Scaling (MDS)降维的同时保留样本之间的距离，如下图。

2、Isomap通过连接每个样本和它的最近邻居来创建一个图，然后降低维的同时尝试保留样本间的测地距离(两个样本之间最少经过几个点)。

3、t-Distributed Stochastic Neighbor Embedding (t-SNE)，减少维度的同时试图保持相似的样本靠近和不同的样本分离。它主要用于可视化，特别是可视化高维空间中的聚类。

4、Linear Discriminant Analysis (LDA)，是一种分类算法，但是在训练定义了一个超平面来投影数据。投影使得同一类的样本靠近，不同一类的样本分开，所以在运行另一分类算法（如SVM分类器）之前，LDA是一种很好的减少维数的技术。