A Generalized Loss Function for Crowd Counting and Localization阅读笔记

简单来说，就是用了UOT来解决人群计数问题

代码：https://github.com/jia-wan/GeneralizedLoss-Counting-Pytorch.git
我改了一点的：https://github.com/Nightmare4214/GeneralizedLoss-Counting-Pytorch.git

loss

设density map为 A = { ( a i , x i ) } i = 1 n \mathcal{A} =\left\{\left(a_i, \mathbf{x}_i\right)\right\}_{i=1}^{n} A={ (ai​,xi​)}i=1n​
其中$a_i$为预测density，${\mathbf{x}}_i\in {\mathbb{R}}^n$为坐标，$n$为像素个数
令$\mathbf{a}={\left[a_i\right]}_i$，也就是density map转成列向量

真实点图为 B = { ( b j , y j ) } j = 1 m \mathcal{B}=\left\{\left(b_j,\mathbb{y}_j\right)\right\}_{j=1}^m B={ (bj​,yj​)}j=1m​
其中${\mathbf{y}}_j$为坐标，$m$为标注点个数，$b_j$为这个点代表的人群数量
这个论文假设$\mathbf{b}={\left[b_j\right]}_j=1_m$,也就是说每个点只有一个人

熵正则化的UOT为
$${\mathcal{L}}_{\mathbf{C}}^{\tau }\left(\mathcal{A},\mathcal{B}\right)=\underset{\mathbf{P}\in {\mathbb{R}}_{+}^{n\times m}}{\min }⟨\mathbf{C},\mathbf{P}⟩-ϵH\left(\mathbf{P}\right)+\tau D_1\left(\mathbf{P}{1}_m|\mathbf{a}\right)+\tau D_2\left({\mathbf{P}}^T{1}_n|\mathbf{b}\right)$$
其中$\mathbf{C}\in {\mathbb{R}}_{+}^{n\times m}$是传输代价矩阵,$C_{i,j}$为将density从${\mathbf{x}}_i$搬运到${\mathbf{y}}_j$的距离
$\mathbf{P}$为传输矩阵
令$\hat{\mathbf{a}}=\mathbf{P}{1}_m,\hat{\mathbf{b}}={\mathbf{P}}^T{1}_n$

这个loss有4个部分
第一部分是传输的loss，目的是将预测的density map往真实标注靠
第二部分是熵$H\left(\mathbf{P}\right)=-{\sum }_{i,j}{P}_{i,j}\log P_{i,j}$是熵正则化项，用来控制稀疏程度，越大越稀疏（会趋于均匀分布），反之亦然

第三部分就是希望$\hat{\mathbf{a}}$靠近$\mathbf{a}$
第四部分就是希望$\hat{\mathbf{b}}$靠近$\mathbf{b}$

论文里，$D_1$取$L_2$的平方
$D_2$取$L_1$

代价矩阵

$$C_{i,j}=e^{\frac{1}{\eta \left(x_i,y_j\right)}\Vert {\mathbf{x}}_i-{\mathbf{y}}_j{\Vert }_2}$$
这里的${\mathbf{x}}_i,{\mathbf{y}}_j$是经过归一化的
不过要注意，代码里这个$\eta \left(x_i,y_j\right)$是常数，默认是$0.6$

求解

采用的是sinkhorn
$$\mathbf{P}=\mathrm{diag}(\mathbf{u})\mathbf{K}\mathrm{diag}(\mathbf{v}),\mathbf{K}=\exp (-\mathbf{C}/\epsilon )$$
这里近似$D_1,D_2$为KL散度，这样的话有高效的解法
$${\mathbf{u}}^{(\ell +1)}={\left(\frac{\mathbf{a}}{\mathbf{K}{\mathbf{v}}^{(\ell )}}\right)}^{\frac{\tau }{\tau +ϵ}},{\mathbf{v}}^{(\ell +1)}={\left(\frac{\mathbf{b}}{{\mathbf{K}}^{\top }{\mathbf{u}}^{(\ell +1)}}\right)}^{\frac{\tau }{\tau +ϵ}}$$

(其实即使是$KL$散度，他代码似乎也不能这么写)

代码

数据集

预处理

用的是UCF-QNRF

预处理：
1.让$h,w$中较小的那个，处于$\left[512,2048\right]$的范围，另一个按照缩放比例调整
2.过滤不在图片中的点
3.额外计算每个点到其他点的一个距离，具体地
$$\mathbf{P}=\left(\begin{array}{c}{\mathbf{p}}_1^T\\ {\mathbf{p}}_2^T\\ ⋮\\ {\mathbf{p}}_m^T\end{array}\right),{\mathbf{p}}_i\in {\mathbb{R}}^2$$
$$\mathbf{dis}={\left[\Vert {\mathbf{p}}_i-{\mathbf{p}}_j\Vert \right]}_{i,j}$$

最后对每一行进行快排的那个选择哨兵的过程，找到第3个（从0开始数）
对第$1,2,3$个元素取平均（从0开始数）

def find_dis(point):
    a = point[:, None, :]
    b = point[None, ...]
    dis = np.linalg.norm(a - b, ord=2, axis=-1)  # dis_{i,j} = ||p_i - p_j||
    # mean(4th_min, 2 of the [1st_min, 2nd_min, 3rd_min])
    dis = np.mean(np.partition(dis, 3, axis=1)[:, 1:4], axis=1, keepdims=True)
    
    return dis

因此得到的标签为
$$\mathbf{P}={\left[\left(x_i,y_i,di{s}_i\right)\right]}_i\in {\mathbb{R}}^{m\times 3}$$

读取数据

随机裁剪图片，到$\left(512,512\right)$
设$i,j$为裁剪的左上角坐标，$h=w=512$

接着读取标签
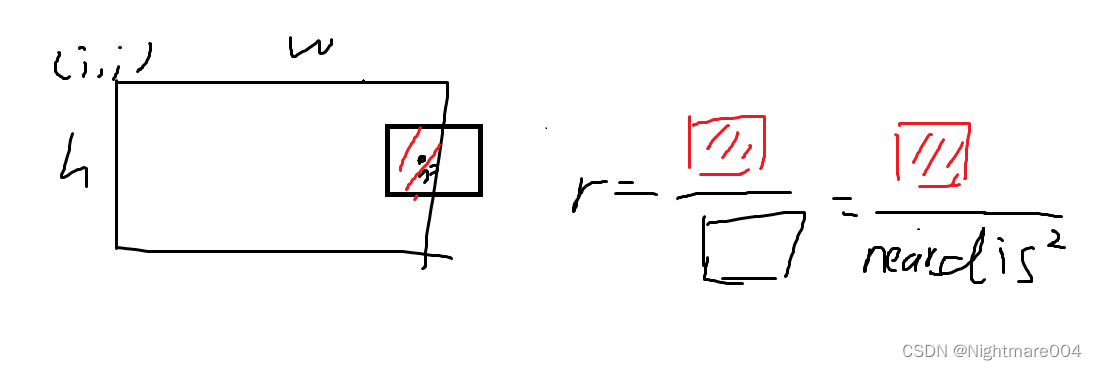
根据$dis$来设定一个小矩形
计算这个矩形在裁剪范围的面积，和矩形面积的$\frac{1}{4}$
如果这个比例大于0.3，就选择这个点，否则舍弃

然后其他的就是随机水平翻转

模型

vgg19+上采样+两层卷积+abs

训练

注意这里sinkhorn是有$ϵ-\text{scaling heuristic}$的这样可以做到20轮以内收敛
为了数值稳定，还用了$\text{log-domain}$

结果

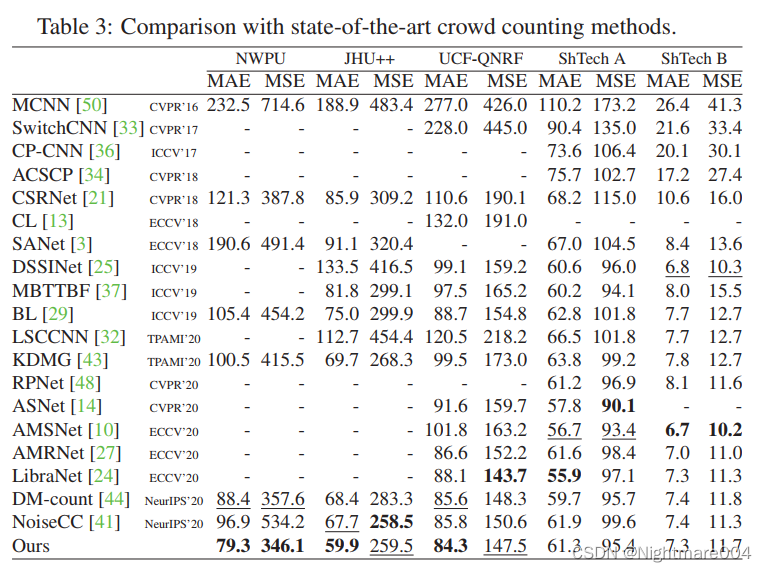
作者的提供的模型的结果：mae 85.09911092883813, mse 150.88815648865386
我在UCF-QNRF跑的结果：mae:85.69232401590861, mse:155.30853159819492