Distribution Matching for Crowd Counting阅读笔记

用OT来解决人群计数问题

用了OT+count loss + TV loss
证明OT的泛化误差比density map和Bayesian Loss

OT

考虑两个分布$\mathcal{X}={\left\{{\mathbf{x}}_i\mid {\mathbf{x}}_i\in {\mathbb{R}}^d\right\}}_{i=1}^n$，$\mathcal{Y}={\left\{{\mathbf{y}}_j\mid {\mathbf{y}}_j\in {\mathbb{R}}^d\right\}}_{j=1}^n$
考虑两个测度$\mathbf{\mu },\mathbf{\nu }$, $1_n^T\mathbf{\mu }=1_n^T\mathbf{\nu }=1$

设代价$c:\mathcal{X}\times \mathcal{Y}\mapsto {\mathbb{R}}_{+}$
代价矩阵${\mathbf{C}}_{ij}=c\left({\mathbf{x}}_i,{\mathbf{y}}_j\right)$
传输矩阵：$\Gamma =\left\{\mathbf{\gamma }\in {\mathbb{R}}_{+}^{n\times n}:\mathbf{\gamma }1=\mathbf{\mu },{\mathbf{\gamma }}^{T}1=\mathbf{\nu }\right\}$

OT:
$$\mathcal{W}(\mathbf{\mu },\mathbf{\nu })=\underset{\gamma \in \Gamma }{\min }⟨\mathbf{C},\gamma ⟩$$

$$\begin{array}{rl}\mathcal{W}(\mathbf{\mu },\mathbf{\nu })& =\underset{\mathbf{\alpha },\mathbf{\beta }\in {\mathbb{R}}^n}{\max }⟨\mathbf{\alpha },\mathbf{\mu }⟩+⟨\mathbf{\beta },\mathbf{\nu }⟩\\ & \text{ s.t. }{\alpha }_i+{\beta }_j\le c\left({\mathbf{x}}_i,{\mathbf{y}}_j\right),\forall i,j\end{array}$$

DM-count

设预测的density map为$\hat{\mathbf{z}}\in {\mathbb{R}}_{+}^n$
gt的density map为$\mathbf{z}\in {\mathbb{R}}_{+}^n$

count loss

这里count loss的作用：因为OT算的归一化的density map，他没有数量信息

${\ell }_C(\mathbf{z},\hat{\mathbf{z}})=\left|\Vert \mathbf{z}{\Vert }_1-\Vert \hat{\mathbf{z}}{\Vert }_1\right|$
由于$\mathbf{z},\hat{\mathbf{z}}\ge 0,$,可以用求和代替1范数
即
${\ell }_C(\mathbf{z},\hat{\mathbf{z}})=\left|{\sum }_{i=1}^n{\mathbf{z}}_i-{\sum }_{i=1}^n{\hat{\mathbf{z}}}_i\right|$

OT loss

$${\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})=\mathcal{W}\left(\frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1},\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\right)=⟨{\mathbf{\alpha }}^{\ast },\frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}⟩+⟨{\mathbf{\beta }}^{\ast },\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}⟩$$
其中${\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }$为OT的对偶问题的最优解
代价矩阵用的是$c(\mathbf{z}(i),\hat{\mathbf{z}}(j))=\Vert \mathbf{z}(i)-\hat{\mathbf{z}}(j){\Vert }_2^2$

$$\frac{\partial {\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})}{\partial \hat{\mathbf{z}}}=\frac{{\mathbf{\beta }}^{\ast }}{\Vert \hat{\mathbf{z}}{\Vert }_1}-\frac{⟨{\mathbf{\beta }}^{\ast },\hat{\mathbf{z}}⟩}{\Vert \hat{\mathbf{z}}{\Vert }_1^2}$$

要注意一个问题，代码里，它的OT loss是

$${\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})=⟨\frac{\partial {\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})}{\partial \hat{\mathbf{z}}},\hat{\mathbf{z}}⟩$$

https://github.com/cvlab-stonybrook/DM-Count/issues/29

求解OT,用的最原始的sinkhorn（没有log-domain

TV loss

这里主要是为了稳定结果

$${\ell }_{TV}(\mathbf{z},\hat{\mathbf{z}})={\Vert \frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}-\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\Vert }_{TV}=\frac{1}{2}{\Vert \frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}-\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\Vert }_1$$

结果

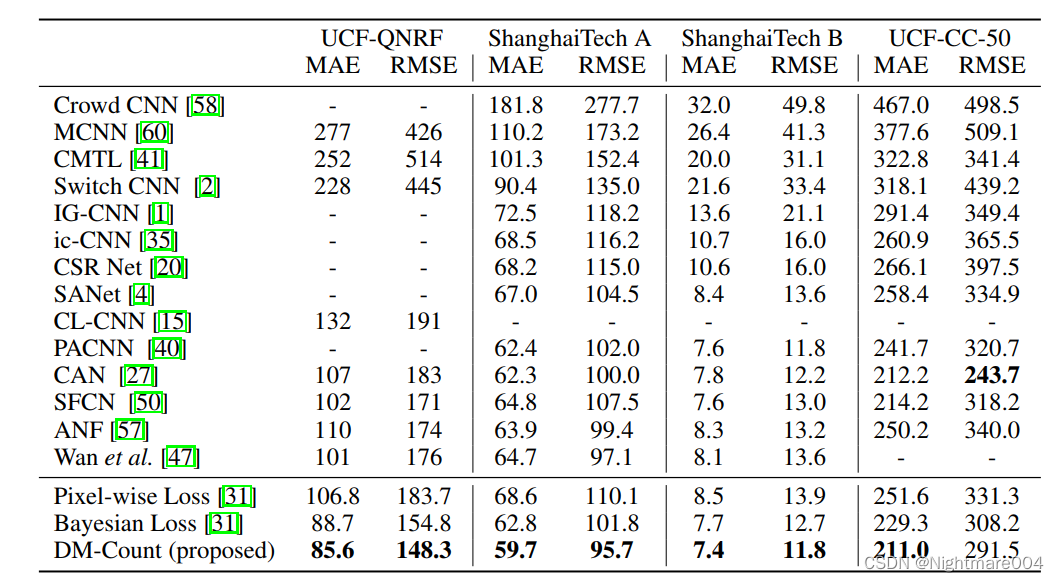
在UCF-QNRF上
作者模型: mae 85.76006602669905, mse 150.3385868782564
我跑的：best_model_7.pth: mae 89.24010239104311, mse 155.59441664755747