数学建模——带相变材料的低温防护服御寒仿真模拟

问题描述

在一些特定的场合，人们往往需要在极寒天气下作业，如高山高原工作、潜水员水下工作、现代化工厂的低温车间以及寒冷气候下的野外作业等。为了能使工作顺利进行，科学家们一直在研究低温防护复合材料，试图做成防护服用以保护在超低温环境下的工作者。

某研究所研制的低温防护复合材料：三层结构，包括内层织物层、中间层功能层、外层隔热层。内层织物层主要用于舒适性。中间层是一种特殊的材料，可以产生并释放热量，用以延缓人体温度过快降低，称为相变材料。外层隔热层主要是延缓热量对外过快传递。低温防护材料主要用于短时间的低温防护，有效降低外界环境对人体的伤害。

为了延缓人体温度过快降低，研制的复合材料的中间层要具有良好的保温性能。中间层有两个特性，特性一是厚度不能大于 0.45mm，因为中间层的硬度与厚度成正比，一旦超过 0.45mm，人体将无法伸展，也就无法工作。特性二是在高于 25℃左右（根据材料不同这个临界点会有小的变化）为液态，低于 25℃开始固化，固化时就开始放热，一直到 14.7℃左右固化完毕，将不再放热。具体数据详见附件 1。注意：附件 1 中的数据放热温度范围与上面表述温度范围有差异，以附件数据为准。

热量传递方式有对流、辐射和传导三种。但在超低温下，对外辐射微不足道，因此一般不予考虑。内层织物与人体表面之间有空气流动，外层隔热层与外部环境之间也有空气流动。空气流速不一样，所计算出来的表面换热系数也会不一样。至于热传导能力（热导率），是材料的物理属性。附件 2 给出了三层材料的物理属性值。

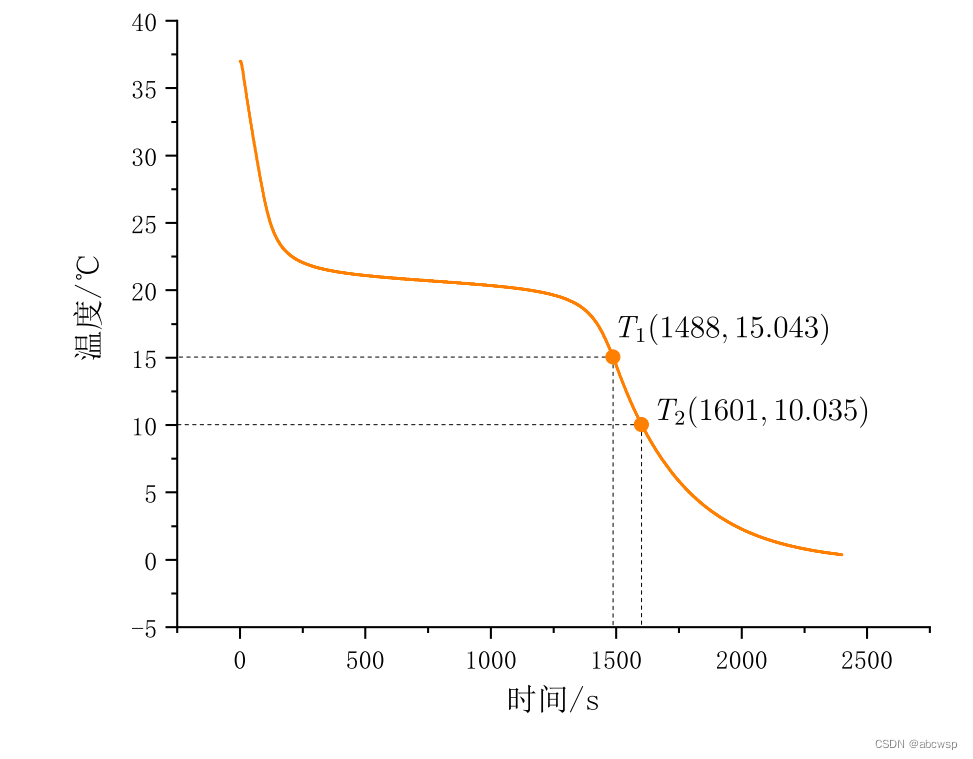
为检验这种复合材料的耐低温效果，科研者按照附件 2 提供的厚度为一名身高 1.70m，体重为 60kg 的中国实验者(消耗的衣料面积一般不超过人体表面积的1.25 倍)制作了一套耐低温服装。实验者将前往南极洲长城站在-40℃的低温下进行工作实验。一般来讲，人体表面温度低于 15℃工作将很困难，低于 10℃将有生命危险。科研者为慎重起见，希望在去南极洲实验前先做仿真模拟。
请你查询和阅读相关资料，运用数学模型，回答下列问题：

问题1：假设实验者站在南极洲长城站附近。当时环境安静，晴天无风，-40℃。请你利用传热学原理对低温防护复合材料在低温环境下传热机理进行分析，建立热量传递数学模型。并预测实验者能够在室外坚持多久？

问题2：假设长城站外面风速为 3m/s，实验者做轻微运动。如何改进第一问的模型，并计算实验者大约多久后就必须要返回室内？

问题3：在问题一的室外环境下，实验者静止不动，实验者穿着较重的防护服，最大承受重量为 100kg。并且每多承受 10s 的时间，最大承受重量将下降0.5kg。如果实验室在低温防护服材料原有支出的基础上能够增加 50%以内的资金，请问如何增加防护服的厚度，使得实验者在外站立时间尽可能的长?

问题4：接着问题三，假定不追加资金，要想提高在户外活动时间，可以通过提高复合材料中间层的放热能力来实现，这是一个新的研究课题。那么，中间功能层的放热能力要比原先提高多少，才能使得实验者在室外坚持的时间不比第三问中坚持的时间少？假定放热能力的提高是在各个温度下同比例增加的。

符号说明

三层耦合抛物型方程

• 固相传热三层耦合模型
  考虑到3层防护复合材料的热传导率、比热以及密度的不同，在功能层未发生固化放热时，根据式\ref{t}对隔热层和织物层分别建立一维热传导方程：
  KaTeX parse error: Undefined control sequence: \label at position 14: \begin{align}\̲l̲a̲b̲e̲l̲{p} \display…
• 相变传热三层耦合模型
  考虑到当功能层温度在14.7~25℃时才放发生固化放热现象，此时热量守恒方程建立在式\ref{p}的功能层上添加一项内热源：
  $$\begin{array}{r}{c}_2{\rho }_2\frac{\partial u_2\left(x,t\right)}{\partial t}=k_2\cdot \frac{{\partial }^2{u}_2\left(x,t\right)}{\partial x^2}+\Phi \left(u_2\right),\end{array}$$

内热源模型

内热源$\Phi \left(u_2\right)$是单位时间单位体积的放热量，DSC是对内热源放热能力的描述。设DSC随温度的拟合方程为$F(T)$，则：
$$\begin{array}{r}\Phi \left(u_2\right)=\frac{\Delta Q}{\Delta t\cdot V}=\frac{mF\left(u_2\right)\Delta t}{\Delta t\cdot V}=F\left(u_2\right){\rho }_2\end{array}$$

初边值条件

• 耦合条件
  根据Fourier热传导定律，在导热过程中，两相邻防护复合材料临界面${\Gamma }_i$处热流量密度$\vec{q}$相同，得到热流量密度耦合条件:
  $$\begin{array}{r}{k}_i\frac{\partial u_i\left(x,t\right)}{\partial n_i}{|}_{{\Gamma }_i}=k_{i+1}\frac{\partial u_{i+1}\left(x,t\right)}{\partial n_{i+1}}{|}_{{\Gamma }_i},i=2or3,\end{array}$$
  由任意时刻下相邻材料临界面${\Gamma }_i$温度相等，从而得到导体传热的临界面温度耦合条件：
  $$\begin{array}{r}{u}_i\left(x,t\right){|}_{{\Gamma }_i}=u_{i+1}\left(x,t\right){|}_{{\Gamma }_i},i=2or3,\end{array}$$
• 第三类边界条件
  由附件中的对流热量公式可得外界与隔热层、皮肤与织物层对流热密度方程：
  $$\begin{array}{r}q=h_c\left(u_1-u_2\right)\end{array}$$
  根据傅里叶热传导定律得到边界处对流热密度方程：
  $$\begin{array}{r}q=-k_i\frac{\partial u_i\left(x,t\right)}{\partial x}{|}_{{\Gamma }_i},i=1or4,\end{array}$$
  联立式（5）、(6)得到热传导方程的第三类边界条件：
  $$\begin{array}{r}\{\begin{array}{l}-k_1\frac{\partial u_1\left(x,t\right)}{\partial x}{|}_{{\Gamma }_1}=h_c\left(T_{ren}-u_1\left(x,t\right){|}_{{\Gamma }_1}\right)\\ -k_3\frac{\partial u_3\left(x,t\right)}{\partial x}{|}_{{\Gamma }_4}=h_c\left(u_3\left(x,t\right){|}_{{\Gamma }_3}-T_{out}\right)\end{array}\end{array}$$
• 初值条件
  将各层材料初始温度设为$T_{ren}=310K$作为初值条件：
  $$\begin{array}{r}{u}_i\left(x,0\right)=T_{ren},i=1\cdots 3.\end{array}$$
  最终整理上述公式得到初边值问题的非线性热传导方程：
  $$\begin{array}{r}\{\begin{array}{l}{c}_i{\rho }_i\cdot \frac{\partial u_i\left(x,t\right)}{\partial t}=k_i\cdot \frac{{\partial }^2{u}_i\left(x,t\right)}{\partial x^2},i=1or3,\\ c_2{\rho }_2\frac{\partial u_2\left(x,t\right)}{\partial t}=k_2\cdot \frac{{\partial }^2{u}_2\left(x,t\right)}{\partial x^2}+\Phi \left(u_2\right),\\ k_i\frac{\partial u_i\left(x,t\right)}{\partial n_i}{|}_{{\Gamma }_i}=k_{i+1}\frac{\partial u_{i+1}\left(x,t\right)}{\partial n_{i+1}}{|}_{{\Gamma }_i},i=2or3,\\ u_i\left(x,t\right){|}_{{\Gamma }_i}=u_{i+1}\left(x,t\right){|}_{{\Gamma }_i},i=2or3,\\ -k_3\frac{\partial u_3}{\partial x}{|}_{{\Gamma }_4}=h_c\left(T_{ren}-u_1\left(x,t\right){|}_{{\Gamma }_1}\right),\\ -k_1\frac{\partial u_1}{\partial x}{|}_{{\Gamma }_1}=h_c\left(u_3\left(x,t\right){|}_{{\Gamma }_3}-T_{out}\right),\\ u_i\left(x,0\right)=T_{ren},i=1\cdots 3.\end{array}\end{array}$$

模型求解