数学建模–模拟退火算法

数学建模–智能算法

1.简介

智能算法又称现代优化算法，主要是用于求解大量来源于实际的组合最优化问题，主要有模拟退火算法、遗传算法、人工神经网络(前？神经网络）、禁忌搜索算法、蚁群算法、差分进化算法和粒子群算法等.

模拟退火算法

1. 简介

模拟退火算法得益于材料统计力学的研究成果.统计力学表明材料中粒子的不同结构对应于粒子的不同能量水平.在高温条件下，粒子的能量较高，可以自由运动和重新排列.在低温条件下，粒子能量较低.如果从高温开始，非常缓慢地降温(这个过程被称为退火)，粒子就可以在每个温度下达到热平衡.当系统完全被冷却后，最终形成处于低能状态的晶体.

2.数学建模中的模拟退火算法原理

如果用粒子的能量来定义材料的状态，Metropolis算法用一个简单的数学模型描述了退火工程. 假设材料自状态i之下的能量为E(i),那么材料在温度T时从状态 i 进入 状态 j 就遵循如下规律：

1. 如果 E(j)<=E(i) , 接受该状态被转换

2. 如果 E(j)>E(i), 则状态转换以如下概率被接受

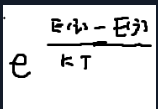
上图中k是物理学中的玻尔兹曼常数，T是材料温度

我们知道，在某一个特定温度下，材料进行了充分的状态转换后，材料将会达到热平衡状态. 这时候材料处于状态 i 的概率将会满足玻尔兹曼分布：

​

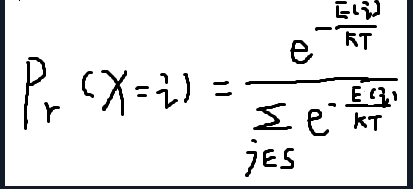
​ X 表示材料当前状态的随机变量，S表示状态空间集合，i表示当前状态，j表示下一个状态

所以 ：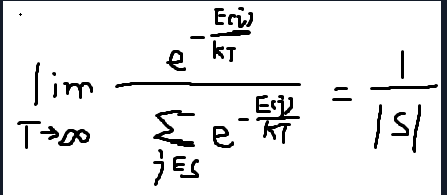
|s| 表示的是集合S中状态的数量，所以我们可以看到在高温下，所有的状态都具有相同的概率，即状态是处于一个均匀分布的状态

而低温时候呢？

上式中

S状态空间最小时候就是只有一个状态i，而这时候 |Smin|=1 , 也就意味着取得 E(i)=Emin的概率为1

这说明了什么呢？ 也就说当温度降至很低时，材料将会以极大的概率能够进入最小能量状态.

如果温度下降十分缓慢，而在每个温度都能够有足够多次的状态转移，使之在每一个温度下都能达到热平衡，则全局最优解将以概率1被找到.

也就是说，温度越低，本身的解也应该更为优化(能力越低), 随着温度越低，该温度下的最优解被找到的概率越大，我们既需要在一个温度下进行多次转换找到该温度下的最优解，也需要不断降低温度，以增加找到最终最优解(最低能量)的概率。

在模拟退火算法中应该注意到以下问题：

1. 理论上，降温过程要足够缓慢，要使得在每一温度下达到热平衡，但在计算机实现中，如果降温速度过缓，所得到的解的性能可能会较为令人满意，但是算法速度会太慢，相对于简单的搜索算法不具有明显优势.而如果降温速度过快，也很可能最终不能找到全局最优解.因此使用时要综合考虑解的性能和算法速度，在两者之间采取一种折中的办法.
2. 要确定在每一温度下状态转换的结束准则.实际操作可以考虑当连续m次的转换过程没有使状态发生变化时结束该温度下的状态转换，最终温度的确定可以提前定为一个较小的温度Te，或者连续几个温度下转换过程没有使状态发生变化算法就结束.
3. 选择合适的初始温度和科学的确定某个可行解的领域的方法.

3.模拟退火算法流程及应用

1.Metropolis采样算法

输入当前解S和温度T：

1. 令k=0时的当前解为S(0)=s,而在温度T下进行以下步骤.

2. 按某一规定方式根据当前解s(k)所处的状态s，产生一个邻近子集N(s(k)),由N(s(k))随机产生一个新的状态**s’**作为一个当前解的候选解，取评价函数C(·),计算

   ​
   $$\Delta C^{\prime }’=C(S^{\prime })-C(s(k)).$$

3. 若ΔC’’<0,则接受s’‘作为下一个当前解;若ΔC">0，则按概率
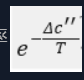
   接受s’作为下一个当前解.

4. 若接受s‘，则令s(k+1)=s’,否则令s(k+1)=s(k).

5. 令k=k+1，判断是否满足收敛准则，不满足则转移到(2); 否则转(6).

6. 返回当前解s(k).

2. 退火过程实现算法

1. 任选一初始状态s0作为初始解 s(0)=s0，并设初始值温度为T0,令i=0.
2. 以Ti和si调用Metropolis采样算法，然后返回当前解si =s.
3. 按一定方式将T降温，令i=i+1，Ti=Ti+ΔT(ΔT<0).
4. 检查退火过程是否结束，若未结束则转移到(2);否则转(5).
5. 以当前解si作为最优解输出.

3.举个栗子

(坐标的由来就是用空间三维直角坐标系去精确表示一个球的表面的所有位置，在表示坐标的时候，需要清楚经度是面面角，某一点的经度，就是该点所在的经线平面与本初子午线平面间的夹角. 而纬度是线面角，某地的纬度就是该地的法线与赤道平面之间的夹角。)

所以A,B两点的实际距离是(根据圆心角和半径求弧长的公式）：

​

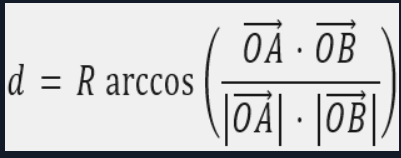
经过化简得到：
$$d=Rarccos[cos(x1-x2)cosy1cosy2+siny1siny2].$$
求解：
主要有以下7个步骤

1. 表示解空间

2. 找目标函数

3. 产生新解

4. 计算代价函数差

5. 以接受准则来接受新的路径

6. 降温**（核心)**

7. 结束条件

8. 

9. 

#程序文件Pex17_1.py
from numpy import loadtxt,radians,sin,cos,inf,exp
from numpy import array,r_,c_,arange,savetxt
from numpy.lib.scimath import arccos
from numpy.random import shuffle,randint,rand
from matplotlib.pyplot import plot, show, rc
a=loadtxt("Pdata17_1.txt")
x=a[:,::2]. flatten(); y=a[:,1::2]. flatten() #这里的数据处理是将所有的经度和维度切出来分别放在两个一维数组中
d1=array([[70,40]]); xy=c_[x,y]   #c_[x,y]将经度和纬度作为横坐标和纵坐标连接在一起构成一个100*2的二维数组  5.37121e+01 表示4.51乘以10的1次方
xy=r_[d1,xy,d1]; N=xy.shape[0]  #r_  加两行数据 70 40 ，现在的N是102 因为初始解有102个数 (0,```,101) 也就是数据矩阵的行数 70 40是我们选择的一个起点
t=radians(xy)  #将坐标数据转化为弧度 方便后面计算距离
d=array([[6370*arccos(cos(t[i,0]-t[j,0])*cos(t[i,1])*cos(t[j,1])+
  sin(t[i,1])*sin(t[j,1])) for i in range(N)]
        for j in range(N)]).real    #real函数返回的是复杂函数的实部，也就是算出的距离的有效值，虽然其实虚部也是0*j
#d是一个102*102的矩阵，存储的是任意102点任意两点的距离
savetxt('Pdata17_2.txt',c_[xy,d])  #把数据保存到文本文件，供下面使用
path=arange(N); L=inf
#Monte Carl方法随机出一个不错的解
for j in range(1000):
    path0=arange(1,N-1); shuffle(path0) #将1000种随机解法乱序
    path0=r_[0,path0,N-1];  L0=d[0,path0[1]]; #首先保证路径能够从起点回到终点 #pathθ是长度为102的一维数组

    #初始化--算出第一种初始解法的路径及距离
    for i in range(1,N-1):
        L0+=d[path0[i],path0[i+1]]
    #通过inf保证循环的第一次一定能够执行成功
    if L0<L:
        path=path0;
        L=L0
print(path,'\n',L)
#到这里，才得到一个不错的path的初始解
#模拟退火算法的核心--进行两万次迭代
e=0.1**30; M=20000; at=0.999; T=1
for k in range(M):
    c=randint(1,101,2); c.sort() #用sort()函数调换顺序
    c1=c[0]; c2=c[1]
    df=d[path[c1-1],path[c2]]+d[path[c1],path[c2+1]]-\
    d[path[c1-1],path[c1]]-d[path[c2],path[c2+1]]  #续行
    if df<0:
        path=r_[path[0],path[1:c1],path[c2:c1-1:-1],path[c2+1:102]]; L=L+df
    else:
        if exp(-df/T)>=rand(1):
            path=r_[path[0],path[1:c1],path[c2:c1-1:-1],path[c2+1:102]]
            L=L+df
    T=T*at
    if T<e: break
print(path,'\n',L)  #输出巡航路径及路径长度
xx=xy[path,0]; yy=xy[path,1]; rc('font',size=16)
plot(xx,yy,'-*'); show()  #画巡航路径

输出如下：

[  0  84  89  56  97  85  81  26  36  79   7  43  55  18  49  57  28  99
  90  98  88  76  63  64  87  47  19   9  32  50  92  73   6  37  46  80
  86  74   2  38  83  69  61  27  44  31  25  93  71   5   1   8  82  60
  58  48   3  15  29  21  59  30  42  45  67  23  51  62  12  68  13  40
  95  77  39  53  78  91  94  11  66  20  10   4  65  96  17  72  75  16
  52  33  14 100  24  34  22  41  70  54  35 101] 
 226404.78269584404
[  0  34  76   3  77  92 100  98  62  53  35  13  26  95  11  29  94  16
  88  46  70  96  19  15  80  17  52   7  41  22  42  79  21  81  20  27
  85  67  93  90   6  23  48  39  89  45  87   9  58  60  57   8  82  50
  25  40  97  10  30  56  59  43  47  69  75  72  36  55  51  37  71  99
  12   4  18  84  54  65  32  33   2  49  83  86  24  14  73  91  28  44
  74  63   1  64  31  78  68  66  38   5  61 101] 
 45168.63607837544

Process finished with exit code 0

图像：

代码需要的相关数据文件可以查看我上传的资源