数据结构：复杂度分析

/* for 循环 */
int forLoop(int n) {
    int res = 0;
    // 循环求和 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        res += i;
    }
    return res;
}

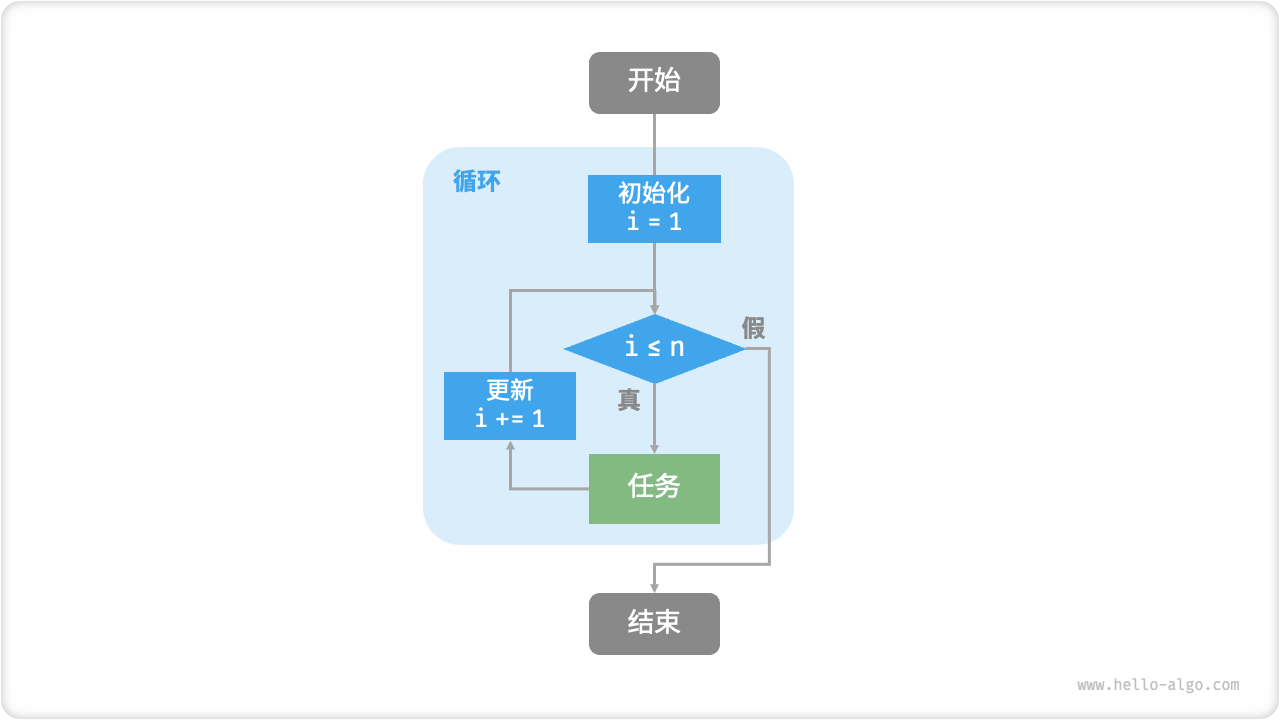
图 2-1 展示了该求和函数的流程框图。

图 2-1 求和函数的流程框图

此求和函数的操作数量与输入数据大小 n成正比，或者说成“线性关系”。实际上，时间复杂度描述的就是这个“线性关系”。相关内容将会在下一节中详细介绍。

2. while 循环

与 for 循环类似，while 循环也是一种实现迭代的方法。在 while 循环中，程序每轮都会先检查条件，如果条件为真则继续执行，否则就结束循环。

下面，我们用 while 循环来实现求和 1+2+⋯+�n。

/* while 循环 */
int whileLoop(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 2, ..., n-1, n
    while (i <= n) {
        res += i;
        i++; // 更新条件变量
    }
    return res;
}

在 while 循环中，由于初始化和更新条件变量的步骤是独立在循环结构之外的，因此它比 for 循环的自由度更高。

例如在以下代码中，条件变量 i 每轮进行了两次更新，这种情况就不太方便用 for 循环实现。

/* while 循环（两次更新） */
int whileLoopII(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 4, ...
    while (i <= n) {
        res += i;
        // 更新条件变量
        i++;
        i *= 2;
    }
    return res;
}

总的来说，for 循环的代码更加紧凑，while 循环更加灵活，两者都可以实现迭代结构。选择使用哪一个应该根据特定问题的需求来决定。

3. 嵌套循环

我们可以在一个循环结构内嵌套另一个循环结构，以 for 循环为例：

/* 双层 for 循环 */
char *nestedForLoop(int n) {
    // n * n 为对应点数量，"(i, j), " 对应字符串长最大为 6+10*2，加上最后一个空字符 \0 的额外空间
    int size = n * n * 26 + 1;
    char *res = malloc(size * sizeof(char));
    // 循环 i = 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        // 循环 j = 1, 2, ..., n-1, n
        for (int j = 1; j <= n; j++) {
            char tmp[26];
            snprintf(tmp, sizeof(tmp), "(%d, %d), ", i, j);
            strncat(res, tmp, size - strlen(res) - 1);
        }
    }
    return res;
}

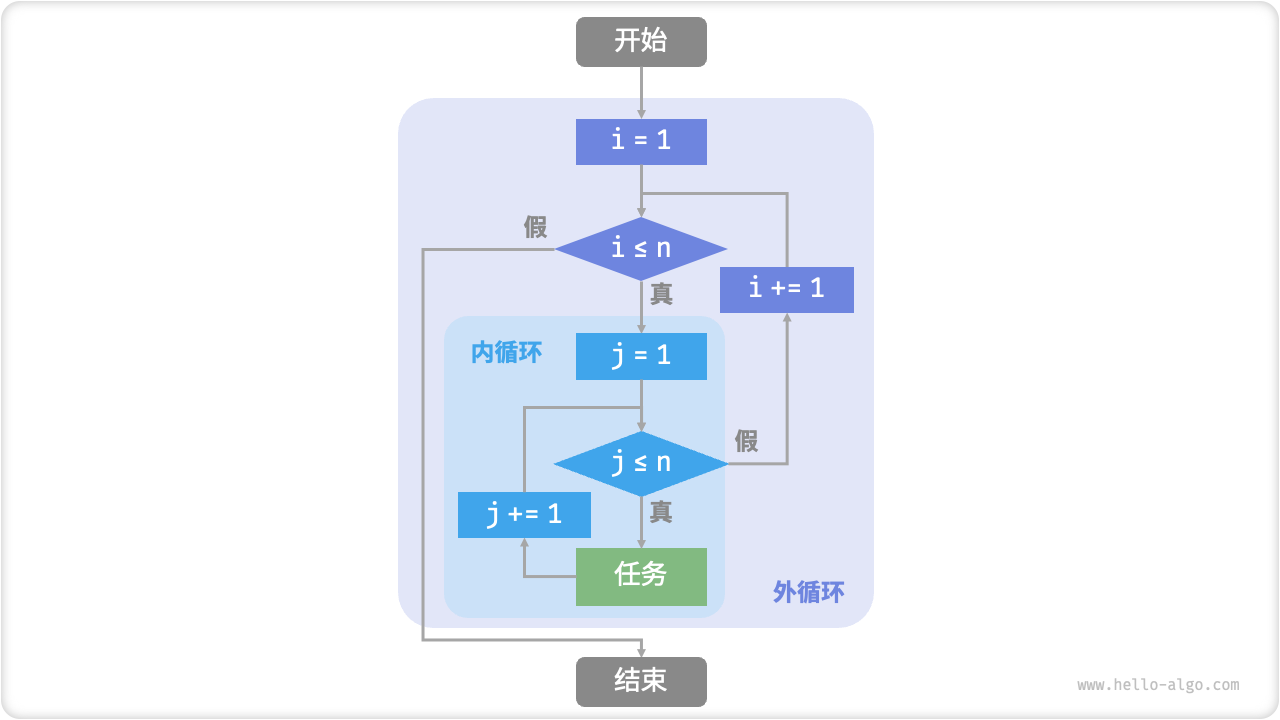
图 2-2 给出了该嵌套循环的流程框图。

图 2-2 嵌套循环的流程框图

在这种情况下，函数的操作数量与 �2 成正比，或者说算法运行时间和输入数据大小 � 成“平方关系”。

我们可以继续添加嵌套循环，每一次嵌套都是一次“升维”，将会使时间复杂度提高至“立方关系”、“四次方关系”、以此类推。

2.2 递归

「递归 recursion」是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。

递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。
归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

而从实现的角度看，递归代码主要包含三个要素。

终止条件：用于决定什么时候由“递”转“归”。
递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
返回结果：对应“归”，将当前递归层级的结果返回至上一层。

观察以下代码，我们只需调用函数 recur(n) ，就可以完成 1+2+⋯+n 的计算：

/* 递归 */
int recur(int n) {
    // 终止条件
    if (n == 1)
        return 1;
    // 递：递归调用
    int res = recur(n - 1);
    // 归：返回结果
    return n + res;
}

图 2-3 展示了该函数的递归过程。

图 2-3 求和函数的递归过程

虽然从计算角度看，迭代与递归可以得到相同的结果，但它们代表了两种完全不同的思考和解决问题的范式。

迭代：“自下而上”地解决问题。从最基础的步骤开始，然后不断重复或累加这些步骤，直到任务完成。
递归：“自上而下”地解决问题。将原问题分解为更小的子问题，这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题，直到基本情况时停止（基本情况的解是已知的）。

以上述的求和函数为例，设问题 f(n)=1+2+⋯+n 。

迭代：在循环中模拟求和过程，从 1 遍历到 �n，每轮执行求和操作，即可求得 f(n) 。
递归：将问题分解为子问题 f(n)=n+f(n−1) ，不断（递归地）分解下去，直至基本情况 f(1)=1 时终止。

1. 调用栈

递归函数每次调用自身时，系统都会为新开启的函数分配内存，以存储局部变量、调用地址和其他信息等。这将导致两方面的结果。

函数的上下文数据都存储在称为“栈帧空间”的内存区域中，直至函数返回后才会被释放。因此，递归通常比迭代更加耗费内存空间。
递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。

如图 2-4 所示，在触发终止条件前，同时存在 n 个未返回的递归函数，递归深度为 n 。

图 2-4 递归调用深度

在实际中，编程语言允许的递归深度通常是有限的，过深的递归可能导致栈溢出报错。

2. 尾递归

有趣的是，如果函数在返回前的最后一步才进行递归调用，则该函数可以被编译器或解释器优化，使其在空间效率上与迭代相当。这种情况被称为「尾递归 tail recursion」。

普通递归：当函数返回到上一层级的函数后，需要继续执行代码，因此系统需要保存上一层调用的上下文。
尾递归：递归调用是函数返回前的最后一个操作，这意味着函数返回到上一层级后，无需继续执行其他操作，因此系统无需保存上一层函数的上下文。

以计算 1+2+⋯+n 为例，我们可以将结果变量 res 设为函数参数，从而实现尾递归。

/* 尾递归 */
int tailRecur(int n, int res) {
    // 终止条件
    if (n == 0)
        return res;
    // 尾递归调用
    return tailRecur(n - 1, res + n);
}

尾递归的执行过程如图 2-5 所示。对比普通递归和尾递归，求和操作的执行点是不同的。

普通递归：求和操作是在“归”的过程中执行的，每层返回后都要再执行一次求和操作。
尾递归：求和操作是在“递”的过程中执行的，“归”的过程只需层层返回。

图 2-5 尾递归过程

Tip

请注意，许多编译器或解释器并不支持尾递归优化。例如，Python 默认不支持尾递归优化，因此即使函数是尾递归形式，但仍然可能会遇到栈溢出问题。

3. 递归树

当处理与“分治”相关的算法问题时，递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例。

Question

给定一个斐波那契数列 0,1,1,2,3,5,8,13,… ，求该数列的第 � 个数字。

设斐波那契数列的第 n个数字为 f(n) ，易得两个结论。

数列的前两个数字为 f(1)=0 和 f(2)=1 。
数列中的每个数字是前两个数字的和，即 f(n)=f(n−1)+f(n−2) 。

按照递推关系进行递归调用，将前两个数字作为终止条件，便可写出递归代码。调用 fib(n) 即可得到斐波那契数列的第 n 个数字。

/* 斐波那契数列：递归 */
int fib(int n) {
    // 终止条件 f(1) = 0, f(2) = 1
    if (n == 1 || n == 2)
        return n - 1;
    // 递归调用 f(n) = f(n-1) + f(n-2)
    int res = fib(n - 1) + fib(n - 2);
    // 返回结果 f(n)
    return res;
}

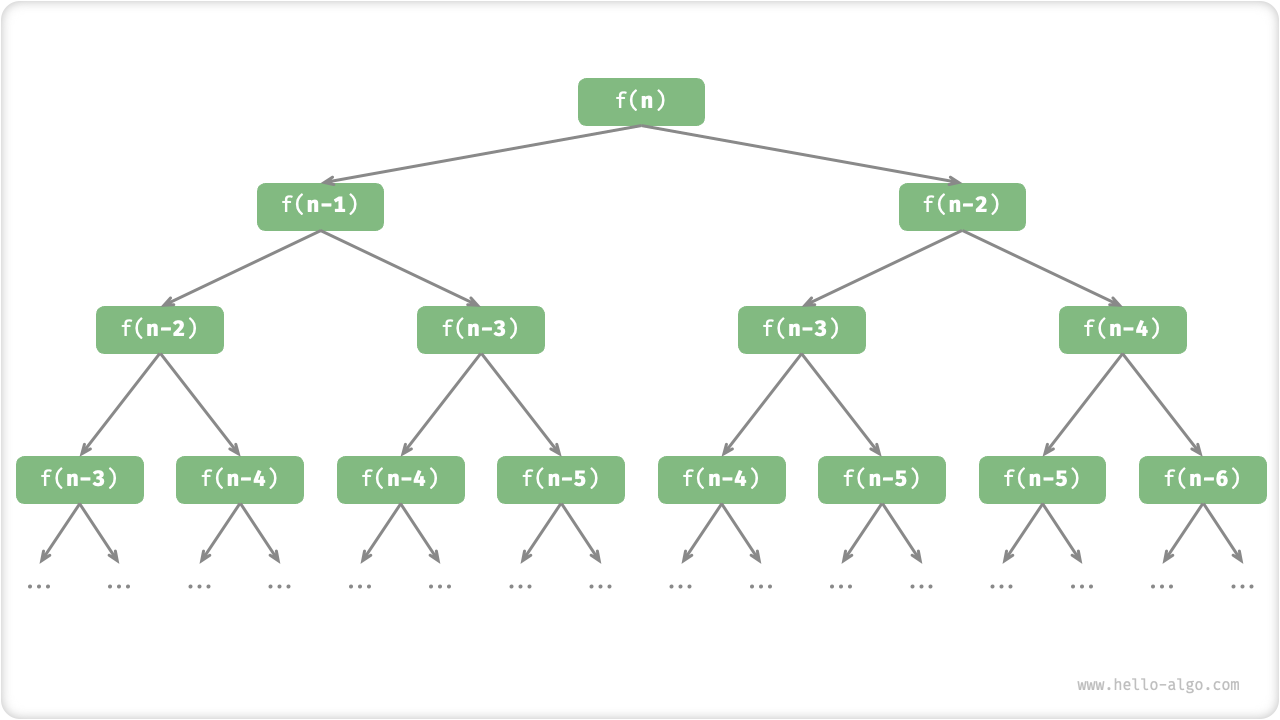
观察以上代码，我们在函数内递归调用了两个函数，这意味着从一个调用产生了两个调用分支。如图 2-6 所示，这样不断递归调用下去，最终将产生一个层数为 n 的「递归树 recursion tree」。

图 2-6 斐波那契数列的递归树

本质上看，递归体现“将问题分解为更小子问题”的思维范式，这种分治策略是至关重要的。

从算法角度看，搜索、排序、回溯、分治、动态规划等许多重要算法策略都直接或间接地应用这种思维方式。
从数据结构角度看，递归天然适合处理链表、树和图的相关问题，因为它们非常适合用分治思想进行分析。

2.3 两者对比

总结以上内容，如表 2-1 所示，迭代和递归在实现、性能和适用性上有所不同。

表 2-1 迭代与递归特点对比

	迭代	递归
实现方式	循环结构	函数调用自身
时间效率	效率通常较高，无函数调用开销	每次函数调用都会产生开销
内存使用	通常使用固定大小的内存空间	累积函数调用可能使用大量的栈帧空间
适用问题	适用于简单循环任务，代码直观、可读性好	适用于子问题分解，如树、图、分治、回溯等，代码结构简洁、清晰

Tip

如果感觉以下内容理解困难，可以在读完“栈”章节后再来复习。

那么，迭代和递归具有什么内在联系呢？以上述的递归函数为例，求和操作在递归的“归”阶段进行。这意味着最初被调用的函数实际上是最后完成其求和操作的，这种工作机制与栈的“先入后出”原则是异曲同工的。

事实上，“调用栈”和“栈帧空间”这类递归术语已经暗示了递归与栈之间的密切关系。

递：当函数被调用时，系统会在“调用栈”上为该函数分配新的栈帧，用于存储函数的局部变量、参数、返回地址等数据。
归：当函数完成执行并返回时，对应的栈帧会从“调用栈”上被移除，恢复之前函数的执行环境。

因此，我们可以使用一个显式的栈来模拟调用栈的行为，从而将递归转化为迭代形式：

[class]{}-[func]{forLoopRecur}

观察以上代码，当递归被转换为迭代后，代码变得更加复杂了。尽管迭代和递归在很多情况下可以互相转换，但也不一定值得这样做，有以下两点原因。

转化后的代码可能更加难以理解，可读性更差。
对于某些复杂问题，模拟系统调用栈的行为可能非常困难。

总之，选择迭代还是递归取决于特定问题的性质。在编程实践中，权衡两者的优劣并根据情境选择合适的方法是至关重要的。

3 时间复杂度

运行时间可以直观且准确地反映算法的效率。如果我们想要准确预估一段代码的运行时间，应该如何操作呢？

确定运行平台，包括硬件配置、编程语言、系统环境等，这些因素都会影响代码的运行效率。
评估各种计算操作所需的运行时间，例如加法操作 + 需要 1 ns ，乘法操作 * 需要 10 ns ，打印操作 print() 需要 5 ns 等。
统计代码中所有的计算操作，并将所有操作的执行时间求和，从而得到运行时间。

例如在以下代码中，输入数据大小为 n ：

// 在某运行平台下
void algorithm(int n) {
    int a = 2;  // 1 ns
    a = a + 1;  // 1 ns
    a = a * 2;  // 10 ns
    // 循环 n 次
    for (int i = 0; i < n; i++) {   // 1 ns ，每轮都要执行 i++
        printf("%d", 0);            // 5 ns
    }
}

根据以上方法，可以得到算法运行时间为 6n+12 ns ：

1+1+10+(1+5)×n=6n+12

但实际上，统计算法的运行时间既不合理也不现实。首先，我们不希望将预估时间和运行平台绑定，因为算法需要在各种不同的平台上运行。其次，我们很难获知每种操作的运行时间，这给预估过程带来了极大的难度。

3.1 统计时间增长趋势

时间复杂度分析统计的不是算法运行时间，而是算法运行时间随着数据量变大时的增长趋势。

“时间增长趋势”这个概念比较抽象，我们通过一个例子来加以理解。假设输入数据大小为 n ，给定三个算法函数 A、B 和 C ：

// 算法 A 的时间复杂度：常数阶
void algorithm_A(int n) {
    printf("%d", 0);
}
// 算法 B 的时间复杂度：线性阶
void algorithm_B(int n) {
    for (int i = 0; i < n; i++) {
        printf("%d", 0);
    }
}
// 算法 C 的时间复杂度：常数阶
void algorithm_C(int n) {
    for (int i = 0; i < 1000000; i++) {
        printf("%d", 0);
    }
}

图 2-7 展示了以上三个算法函数的时间复杂度。

算法 A 只有 1 个打印操作，算法运行时间不随着 n 增大而增长。我们称此算法的时间复杂度为“常数阶”。
算法 B 中的打印操作需要循环 n次，算法运行时间随着 n增大呈线性增长。此算法的时间复杂度被称为“线性阶”。
算法 C 中的打印操作需要循环 1000000 次，虽然运行时间很长，但它与输入数据大小 n 无关。因此 C 的时间复杂度和 A 相同，仍为“常数阶”。

图 2-7 算法 A、B 和 C 的时间增长趋势

相较于直接统计算法运行时间，时间复杂度分析有哪些特点呢？

时间复杂度能够有效评估算法效率。例如，算法 B 的运行时间呈线性增长，在 n>1 时比算法 A 更慢，在 n>1000000 时比算法 C 更慢。事实上，只要输入数据大小 n足够大，复杂度为“常数阶”的算法一定优于“线性阶”的算法，这正是时间增长趋势所表达的含义。
时间复杂度的推算方法更简便。显然，运行平台和计算操作类型都与算法运行时间的增长趋势无关。因此在时间复杂度分析中，我们可以简单地将所有计算操作的执行时间视为相同的“单位时间”，从而将“计算操作的运行时间的统计”简化为“计算操作的数量的统计”，这样以来估算难度就大大降低了。
时间复杂度也存在一定的局限性。例如，尽管算法 A 和 C 的时间复杂度相同，但实际运行时间差别很大。同样，尽管算法 B 的时间复杂度比 C 高，但在输入数据大小 n较小时，算法 B 明显优于算法 C 。在这些情况下，我们很难仅凭时间复杂度判断算法效率的高低。当然，尽管存在上述问题，复杂度分析仍然是评判算法效率最有效且常用的方法。

3.2 函数渐近上界

给定一个输入大小为 n 的函数：

void algorithm(int n) {
    int a = 1;  // +1
    a = a + 1;  // +1
    a = a * 2;  // +1
    // 循环 n 次
    for (int i = 0; i < n; i++) {   // +1（每轮都执行 i ++）
        printf("%d", 0);            // +1
    }
}

设算法的操作数量是一个关于输入数据大小 n的函数，记为 T(n) ，则以上函数的的操作数量为：

T(n)=3+2n

T(n) 是一次函数，说明其运行时间的增长趋势是线性的，因此它的时间复杂度是线性阶。

我们将线性阶的时间复杂度记为 O(n) ，这个数学符号称为「大 O记号 big-O notation」，表示函数 T(n) 的「渐近上界 asymptotic upper bound」。

时间复杂度分析本质上是计算“操作数量函数 T(n)”的渐近上界，其具有明确的数学定义。

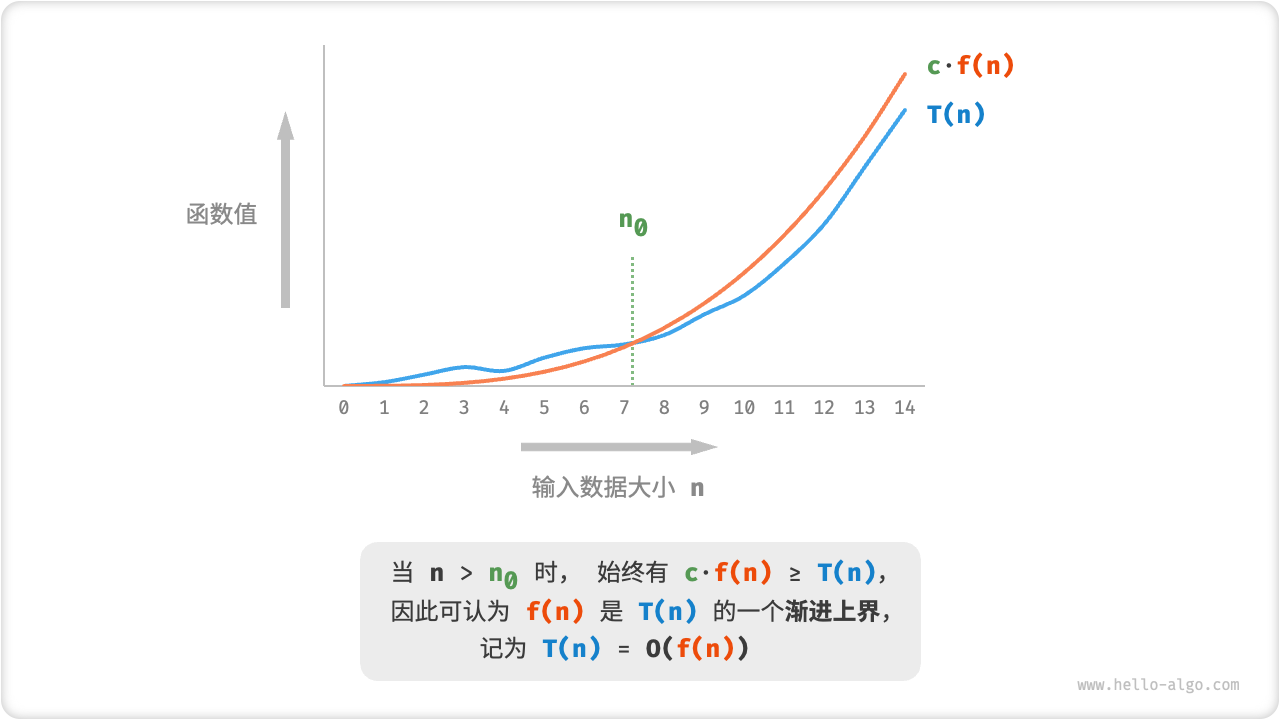
如图 2-8 所示，计算渐近上界就是寻找一个函数 f(n) ，使得当 n趋向于无穷大时，T(n) 和 f(n) 处于相同的增长级别，仅相差一个常数项 c的倍数。

图 2-8 函数的渐近上界

3.3 推算方法

渐近上界的数学味儿有点重，如果你感觉没有完全理解，也无须担心。因为在实际使用中，我们只需要掌握推算方法，数学意义就可以逐渐领悟。

1. 第一步：统计操作数量

针对代码，逐行从上到下计算即可。然而，由于上述 c⋅f(n) 中的常数项 c 可以取任意大小，因此操作数量 f(n) 中的各种系数、常数项都可以被忽略。根据此原则，可以总结出以下计数简化技巧。

忽略 f(n) 中的常数项。因为它们都与 n 无关，所以对时间复杂度不产生影响。
省略所有系数。例如，循环 2n次、5n+1 次等，都可以简化记为 n次，因为 n 前面的系数对时间复杂度没有影响。
循环嵌套时使用乘法。总操作数量等于外层循环和内层循环操作数量之积，每一层循环依然可以分别套用第 1. 点和第 2. 点的技巧。

给定一个函数，我们可以用上述技巧来统计操作数量。

void algorithm(int n) {
    int a = 1;  // +0（技巧 1）
    a = a + n;  // +0（技巧 1）
    // +n（技巧 2）
    for (int i = 0; i < 5 * n + 1; i++) {
        printf("%d", 0);
    }
    // +n*n（技巧 3）
    for (int i = 0; i < 2 * n; i++) {
        for (int j = 0; j < n + 1; j++) {
            printf("%d", 0);
        }
    }
}

2. 第二步：判断渐近上界

时间复杂度由多项式 T(n) 中最高阶的项来决定。这是因为在 n 趋于无穷大时，最高阶的项将发挥主导作用，其他项的影响都可以被忽略。

表 2-2 展示了一些例子，其中一些夸张的值是为了强调“系数无法撼动阶数”这一结论。当 n 趋于无穷大时，这些常数变得无足轻重。

表 2-2 不同操作数量对应的时间复杂度

操作数量	时间复杂度
100000	O(1)
3n+2	O(n)
2n2+3n+2	O(n2)
n3+10000n2	O(n3)
2n+10000n10000	n(2n)

3.4 常见类型

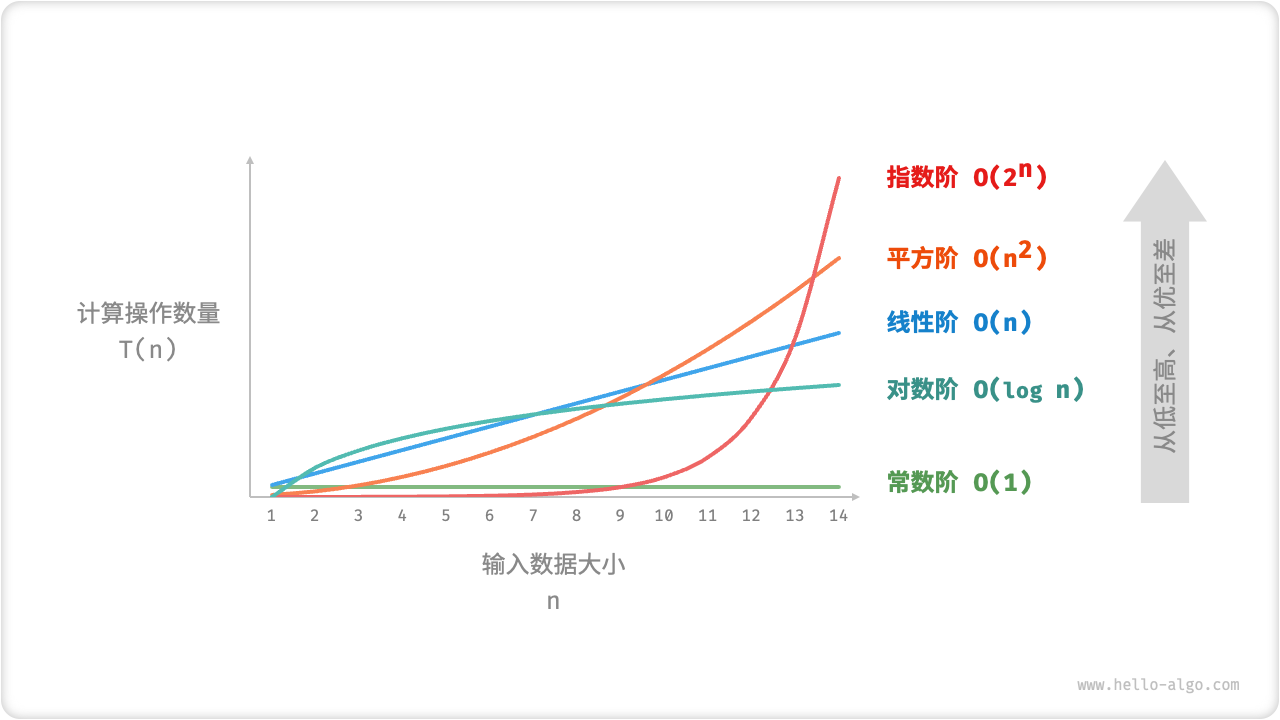
设输入数据大小为 n ，常见的时间复杂度类型如图 2-9 所示（按照从低到高的顺序排列）。

常数阶<对数阶<线性阶<线性对数阶<平方阶<指数阶<阶乘阶

图 2-9 常见的时间复杂度类型

1. 常数阶 O(1)

常数阶的操作数量与输入数据大小 n 无关，即不随着 n 的变化而变化。

在以下函数中，尽管操作数量 size 可能很大，但由于其与输入数据大小 n无关，因此时间复杂度仍为 O(1) ：

/* 常数阶 */
int constant(int n) {
    int count = 0;
    int size = 100000;
    int i = 0;
    for (int i = 0; i < size; i++) {
        count++;
    }
    return count;
}

2. 线性阶 O(n)

线性阶的操作数量相对于输入数据大小 n 以线性级别增长。线性阶通常出现在单层循环中：

/* 线性阶 */
int linear(int n) {
    int count = 0;
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

遍历数组和遍历链表等操作的时间复杂度均为 O(n) ，其中 n 为数组或链表的长度：

/* 线性阶（遍历数组） */
int arrayTraversal(int *nums, int n) {
    int count = 0;
    // 循环次数与数组长度成正比
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

值得注意的是，输入数据大小 n 需根据输入数据的类型来具体确定。

3. 平方阶 O(n2)

平方阶的操作数量相对于输入数据大小 n以平方级别增长。平方阶通常出现在嵌套循环中，外层循环和内层循环都为 O(n) ，因此总体为 O(n2) ：

/* 平方阶 */
int quadratic(int n) {
    int count = 0;
    // 循环次数与数组长度成平方关系
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            count++;
        }
    }
    return count;
}

图 2-10 对比了常数阶、线性阶和平方阶三种时间复杂度。

图 2-10 常数阶、线性阶和平方阶的时间复杂度

以冒泡排序为例，外层循环执行 n−1 次，内层循环执行 n−1、n−2、…、2、1 次，平均为 n/2 次，因此时间复杂度为 n((n−1)n/2)=O(n2) 。

/* 平方阶（冒泡排序） */
int bubbleSort(int *nums, int n) {
    int count = 0; // 计数器
    // 外循环：未排序区间为 [0, i]
    for (int i = n - 1; i > 0; i--) {
        // 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
        for (int j = 0; j < i; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 与 nums[j + 1]
                int tmp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = tmp;
                count += 3; // 元素交换包含 3 个单元操作
            }
        }
    }
    return count;
}

4. 指数阶 O(2n)

生物学的“细胞分裂”是指数阶增长的典型例子：初始状态为 1 个细胞，分裂一轮后变为 2 个，分裂两轮后变为 4 个，以此类推，分裂 n 轮后有 2n 个细胞。

图 2-11 和以下代码模拟了细胞分裂的过程，时间复杂度为 O(2n) 。

/* 指数阶（循环实现） */
int exponential(int n) {
    int count = 0;
    int bas = 1;
    // 细胞每轮一分为二，形成数列 1, 2, 4, 8, ..., 2^(n-1)
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < bas; j++) {
            count++;
        }
        bas *= 2;
    }
    // count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
    return count;
}

图 2-11 指数阶的时间复杂度

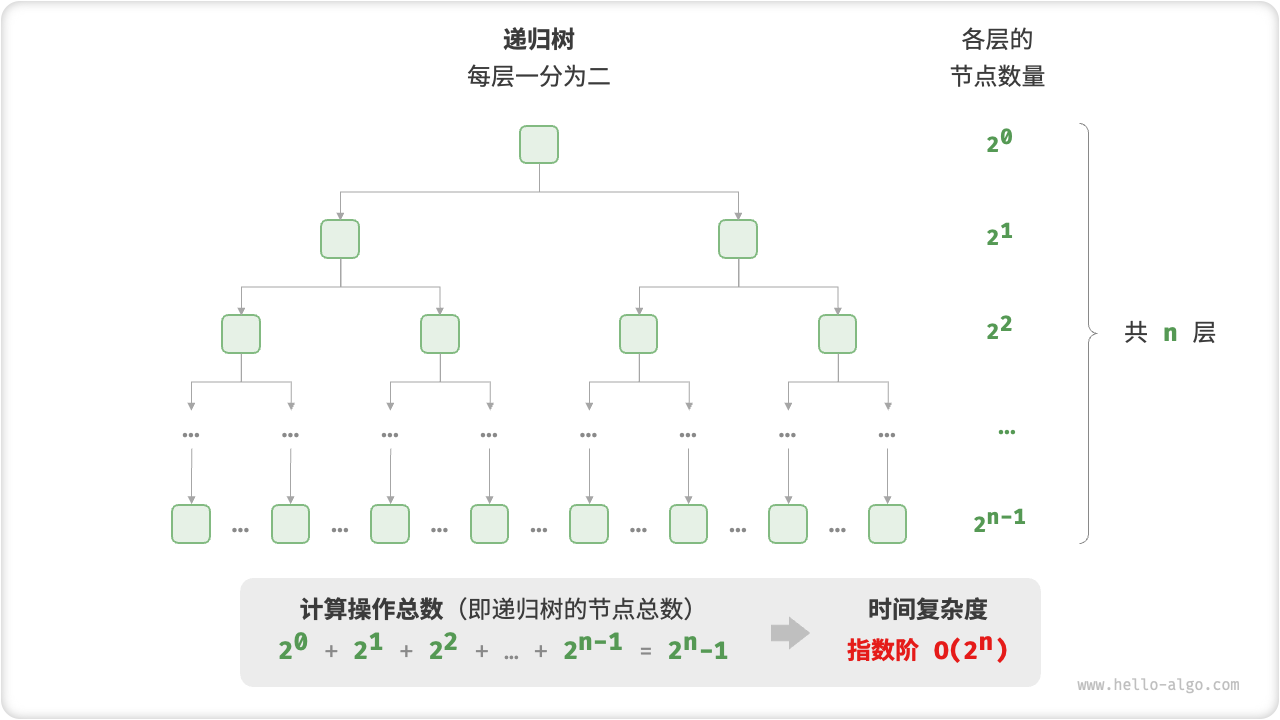
在实际算法中，指数阶常出现于递归函数中。例如在以下代码中，其递归地一分为二，经过 n 次分裂后停止：

/* 指数阶（递归实现） */
int expRecur(int n) {
    if (n == 1)
        return 1;
    return expRecur(n - 1) + expRecur(n - 1) + 1;
}

指数阶增长非常迅速，在穷举法（暴力搜索、回溯等）中比较常见。对于数据规模较大的问题，指数阶是不可接受的，通常需要使用动态规划或贪心等算法来解决。

5. 对数阶 O(log⁡n)

与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 � ，由于每轮缩减到一半，因此循环次数是 log2⁡n ，即 2n 的反函数。

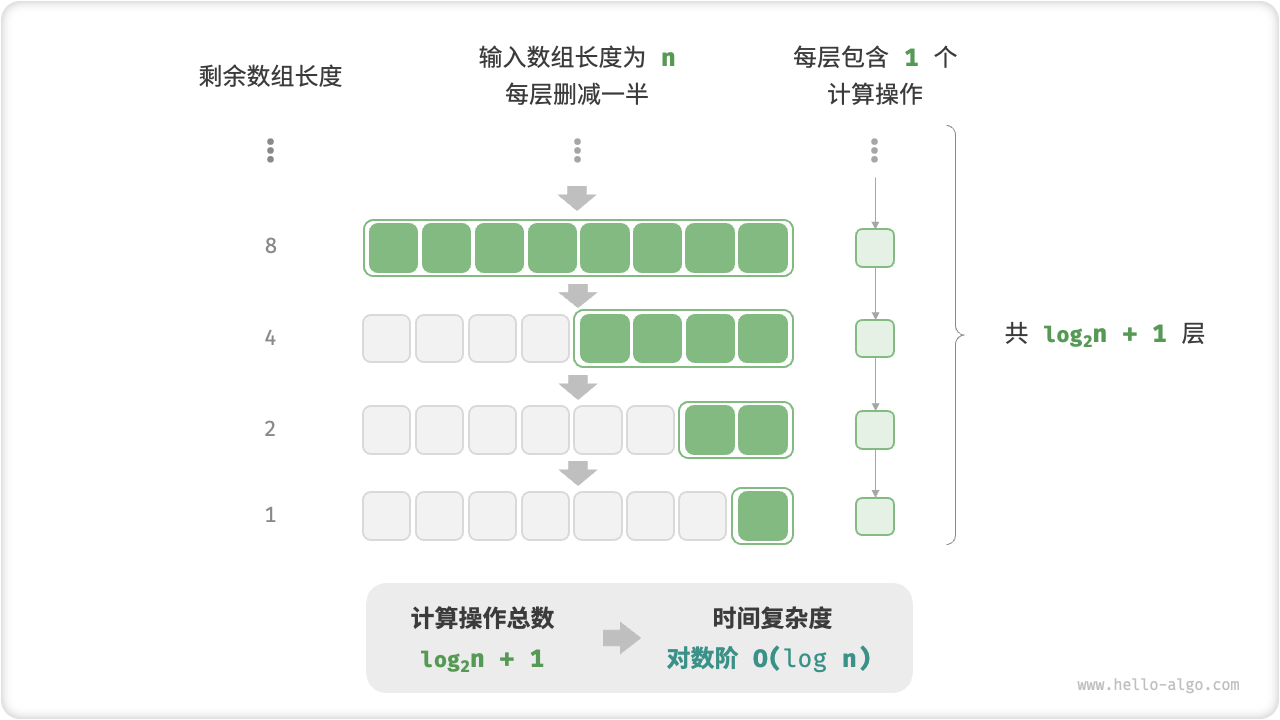
图 2-12 和以下代码模拟了“每轮缩减到一半”的过程，时间复杂度为 O(log2⁡n) ，简记为 O(log⁡n) 。

/* 对数阶（循环实现） */
int logarithmic(float n) {
    int count = 0;
    while (n > 1) {
        n = n / 2;
        count++;
    }
    return count;
}

图 2-12 对数阶的时间复杂度

与指数阶类似，对数阶也常出现于递归函数中。以下代码形成了一个高度为 log2⁡n 的递归树：

/* 对数阶（递归实现） */
int logRecur(float n) {
    if (n <= 1)
        return 0;
    return logRecur(n / 2) + 1;
}

对数阶常出现于基于分治策略的算法中，体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢，是仅次于常数阶的理想的时间复杂度。

6. 线性对数阶 O(nlog⁡n)

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 O(log⁡n) 和 O(n) 。相关代码如下：

/* 线性对数阶 */
int linearLogRecur(float n) {
    if (n <= 1)
        return 1;
    int count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

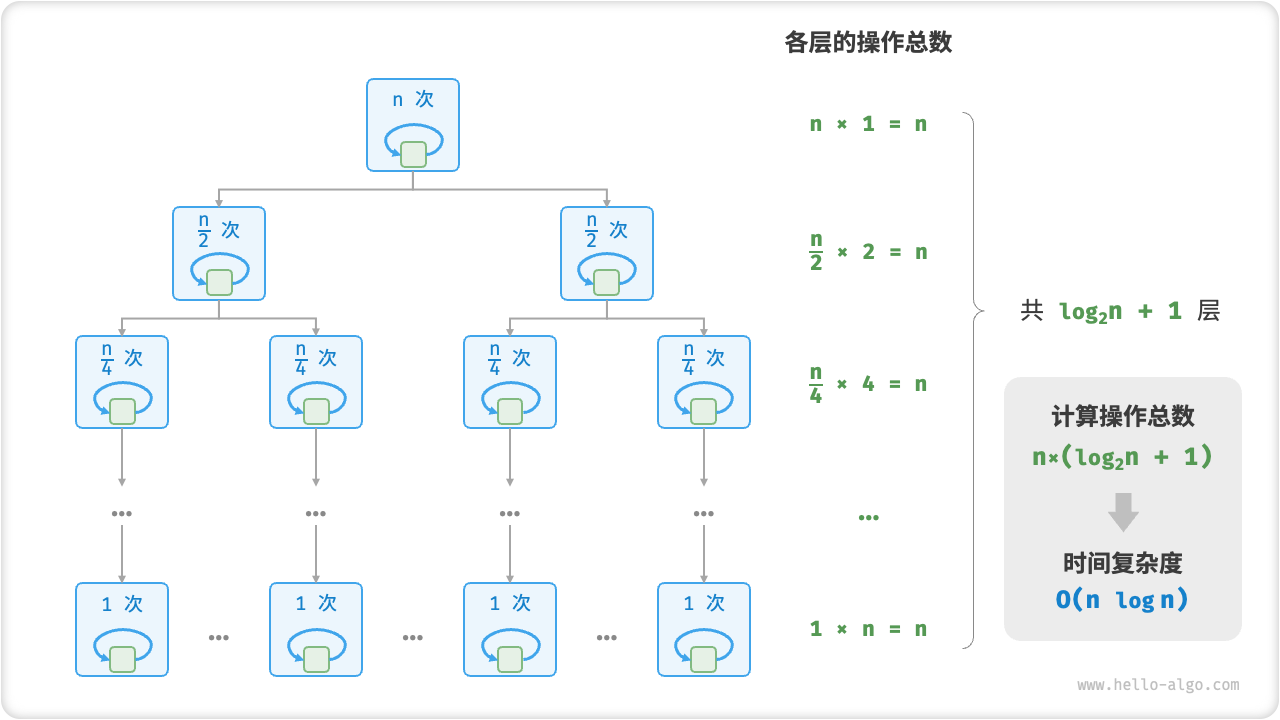
图 2-13 展示了线性对数阶的生成方式。二叉树的每一层的操作总数都为 n ，树共有 log2⁡n+1 层，因此时间复杂度为 O(nlog⁡n) 。

图 2-13 线性对数阶的时间复杂度

主流排序算法的时间复杂度通常为 O(nlog⁡n) ，例如快速排序、归并排序、堆排序等。

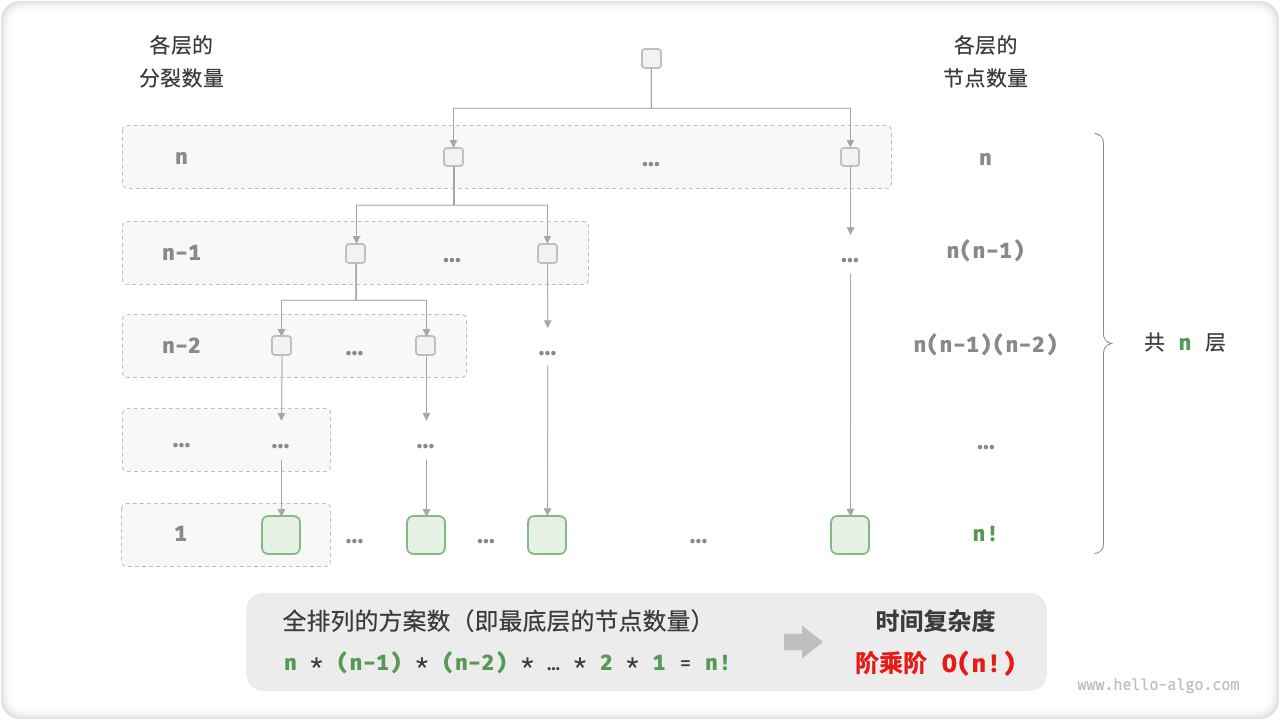
7. 阶乘阶 O(n!)

阶乘阶对应数学上的“全排列”问题。给定 n 个互不重复的元素，求其所有可能的排列方案，方案数量

阶乘通常使用递归实现。如图 2-14 和以下代码所示，第一层分裂出 n 个，第二层分裂出 n−1 个，以此类推，直至第 n 层时停止分裂：

/* 阶乘阶（递归实现） */
int factorialRecur(int n) {
    if (n == 0)
        return 1;
    int count = 0;
    for (int i = 0; i < n; i++) {
        count += factorialRecur(n - 1);
    }
    return count;
}

图 2-14 阶乘阶的时间复杂度

请注意，因为当 n≥4 时恒有 n!>2n ，所以阶乘阶比指数阶增长得更快，在 n 较大时也是不可接受的。

3.5 最差、最佳、平均时间复杂度

算法的时间效率往往不是固定的，而是与输入数据的分布有关。假设输入一个长度为 � 的数组 nums ，其中 nums 由从 1 至 n 的数字组成，每个数字只出现一次；但元素顺序是随机打乱的，任务目标是返回元素 1 的索引。我们可以得出以下结论。

当 nums = [?, ?, ..., 1] ，即当末尾元素是 1 时，需要完整遍历数组，达到最差时间复杂度 O(n) 。
当 nums = [1, ?, ?, ...] ，即当首个元素为 1 时，无论数组多长都不需要继续遍历，达到最佳时间复杂度 Ω(1) 。

“最差时间复杂度”对应函数渐近上界，使用大 O 记号表示。相应地，“最佳时间复杂度”对应函数渐近下界，用 Ω 记号表示：

/* 生成一个数组，元素为 { 1, 2, ..., n }，顺序被打乱 */
int *randomNumbers(int n) {
    // 分配堆区内存（创建一维可变长数组：数组中元素数量为 n ，元素类型为 int ）
    int *nums = (int *)malloc(n * sizeof(int));
    // 生成数组 nums = { 1, 2, 3, ..., n }
    for (int i = 0; i < n; i++) {
        nums[i] = i + 1;
    }
    // 随机打乱数组元素
    for (int i = n - 1; i > 0; i--) {
        int j = rand() % (i + 1);
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    return nums;
}

/* 查找数组 nums 中数字 1 所在索引 */
int findOne(int *nums, int n) {
    for (int i = 0; i < n; i++) {
        // 当元素 1 在数组头部时，达到最佳时间复杂度 O(1)
        // 当元素 1 在数组尾部时，达到最差时间复杂度 O(n)
        if (nums[i] == 1)
            return i;
    }
    return -1;
}

值得说明的是，我们在实际中很少使用最佳时间复杂度，因为通常只有在很小概率下才能达到，可能会带来一定的误导性。而最差时间复杂度更为实用，因为它给出了一个效率安全值，让我们可以放心地使用算法。

从上述示例可以看出，最差或最佳时间复杂度只出现于“特殊的数据分布”，这些情况的出现概率可能很小，并不能真实地反映算法运行效率。相比之下，平均时间复杂度可以体现算法在随机输入数据下的运行效率，用 Θ 记号来表示。

对于部分算法，我们可以简单地推算出随机数据分布下的平均情况。比如上述示例，由于输入数组是被打乱的，因此元素 1 出现在任意索引的概率都是相等的，那么算法的平均循环次数就是数组长度的一半 n/2 ，平均时间复杂度为 Θ(n/2)=Θ(n) 。

但对于较为复杂的算法，计算平均时间复杂度往往是比较困难的，因为很难分析出在数据分布下的整体数学期望。在这种情况下，我们通常使用最差时间复杂度作为算法效率的评判标准。

为什么很少看到 Θ 符号？

可能由于 O符号过于朗朗上口，我们常常使用它来表示平均时间复杂度。但从严格意义上看，这种做法并不规范。在本书和其他资料中，若遇到类似“平均时间复杂度 O(n)”的表述，请将其直接理解为 Θ(n) 。

4 空间复杂度

「空间复杂度 space complexity」用于衡量算法占用内存空间随着数据量变大时的增长趋势。这个概念与时间复杂度非常类似，只需将“运行时间”替换为“占用内存空间”。

4.1 算法相关空间

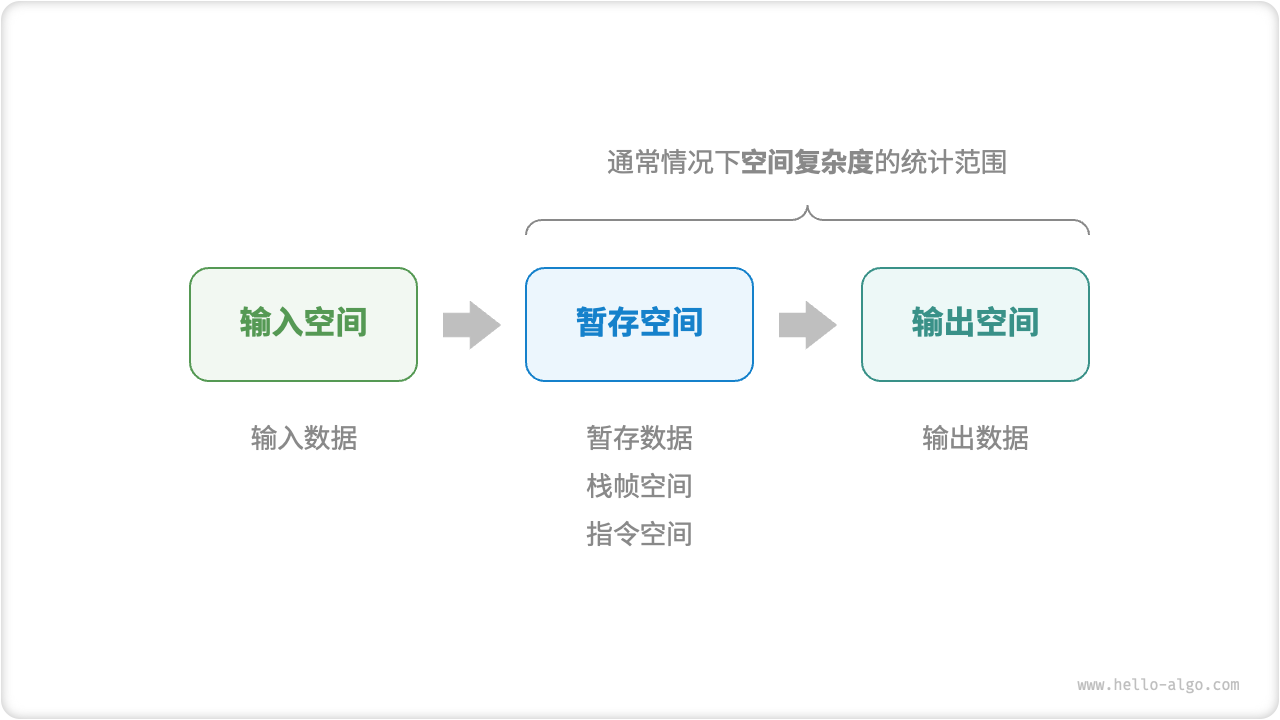
算法在运行过程中使用的内存空间主要包括以下几种。

输入空间：用于存储算法的输入数据。
暂存空间：用于存储算法在运行过程中的变量、对象、函数上下文等数据。
输出空间：用于存储算法的输出数据。

一般情况下，空间复杂度的统计范围是“暂存空间”加上“输出空间”。

暂存空间可以进一步划分为三个部分。

暂存数据：用于保存算法运行过程中的各种常量、变量、对象等。
栈帧空间：用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧，函数返回后，栈帧空间会被释放。
指令空间：用于保存编译后的程序指令，在实际统计中通常忽略不计。

在分析一段程序的空间复杂度时，我们通常统计暂存数据、栈帧空间和输出数据三部分。

图 2-15 算法使用的相关空间

/* 函数 */
int func() {
    // 执行某些操作...
    return 0;
}

int algorithm(int n) { // 输入数据
    const int a = 0;   // 暂存数据（常量）
    int b = 0;         // 暂存数据（变量）
    int c = func();    // 栈帧空间（调用函数）
    return a + b + c;  // 输出数据
}

4.2 推算方法

空间复杂度的推算方法与时间复杂度大致相同，只需将统计对象从“操作数量”转为“使用空间大小”。

而与时间复杂度不同的是，我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。

观察以下代码，最差空间复杂度中的“最差”有两层含义。

以最差输入数据为准：当 n<10 时，空间复杂度为 O(1) ；但当 n>10 时，初始化的数组 nums 占用 O(n) 空间；因此最差空间复杂度为 O(n) 。
以算法运行中的峰值内存为准：例如，程序在执行最后一行之前，占用 O(1) 空间；当初始化数组 nums 时，程序占用 O(n) 空间；因此最差空间复杂度为 O(n) 。

void algorithm(int n) {
    int a = 0;               // O(1)
    int b[10000];            // O(1)
    if (n > 10)
        int nums[n] = {0};   // O(n)
}

在递归函数中，需要注意统计栈帧空间。例如在以下代码中：

函数 loop() 在循环中调用了 n次 function() ，每轮中的 function() 都返回并释放了栈帧空间，因此空间复杂度仍为 O(1) 。
递归函数 recur() 在运行过程中会同时存在 n 个未返回的 recur() ，从而占用 O(n) 的栈帧空间。

int func() {
    // 执行某些操作
    return 0;
}
/* 循环 O(1) */
void loop(int n) {
    for (int i = 0; i < n; i++) {
        func();
    }
}
/* 递归 O(n) */
void recur(int n) {
    if (n == 1) return;
    return recur(n - 1);
}

4.3 常见类型

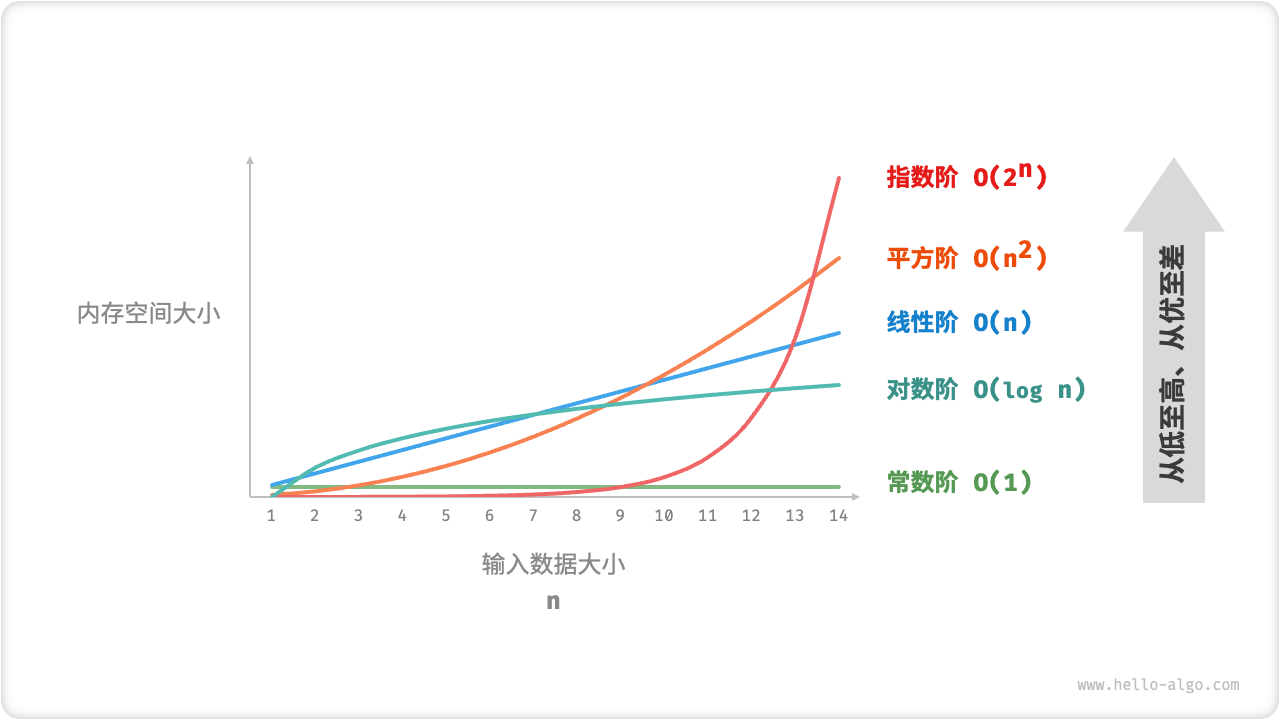
设输入数据大小为 n ，图 2-16 展示了常见的空间复杂度类型（从低到高排列）。

常数阶<对数阶<线性阶<平方阶<指数阶

图 2-16 常见的空间复杂度类型

1. 常数阶 O(1)

常数阶常见于数量与输入数据大小 n无关的常量、变量、对象。

需要注意的是，在循环中初始化变量或调用函数而占用的内存，在进入下一循环后就会被释放，因此不会累积占用空间，空间复杂度仍为 O(1) ：

/* 函数 */
int func() {
    // 执行某些操作
    return 0;
}

/* 常数阶 */
void constant(int n) {
    // 常量、变量、对象占用 O(1) 空间
    const int a = 0;
    int b = 0;
    int nums[1000];
    ListNode *node = newListNode(0);
    free(node);
    // 循环中的变量占用 O(1) 空间
    for (int i = 0; i < n; i++) {
        int c = 0;
    }
    // 循环中的函数占用 O(1) 空间
    for (int i = 0; i < n; i++) {
        func();
    }
}

2. 线性阶 O(n)

线性阶常见于元素数量与 n 成正比的数组、链表、栈、队列等：

/* 哈希表 */
struct hashTable {
    int key;
    int val;
    UT_hash_handle hh; // 基于 uthash.h 实现
};

typedef struct hashTable hashTable;

/* 线性阶 */
void linear(int n) {
    // 长度为 n 的数组占用 O(n) 空间
    int *nums = malloc(sizeof(int) * n);
    free(nums);

    // 长度为 n 的列表占用 O(n) 空间
    ListNode **nodes = malloc(sizeof(ListNode *) * n);
    for (int i = 0; i < n; i++) {
        nodes[i] = newListNode(i);
    }
    // 内存释放
    for (int i = 0; i < n; i++) {
        free(nodes[i]);
    }
    free(nodes);

    // 长度为 n 的哈希表占用 O(n) 空间
    hashTable *h = NULL;
    for (int i = 0; i < n; i++) {
        hashTable *tmp = malloc(sizeof(hashTable));
        tmp->key = i;
        tmp->val = i;
        HASH_ADD_INT(h, key, tmp);
    }

    // 内存释放
    hashTable *curr, *tmp;
    HASH_ITER(hh, h, curr, tmp) {
        HASH_DEL(h, curr);
        free(curr);
    }
}

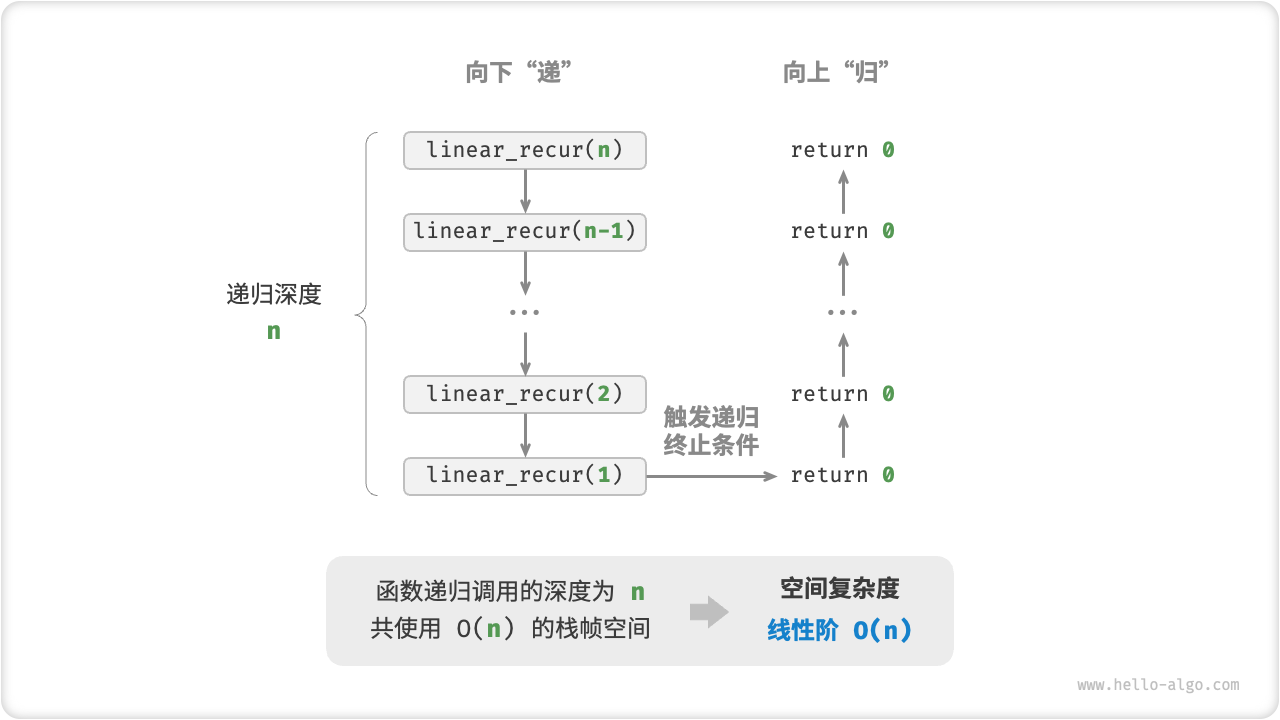
如图 2-17 所示，此函数的递归深度为 n ，即同时存在 n 个未返回的 linear_recur() 函数，使用 O(n) 大小的栈帧空间：

/* 线性阶（递归实现） */
void linearRecur(int n) {
    printf("递归 n = %d\r\n", n);
    if (n == 1)
        return;
    linearRecur(n - 1);
}

图 2-17 递归函数产生的线性阶空间复杂度

3. 平方阶 O(n2)

平方阶常见于矩阵和图，元素数量与 n 成平方关系：

/* 平方阶 */
void quadratic(int n) {
    // 二维列表占用 O(n^2) 空间
    int **numMatrix = malloc(sizeof(int *) * n);
    for (int i = 0; i < n; i++) {
        int *tmp = malloc(sizeof(int) * n);
        for (int j = 0; j < n; j++) {
            tmp[j] = 0;
        }
        numMatrix[i] = tmp;
    }

    // 内存释放
    for (int i = 0; i < n; i++) {
        free(numMatrix[i]);
    }
    free(numMatrix);
}

如图 2-18 所示，该函数的递归深度为 n ，在每个递归函数中都初始化了一个数组，长度分别为 n、n−1、…、2、1 ，平均长度为 n/2 ，因此总体占用 O(n2) 空间：

/* 平方阶（递归实现） */
int quadraticRecur(int n) {
    if (n <= 0)
        return 0;
    int *nums = malloc(sizeof(int) * n);
    printf("递归 n = %d 中的 nums 长度 = %d\r\n", n, n);
    int res = quadraticRecur(n - 1);
    free(nums);
    return res;
}

图 2-18 递归函数产生的平方阶空间复杂度

4. 指数阶 O(2n)

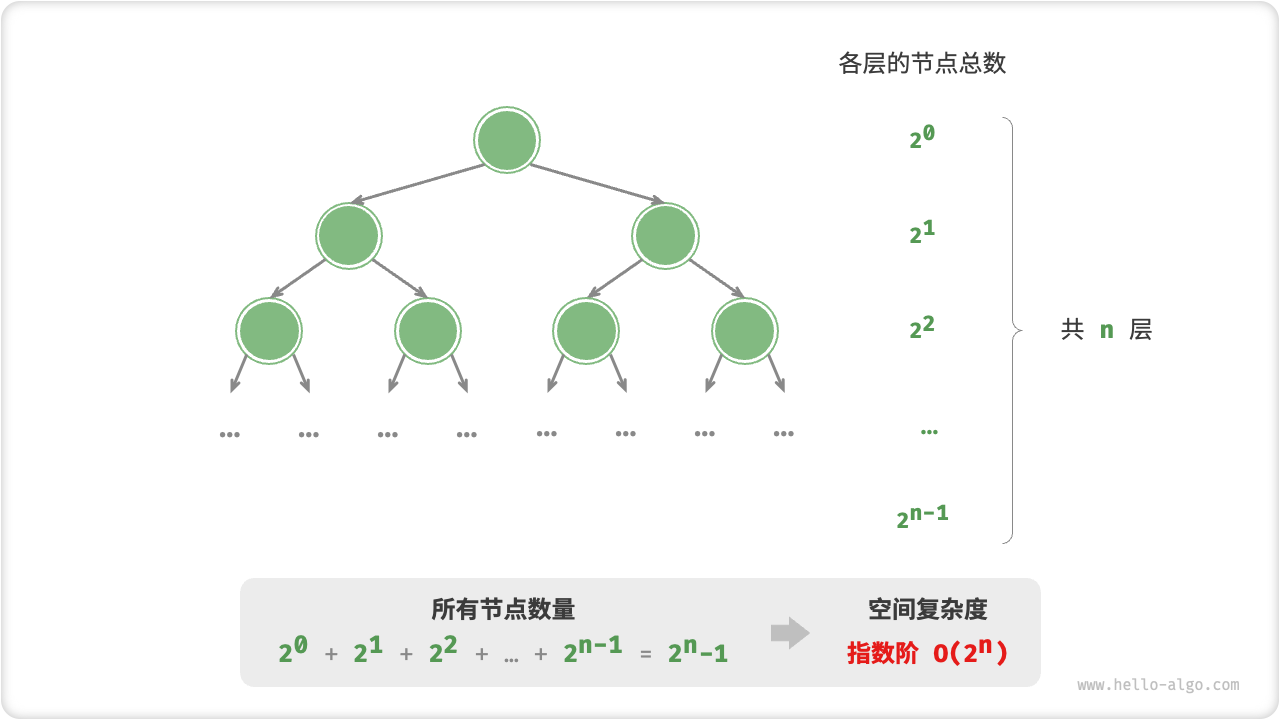
指数阶常见于二叉树。观察图 2-19 ，高度为 n的“满二叉树”的节点数量为 2n−1 ，占用 O(2n) 空间：

/* 指数阶（建立满二叉树） */
TreeNode *buildTree(int n) {
    if (n == 0)
        return NULL;
    TreeNode *root = newTreeNode(0);
    root->left = buildTree(n - 1);
    root->right = buildTree(n - 1);
    return root;
}

图 2-19 满二叉树产生的指数阶空间复杂度

5. 对数阶 O(log⁡n)

对数阶常见于分治算法。例如归并排序，输入长度为 n 的数组，每轮递归将数组从中点划分为两半，形成高度为 log⁡n 的递归树，使用 O(log⁡n) 栈帧空间。

4.4 权衡时间与空间

理想情况下，我们希望算法的时间复杂度和空间复杂度都能达到最优。然而在实际情况中，同时优化时间复杂度和空间复杂度通常是非常困难的。

降低时间复杂度通常需要以提升空间复杂度为代价，反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”；反之，则称为“以时间换空间”。

选择哪种思路取决于我们更看重哪个方面。在大多数情况下，时间比空间更宝贵，因此“以空间换时间”通常是更常用的策略。当然，在数据量很大的情况下，控制空间复杂度也是非常重要的。

5 小结

1. 重点回顾

算法效率评估

时间效率和空间效率是衡量算法优劣的两个主要评价指标。
我们可以通过实际测试来评估算法效率，但难以消除测试环境的影响，且会耗费大量计算资源。
复杂度分析可以克服实际测试的弊端，分析结果适用于所有运行平台，并且能够揭示算法在不同数据规模下的效率。

时间复杂度

时间复杂度用于衡量算法运行时间随数据量增长的趋势，可以有效评估算法效率，但在某些情况下可能失效，如在输入的数据量较小或时间复杂度相同时，无法精确对比算法效率的优劣。
最差时间复杂度使用大 O 符号表示，对应函数渐近上界，反映当 n 趋向正无穷时，操作数量 T(n) 的增长级别。
推算时间复杂度分为两步，首先统计操作数量，然后判断渐近上界。
常见时间复杂度从小到大排列有 O(1)、O(log⁡n)、O(n)、O(nlog⁡n)、O(n2)、O(2n) 和 O(n!) 等。
某些算法的时间复杂度非固定，而是与输入数据的分布有关。时间复杂度分为最差、最佳、平均时间复杂度，最佳时间复杂度几乎不用，因为输入数据一般需要满足严格条件才能达到最佳情况。
平均时间复杂度反映算法在随机数据输入下的运行效率，最接近实际应用中的算法性能。计算平均时间复杂度需要统计输入数据分布以及综合后的数学期望。

空间复杂度

空间复杂度的作用类似于时间复杂度，用于衡量算法占用空间随数据量增长的趋势。
算法运行过程中的相关内存空间可分为输入空间、暂存空间、输出空间。通常情况下，输入空间不计入空间复杂度计算。暂存空间可分为指令空间、数据空间、栈帧空间，其中栈帧空间通常仅在递归函数中影响空间复杂度。
我们通常只关注最差空间复杂度，即统计算法在最差输入数据和最差运行时间点下的空间复杂度。
常见空间复杂度从小到大排列有 O(1)、O(log⁡n)、O(n)、O(n2) 和 O(2n) 等。

2. Q & A

尾递归的空间复杂度是 O(1) 吗？

理论上，尾递归函数的空间复杂度可以被优化至 O(1) 。不过绝大多数编程语言（例如 Java、Python、C++、Go、C# 等）都不支持自动优化尾递归，因此通常认为空间复杂度是 O(n) 。

函数和方法这两个术语的区别是什么？

函数（function）可以被独立执行，所有参数都以显式传递。方法（method）与一个对象关联，被隐式传递给调用它的对象，能够对类的实例中包含的数据进行操作。

下面以几个常见的编程语言来说明。

C 语言是过程式编程语言，没有面向对象的概念，所以只有函数。但我们可以通过创建结构体（struct）来模拟面向对象编程，与结构体相关联的函数就相当于其他语言中的方法。
Java 和 C# 是面向对象的编程语言，代码块（方法）通常都是作为某个类的一部分。静态方法的行为类似于函数，因为它被绑定在类上，不能访问特定的实例变量。
C++ 和 Python 既支持过程式编程（函数），也支持面向对象编程（方法）。

图“常见的空间复杂度类型”反映的是否是占用空间的绝对大小？

不是，该图片展示的是空间复杂度，其反映的是增长趋势，而不是占用空间的绝对大小。

假设取 n=8 ，你可能会发现每条曲线的值与函数对应不上。这是因为每条曲线都包含一个常数项，用于将取值范围压缩到一个视觉舒适的范围内。

在实际中，因为我们通常不知道每个方法的“常数项”复杂度是多少，所以一般无法仅凭复杂度来选择 n=8 之下的最优解法。但对于 n=85 就很好选了，这时增长趋势已经占主导了。