目录
1.1、数据结构的基本概念与学习方法
1.1.1、数据结构的研究对象
(1)、数据结构主要研究的是各种逻辑结构和储存结构以及对数据的各种操作(非数值计算领域的问题)。
(2)、数据结构通常分为三方面:数据的逻辑结构、数据的物理储存结构、对数据的操作(或算法、运算)。
注:①.算法的设计取决于数据的逻辑结构。
②.算法的实现取决于数据的物理存储结构
1.1.2、数据结构的基本概念和基本术语
(1)数据(Data):
数据是所有能被输入到计算机中,且被计算机处理的符号的集合。
(2)数据元素(data element):
数据元素是数据的基本单位,在计算机程序中通常是作为一个整体进行处理和考虑的。
(3)数据项(data item):
数据项是数据结构中讨论的最小单位。
注:①、若数据元素可再分,则每一个独立的处理单元就是数据项。
②、数据元素是数据项的集合。
③、若数据元素不可再分,则数据元素和数据项是同一个概念。、
(4)数据结构(data structure):
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
注:数据结构 = 数据元素+数据元素之间的相互关系 = 对象+关系、
(5)逻辑结构:
逻辑结构是数据之间的相互逻辑关系,他与数据的存储无关。是独立于计算机的。
其中逻辑结构通常分为以下四种结构:
①、线性结构:数据结构中的元素之间存在一对一的相互关系。
关系图如下: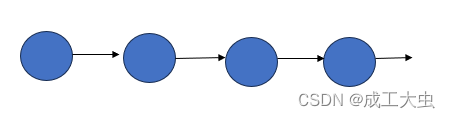
②、树形结构:数据结构中的元素之间存在一对多的相互关系。
关系图如下:

③、图形结构:数据结构中的元素之间存在多对多的相互关系。
关系图如下:
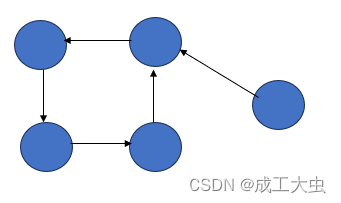
④、集合结构:数据结构的元素之间除了“同属于一个集合”的相互关系外,别无其他关系。
关系图如下:
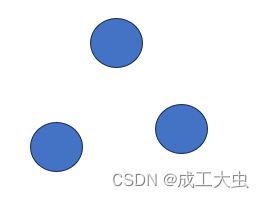
(6)*物理结构(或称存储结构):
物理结构是数据结构在计算机中的表示(又称映像)。
注:物理结构包括数据元素的机内表示和关系的机内表示。
(7)*数据类型:
数据是按数据结构分类的,具有相同数据结构的数据属于同一类,同一类数据的全体称为一个数据类型。
注:
①:在高级程序语言中,数据类型是数据的一种属性,所以数据类型又被认为是一个值的集合和定义在这个值集合上的一组操作的总称。
②:高级语言中的数据类型可以分为两类:原子类型和结构类型。其中原子类型的值是不可分解的,而结构类型的值是由若干成分按某种结构组成的,是可以分解的,并且它的成分既可以是结构化的,也可以是非结构化的。
(8)*抽象数据类型(ADT):
抽象数据类型是指一个数学模型以及定义在此数学模型上的一组操作。
注:抽象的意义在于数据类型的数学抽象特性。数据结构的数据视为抽象数据类型的数据对象,数据结构的关系视为抽象数据类型的数据关系,数据结构上的算法视为抽象数据类型的基本操作。
1.2、算法与数据结构
注:计算机科学家N.Wirth提出一个公式:算法+数据结构=程序
1.2.1、算法的概念
(1)、算法是对特定问题求解步骤的一种描述,它是指令的有限序列,其中每一条指令表示一个或多个操作。
(2)、一个算法必须具备以下5个重要特性:
①、有穷性:一个算法对任何合法的输入值必须总是执行有穷步之后结束,而且每一步都可在有穷时间内完成。
②、确定性:算法中每一条指令必须有确切的含义,阅读时不会产生二义性。
③、可行性:算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
④、输入:一个算法有n(n>=0)个数据的输入
⑤、输出:一个算法必须有一个或多个有效信息的输出,他是与输入有某种特定关系的量。
1.2.2、描述算法的方法
算法可以用自然语言、程序设计语言、类程序设计语言、流程图等来描述。
1.2.3、算法分析
设计算法时,通常应该考虑达到以下目标
①:正确性
②:可读性
③:健壮性
④:高效率:要求执行算法时间短,所需要的存储空间少。
1.2.4、时间复杂度(本章重点):
(1)、一般地,把算法中包含基本操作的执行次数称为算法的时间复杂度。它是一个算法运行时间的相对量度。
(2)、问题的规模是算法求解问题的输入量,一般用整数n表示。
(3)、算法的时间复杂度可看成是问题规模的函数,记为T(n)。
(4)、实际上,一般没有必要精确地计算出算法的时间复杂度,只要大致计算出相应的数量级即可。这种方法称为“大O的渐进表示法”

基本思想:抓大头/取决定性结果的那一项。
例:
1).T(n)=n^2+2n+10 ——> O(n^2) //抓大头
2) .T(n)=2n+10 ——> O(n) //系数需省略
3).T(n)=M+N ——> O(M+N) //M和N的影响性不确定
4).T(n)=3M+2N ——> O(M+N) //M和N的影响性不确定
5).T(n)=M+N ——> O(N) //N的影响远大于M或者N与M的影响持平
6).T(n)=M+N ——> O(M) //M的影响远大于N或者N与M的影响持平
7).T(n)=100 ——> O(1)
8) .T(n)=10000000 ——> O(1)
注:O(1)不是一次,而是代表常数次
(5)、有多种情况的算法的时间复杂度,即存在最好的情况、最坏的情况、平均情况,此时已最坏的情况的时间复杂度为主。

例:
1).冒泡排序算法的时间复杂度(O(n^2))
①:最好的情况:数组已经有序,只需遍历一次数组 ——> O(n)
②:最坏的情况:数组逆序的情况,次数为(n-1)+(n-2)+......+2+1,即(n*(n-1))/2 ——> O(n^2)
2) .二分查找算法的时间复杂度(O())
①:最好的情况:第一次就找到 ——> O(1)
②:最坏的情况:查找区间缩放只剩下一个值时(找到最后一个值的情况)。
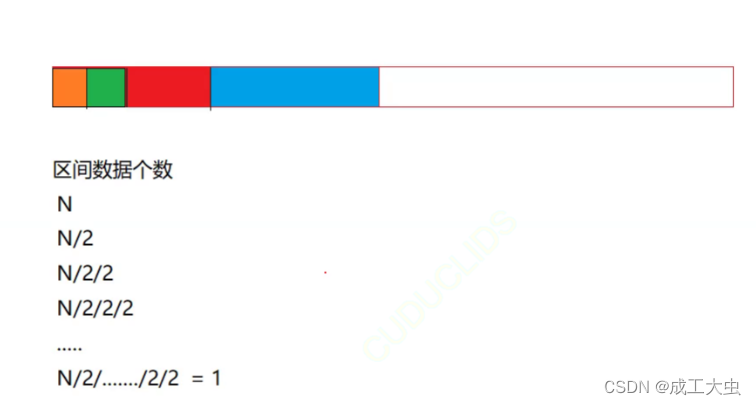
由图可知,除了多少次2就代表找了多少次
假设找了x次,则有:
2^x=N
所以:
x==T(n)
即时间复杂度为 O()或者O(
)
注:对数在文本中不方便书写,只要在一些支持公式展示的编辑器才方便书写,所以若对数是以2为底的时候可以省略2,如下:
O() ~ O(
)
3) .如图(O(2^N))

遇到递归,小编认为画图更有助于我们理解:
该函数可抽象化为如下图右下角被砍掉的三角形

当一步一步进入递归,我们会发现每次进行递归的次数有如下规律:
所以基本操作次数可近似等于:(2^0)+(2^1)+(2^2)+......+(2^N-1),进行求和即(2^N)-1
所以时间复杂度为:O(2^N)
(6)、性能比较:O(1)<O(log n)<O(n)<O(nlog n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
经典例题——消失的数字

该题小编一共提供三种思路:
(1).先将数组排序在进行遍历,时间复杂度为:O(logn*n)
(2).将0到n的等差数列求和再减去数组中的数,结果就等于消失的数字,时间复杂度为:O(n)

(3).“单身狗思路”: 异或(^)
几个常用公式:
①:a^b ^b=a
②:a^b ^a=b
③:a^b^a^b=a^a^b^b(交换律)
这里我们假设消失的数为x,并设为上式中的a (即数x)
0到n的等差数列中除去数x的剩余数组为上式中的b(即数组nums)
所以a^b即为,0到n的等差数列中所有数异或在一起:(1^2^3^4^...^x^...^n)
所以根据公式a^b^b =a,可知
1^2^3^...^x^...^n-1^n^(nums)=消失的数x
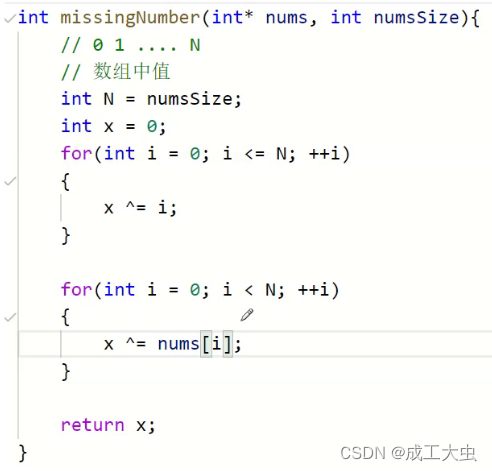
所以如代码所示,T(n)=2n+1
所以时间复杂度为:O(n)
1.2.5、空间复杂度
(1)、空间复杂度相关介绍如下图:
 初学者只讲概念肯定看的很懵,下面用几个例子来帮助我们理解:
初学者只讲概念肯定看的很懵,下面用几个例子来帮助我们理解:
例:
1).如下图中,一般情况形参与空间复杂度无关,所以数组a和整形n不算空间复杂度,空间复杂度是在实现冒泡排序算法的时候所临时开辟的空间,如下图所临时开辟的空间有end、exchange、i,所以T(n)=3,空间复杂度为O(1)
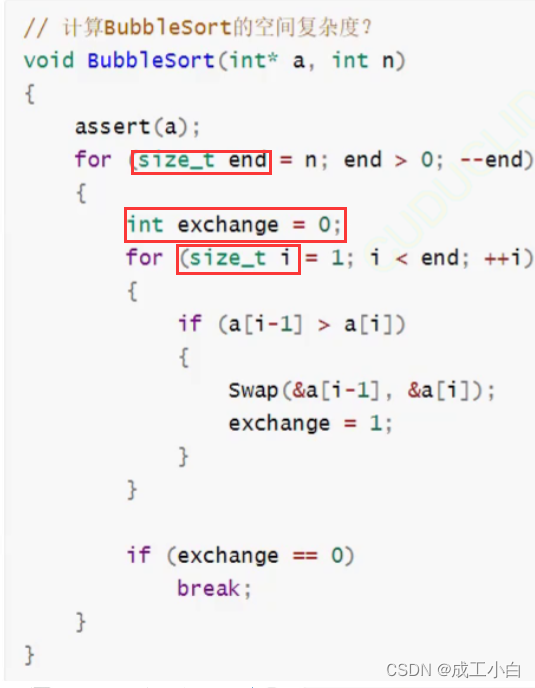
2).计算斐波那契数列的空间复杂度

我们能注意到,该算法临时开辟的空间有以上红色方框,所以T(n)=n+2,空间复杂度为O(n)。
注:空间复杂度比时间复杂度简单,大多数都是O(n)或O(1)
3).下面来看关于递归的空间复杂度:

前面谈到遇到递归,习惯画图理解

由上,一般递归也属于一种算法,那么N以后的递归中,栈帧开辟的空间也算临时开辟空间,每个栈帧开辟常数次空间(O(1)),N个栈帧就开辟n次空间,所以该算法的空间复杂度为O(n)。(该解释可能有些知识点误差,仅供参考和提供思路)。
4).计算斐波那契数递归的空间复杂度:

同理,递归我们画出内部图:
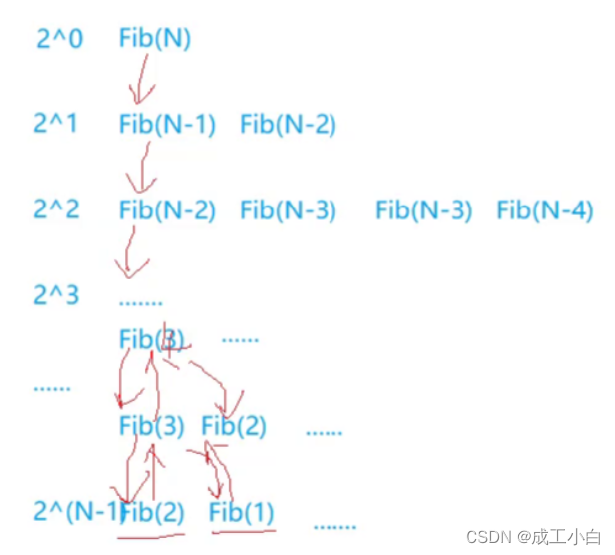
如图计算斐波那契递归的空间复杂度,在上面我们谈到该算法时间复杂度为O(2^n),初学空间复杂度的时候,理解不深刻,很容易以为该算法空间复杂度和时间复杂度一样,但实则不然,这里我们要记住一句很关键的话话:
时间是累积的,一去不复返
空间是可重复利用的。
所以由上图所见,第一层Fib(N-1)递归下去,栈帧总的会开辟n个空间,第一轮递归结束后,所用空间又会还给操作系统,然后当进行加法的右边Fib(N-2)的递归时,会重复使用第一轮递归所用的空间,所以总的空间开辟了n个,所以空间复杂度为O(n)
(该解释可能有部分知识误差,仅供参考和提供思路)
这里解释起来可能有点抽象,下面举个例子可以帮助我们理解:
如下面一段代码:
void fun1()
{
int a = 0;
printf("%p\n", &a);
}
void fun2()
{
int b = 0;
printf("%p\n", &b);
}
int main()
{
fun1();
fun2();
return 0;
}运行结果如下图:
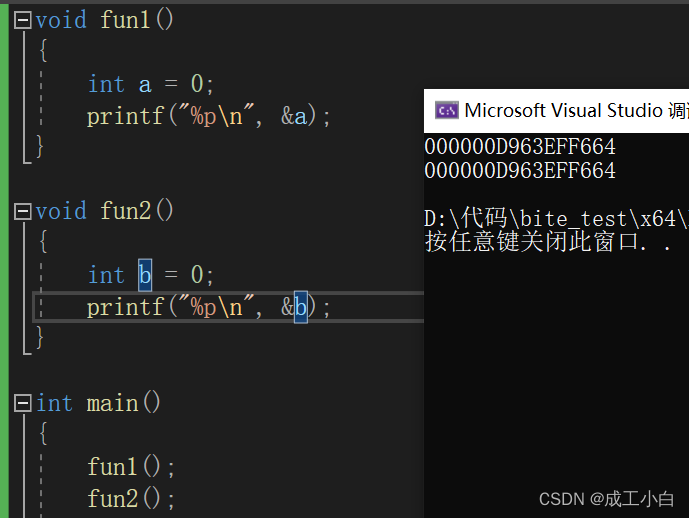
在 main函数里依次调用函数fun1和fun2,会发现在两个函数里面创建的变量所占的是同一份空间,这就是因为在fun1函数调用结束后,其栈帧会销毁,所用空间会还给操作系统,当调用fun2,时就可以使用fun1函数里的变量所使用的空间(注意,函数的地址和栈帧开辟空间没有关系,两个函数的地址不一样,但所创建的变量所用空间是一样的,在这里小编建议大家学习一下函数栈帧的创建和销毁,理解起来更容易)。
(2)、以上几种事例基本上包括了基础的百分之90的空间复杂度算法,到后面在慢慢深度剖析。
经典例题——轮转数组


这道题最佳解法为:
时间复杂度为O(n)
空间复杂度为O(1)
小编在此提供三种解法:
注:在理解题意之后,我们会发现当k(旋转个数)等于元素总数时会还原数组,所以不管三七二十一,每种算法上来就将k%=n(n为数组元素个数),以便去掉重复旋转的情况。
①:创建一个变量,每次将数组nums的最后一个数记录下来,在将前n-1个(n为数组元素个数)数依次向后移动,再把所记录的数放在nums[0]处,如此循环k次即可:

该算法:
时间复杂度O(n^2):因为最坏的情况时,k==n,这时需要移动数组前n-1个数共(n*n)次。
空间复杂度O(1):因为只创建了一个临时变量用于记录数组nums最后一个值。
②:用空间换时间的方式,动态分配一个临时数组tmp,先将数组nums的后k个数粘贴到该临时数组里面,再将数组num前n-k个数粘贴到临时数组里面,最后在将临时数组整体粘贴到数组nums(习惯用函数memcpy用于两个数组之间进行粘贴,不同小伙伴可以学习一下。)
时间复杂度:O(n):因为后面要将临时数组tmp的值一个个赋值给nums
空间复杂度:O(n):因为动态开辟了一个大小为(n*sizeof(int))字节的数组(与nums等大)
代码实现如下:
#include<string.h>
void rotate(int* nums, int n, int k)
{
k %= n;
int* tmp = (int*)malloc(sizeof(int) * n);
memcpy(tmp, nums + n - k, sizeof(int) * k);
memcpy(tmp + k, nums, sizeof(int) * (n - k));
memcpy(nums, tmp, sizeof(int) * n);
free(tmp);
tmp = NULL;
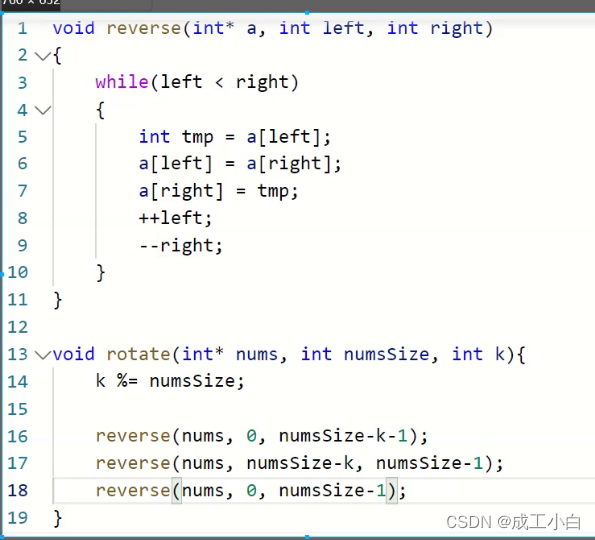
}③:这种方法即为最佳方法:即旋转三次,如下:

时间复杂度:O(n):
空间复杂度:O(1):
代码实现如下:
本章知识到此为止,希望对你有所帮助!