语言模型Performer:一种基于Transformer架构的通用注意力框架
Performer是一种用于高效处理自注意力机制(Self-Attention)的神经网络架构。自注意力机制在许多自然语言处理和计算机视觉任务中取得了出色的成绩,但由于其计算复杂度与序列长度的平方成正比,因此在处理长序列时存在问题。为了解决这些问题,Google AI引入了Performer,这是一种 具有线性扩展性的Transformer架构,其注意机制具有线性扩展性。该框架是通过
Fast Attention Via Positive Orthogonal Random Features(
FAVOR+)算法实现的,该算法提供了可扩展的、低方差和无偏估计,可以表达由随机特征图分解(特别是常规softmax-attention)表示的注意机制。这种映射有助于保持线性的空间和时间复杂度。
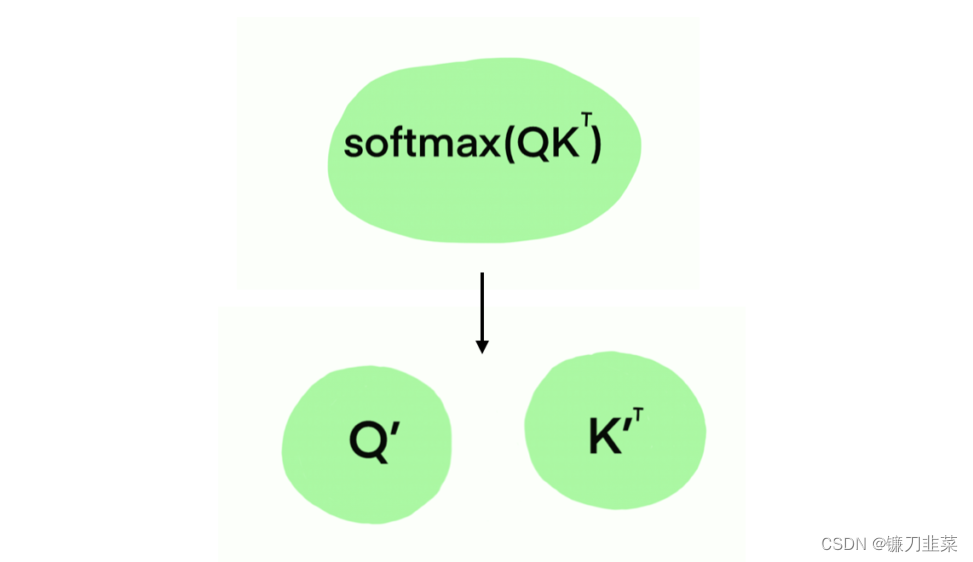
Performer的核心思想是采用低秩近似来替代传统的完全连接的自注意力矩阵,从而减少计算复杂度。具体来说,Performer使用了以下几种关键技巧:
- Fast Attention: 在传统的自注意力机制中,需要计算所有位置之间的注意力权重,这会导致计算复杂度为 O ( n 2 ) O(n^2) O(n2),其中 n n n是序列长度。Performer通过引入可固定的随机投影矩阵,将这一计算复杂度降低到了 O ( n ) O(n) O(n)。这个技巧使得自注意力计算的时间复杂度与序列长度线性相关,而不是二次相关。
- Orthogonal Random Features: Performer使用正交随机特征,这些特征可以在保持模型性能的同时进一步提高计算效率。这些特征可以使得投影矩阵的计算更加高效。
- Memory Efficient: Performer还提出了一种内存高效的变种,可以处理长序列而不会受到内存限制的限制。这个方法通过分块计算自注意力矩阵来实现。
- Favorable Asymptotics: 与标准自注意力相比,Performer在序列长度增加时具有更好的渐进计算复杂度,这意味着它在处理长序列时具有明显的优势。
总的来说,Performer算法通过引入随机特征和低秩近似,以及一些其他技巧,显著提高了自注意力模型的计算效率,使得它们可以应用于更长的序列,同时不牺牲模型性能。这使得它在自然语言处理和其他领域的应用中具有广泛的潜力。
Performer论文解读

论文摘要:我们引入了Performer,这是一种Transformer架构,可以准确估计常规(softmax)全秩注意力的Transformer,但只使用线性空间和时间复杂度(而不是二次复杂度),而且不依赖于任何先验条件,如稀疏性或低秩性。为了近似softmax注意力核,Performers使用一种新颖的Fast Attention Via positive Orthogonal Random features方法(FAVOR+),这对于可扩展的核方法可能具有独立的兴趣。FAVOR+还可用于高效地建模softmax以外的可核化注意机制。这种表示能力对于首次在大规模任务上准确比较softmax与其他核函数至关重要,这是常规Transformer所无法达到的,还可以研究最优的注意力核函数。Performers是线性架构,与常规的Transformer完全兼容,并具有强大的理论保证:对注意力矩阵的无偏或几乎无偏估计、均匀收敛和低估计方差。我们在一系列丰富的任务上测试了Performers,从像素预测到文本模型再到蛋白质序列建模,都取得了竞争力强的结果,超越了其他经过检验的高效稀疏和密集注意方法,展示了Performers所利用的新型注意力学习范式的有效性。
用人话说:Performer是一个Transformer架构,其注意力机制可线性扩展,一方面可以让模型训练得更快,另一方面也能够让模型处理更长的输入序列。这对于某些图像数据集(如ImageNet64)和文本数据集(如PG-19)来说定然是很香的。Performer使用了一个高效的(线性)通用注意力框架,在框架中使用不同的相似度测量(即各种核方法)可以实现各种注意力机制。该框架由FAVOR+(Fast Attention Via Positive Orthogonal Random Features,通过正交随机特征实现快速注意力)算法实现,该算法提供了可扩展、低方差、无偏估计的注意力机制,可以通过随机特征图分解来表达。该方法一方面确保了线性空间和时间复杂度,另一方面也保障了准确率。此外,该方法可以单独用于softmax 运算,还可以和可逆层等其他技术进行配合使用。
针对那些需要长距离注意力的应用,部分研究者已经提出了一些速度快、空间利用率高的方法,其中比较普遍的方法是稀疏注意力。

图. 标准的稀疏化技术
然而,稀疏注意力方法也有一些局限。首先,它们需要高效的稀疏矩阵乘法运算,但这并不是所有加速器都能做到的;其次,它们通常不能为自己的表示能力提供严格的理论保证;再者,它们主要针对 Transformer 模型和生成预训练进行优化;最后,它们通常会堆更多的注意力层来补偿稀疏表示,这使其很难与其他预训练好的模型一起使用,需要重新训练,消耗大量能源。
此外,稀疏注意力机制通常不足以解决常规注意力方法应用时所面临的所有问题,如指针网络。还有一些运算是无法稀疏化的,比如常用的 softmax 运算。
Regular Attention Mechanism
常规的注意力机制中,对应矩阵行与列的 Query 和 Key 相乘,再通过 Softmax 计算出注意力得分矩阵。公式如下:
Attention ( Q , K , V ) = softmax ( Q K T d ) V \text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d}})V Attention(Q,K,V)=softmax(dQKT)V
其中 Q , K , V Q, K, V Q,K,V(维度是 L × d L \times d L×d)分别是queries、keys和values矩阵。 L L L是句子的长度, d d d是queries,keys和values向量的(任意)维度。Transformer的问题来自softmax函数,让我们看看原因。
这种方法不能将query-key传递到非线性 softmax 操作之后的结果分解回原来的key和query,但是可以将注意力矩阵分解为原始query和key的随机非线性函数的乘积,也就是所谓的随机特征(random features),这样就可以更有效地对相似性信息进行编码。
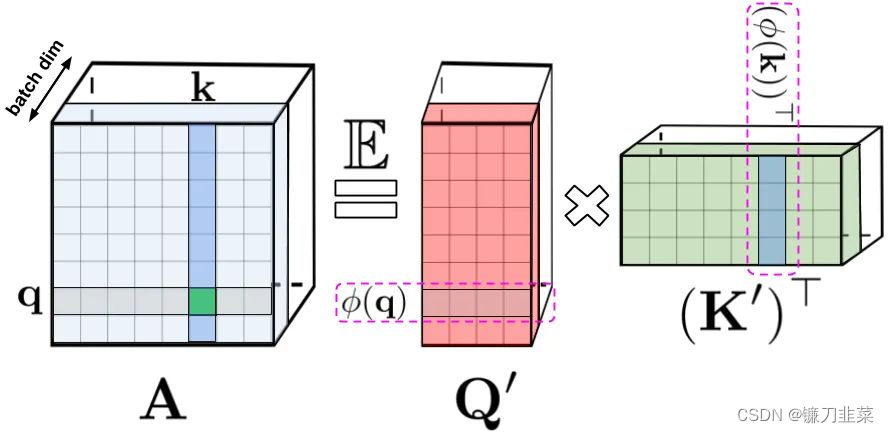
标准注意力矩阵包括每一对 entry 的相似度系数,由 query 和 key 上的 softmax 计算组成,表示为 q 和 k。
常规的 softmax 注意力可以看作是由指数函数和高斯投影定义的非线性函数的一个特例。在这里我们 也可以反向推理,首先实现一些更广义的非线性函数,隐式定义 query-key 结果中其他类型的相似性度量或核函数。研究者基于早期的核方法(kernel method),将其定义为通用注意力(generalized attention)。尽管对于大多核函数来说,闭式解并不存在,但这一机制仍然可以应用,因为它并不依赖于闭式解。
文章首次证明了,在下游 Transformer 的应用中,任意注意力矩阵都可以通过随机特征实现有效近似。实现这一点的新机制使用positive random features(正向随机特征),即原始 query 和 key 的正值非线性函数。这避免了训练过程中的不稳定,并实现了对常规 softmax 注意力的更准确近似。
FAVOR+:通过矩阵相关性实现快速注意力
通过上述的分解可以得到线性(而非二次)空间复杂度隐式注意力矩阵。同样,通过分解可以获得线性时间的注意力机制。原有的方式是注意力矩阵与value输入相乘得到最终结果,但在分解注意力矩阵之后,可以重新排列矩阵乘法来近似常规注意力机制的结果,而无需显式地构建二次方大小的注意力矩阵。最终生成了新算法 FAVOR+。
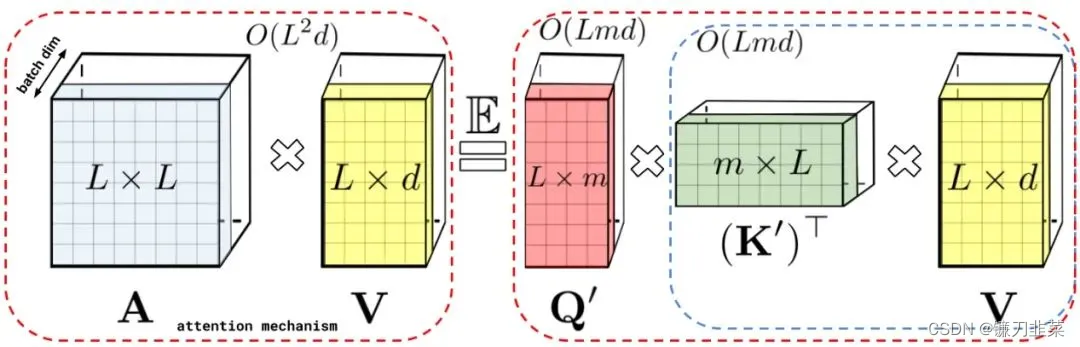
图:通过(随机)特征图近似regular attention mechanism AV(在 D − 1 D^{−1} D−1归一化之前)。虚线块表示计算顺序,并附有相应的时间复杂度。左:标准注意力模块计算,其中通过执行带有矩阵 A 和值张量 V 的矩阵乘法来计算最终的预期结果;右:通过解耦低秩分解 A 中使用的矩阵 Q ′ Q′ Q′ 和 K ′ K′ K′ 以及按照虚线框中指示的顺序执行矩阵乘法,研究者获得了一个线性注意力矩阵,同时不用显式地构建 A A A 或其近似。
上述分析与双向注意力(即非因果注意力)相关,并没有区分 past 和 future的部分。那么如何做到让输入序列中只注意到其中一部分,即单向的因果注意力?只需使用前缀和计算(prefix-sum computation),在计算过程只存储矩阵计算的运行总数,而不存储完整的下三角regular attention矩阵。
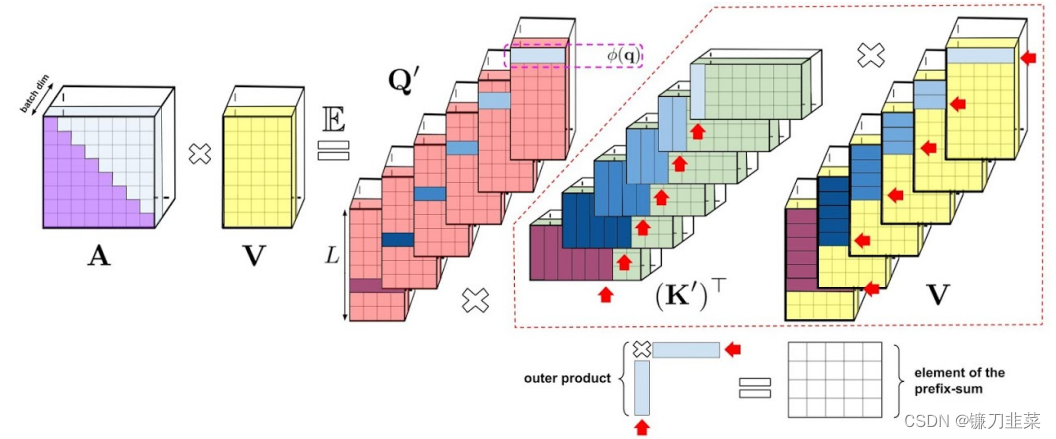
图:展示了单向注意力的前缀和算法(prefix-sum algorithm)的可视化表示。为了清晰起见,我们在此可视化中省略了注意力归一化。该算法保留前缀和,前缀和是通过将与keys对应的随机特征与values向量的外积相加而获得的矩阵。在前缀和算法的每个给定迭代中,与query 对应的随机特征向量与最近的前缀和(通过对应于之前tokens 的所有外积相加而得到)相乘,从而得到由注意力机制输出的矩阵 A V AV AV的新行(new row)。也就是说,key向量和value向量的随机特征映射进行外积,得到的前缀和,且这个过程是动态构建的。最后将随机特征向量与query左乘得到最终矩阵中的新行。其中左边 A A A表示标准单向注意力需要 mask 注意力矩阵以获得其下三角部分。
Attention的时间复杂性
回顾一下,维度分别为 n × m n\times m n×m和 m × p m\times p m×p的两个矩阵相乘的时间复杂度为 O ( n m p ) O(nmp) O(nmp)。如果我们看一下注意力方程,我们会发现我们正在乘以三个矩阵: Q Q Q(维度为 L × d L\times d L×d), K T K^T KT(维度为 d × L d\times L d×L)和 V V V(维度为 L × d L\times d L×d)。我们将获得不同的复杂性,这取决于我们将它们相乘的顺序。先忽略softmax和分母 d \sqrt{d} d(这只是一个标量),我们可以看到:首先通过 Q K T QK^T QKT的乘积,得到了 O ( L 2 d ) O(L^2d) O(L2d)的复杂度,如果令 K T V K^TV KTV首先相乘,我们得到一个 O ( d 2 L ) O(d^2L) O(d2L)的复杂度。
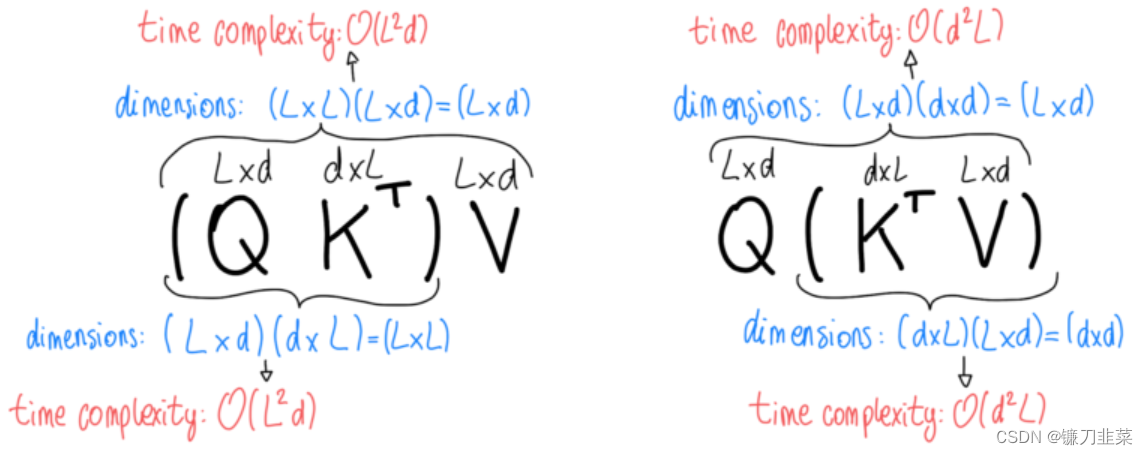
显然,我们应该选择 O ( d 2 L ) O(d^2L) O(d2L),因为 d d d是一个我们可以选择的参数,而且我们可以有 d < L d<L d<L。然而,我们实际上不能按这个顺序进行乘法运算,因为 Q K T QK^T QKT“卡”在softmax内部,没有简单的方法将其取出。这意味着我们不得不处理 O ( L 2 d ) O(L^2d) O(L2d)的时间复杂性,其在序列长度上是二次的(因此处理较长的序列在计算上变得越来越昂贵)。因此,softmax是transformers的瓶颈,我们想找到一种方法来解决这个问题。
绕过softmax瓶颈
从高层次上讲,本文提出的方法非常简单。我们能否找到一种方法来近似softmax,使我们能够选择矩阵的计算顺序?本质上,我们要找到一些矩阵 Q ′ Q' Q′和 K ′ K' K′,满足 Q ′ K ′ ≈ softmax ( Q K T / d ) Q'K'\approx \text{softmax}(QK^T/\sqrt{d}) Q′K′≈softmax(QKT/d)目标很简单,但如何实现目标的细节有点复杂。
首先,让我们回忆一下,softmax是一个函数,给定长度为 n n n 的向量 z \mathbf{z} z,将所有元素 z i \mathbf{z}_i zi归一化为: σ ( z ) i = e z i ∑ j = 1 n e z j \sigma (\mathbf{z} )_i=\frac{e^{z_i}}{\sum j=\mathbf{1}^ne^{z_j} } σ(z)i=∑j=1nezjezi鉴于此,请注意,我们可以将注意力方程中的softmax重写为: softmax ( Q K T d ) = D − 1 A \text{softmax}(\frac{QK^T}{\sqrt{d}})=D^{-1}A softmax(dQKT)=D−1A其中 A = e x p ( Q K T / d ) A=exp(QK^T/\sqrt{d}) A=exp(QKT/d), D = diag ( A 1 L ) D=\text{diag}(A\mathbf{1}_L) D=diag(A1L),diag是将一个输入向量变为对角矩阵, 1 L \mathbf{1}_L 1L则是一个长度为 L L L的全为1的向量。即文中的公式(1):
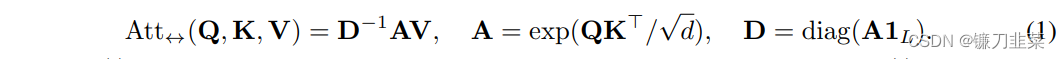
where the exponential in A A A is applied element-wise, D D D is the diagonal matrix with elements A 1 L A\mathbf{1}_L A1L。 diag ( A 1 L ) \text{diag}(A\mathbf{1}_L) diag(A1L)是为了求和, D − 1 D^{-1} D−1则是将这些和变成倒数,所以 D − 1 A D^{-1}A D−1A跟 softmax ( Q K T / d k ) \text{softmax}(QK^T/\sqrt{d_k}) softmax(QKT/dk)是等价的。事实上, A 1 L A\mathbf{1}_L A1L只是一个长度为 L L L的向量,它是通过对 A A A的列求和而得到的。
注意: A A A的element-wise exponential是这里的真正问题,所以我们的目标是以某种方式分解它。我们可以忽略标量分母 d \sqrt{d} d因为它只是用于归一化,但是我们可以等价地normalize queries和keys。这意味着我们的目标是找到一些 Q ′ Q' Q′和 K ′ K' K′,满足: Q ′ K ′ ≈ exp ( Q K T ) Q'K'\approx \text{exp}(QK^T) Q′K′≈exp(QKT)
通过Gaussian kernel求Softmax kernel
在上面的公式中, A A A是两个矩阵的乘积除以常数后再做一个指数操作,得到一个注意力矩阵,在这里,引入核方法来对这个注意力矩阵A做近似。这就是核方法发挥作用的地方。
具体的方法如下:
我们知道kernels是等价于某个特征图(feature map) φ \varphi φ的点积的functions。对于 Q Q Q和 K K K中的任何一个向量 q i q_i qi和 k j k_j kj,它们原来的相似度不考虑归一化的结果是 e x p ( q i k j ) exp(q_ik_j) exp(qikj)。在引入核方法后,计算方式变为: K ( x , y ) = E [ ϕ ( x ) T , ϕ ( y ) T ] K(x, y)=\mathbb{E}[\phi(x)^T, \phi(y)^T] K(x,y)=E[ϕ(x)T,ϕ(y)T]通常,给定某个高维特征图 φ \varphi φ,我们有兴趣的是找到一个等价函数 K K K,这将使我们避免在 φ \varphi φ的高维空间中进行计算。然而,在我们的情况下,我们实际上会走相反的路:如果我们假设 A A A是一个包含元素 A ( i , j ) = K ( q i , k j ) = e x p ( q i k j T ) A(i,j)=K(q_i,k_j)=exp(q_ik_j^T) A(i,j)=K(qi,kj)=exp(qikjT)(其中 q i q_i qi和 k j k_j kj分别是 Q Q Q和 K K K的行向量)的核矩阵,我们能找到一个特征图 φ \varphi φ来帮助我们分解 A A A吗? A ( i , j ) = K ( q i , k j ) = exp ( q j k j T ) = ϕ ( q i ) T ϕ ( k j ) \mathbf{A}(i,j)=K(q_i,k_j)=\text{exp}(q_jk_j^T)=\phi(q_i)^T\phi(k_j) A(i,j)=K(qi,kj)=exp(qjkjT)=ϕ(qi)Tϕ(kj)
现在,大多数kernels可以通过以下形式的特征图 φ \varphi φ来近似:

其中 h h h和 f 1 , . . . , f l f_1, ..., f_l f1,...,fl是不同的确定性映射函数, w 1 , . . . , w m w_1, ..., w_m w1,...,wm则是从一个分布 D D D中采样出来的,即它们是独立同分布的。因此 φ ( x ) \varphi(x) φ(x)是一个有 l × m l\times m l×m个元素的向量。
- 当 h ( x ) = 1 h(x)=1 h(x)=1, l = 1 l=1 l=1, D = N ( 0 , I d ) D=N(0, I_d) D=N(0,Id)的时候,这个核就是所谓的
PNG-kernel。 - 当 h ( x ) = 1 h(x)=1 h(x)=1, l = 2 l=2 l=2, f 1 = s i n f_1=sin f1=sin, f 2 = c o s f_2=cos f2=cos的时候,就是
shift-invariant核。此时如果 D = N ( 0 , I d ) D=N(0, \mathbf{I}_d) D=N(0,Id),那么就是高斯核。
也就是说,如果我们从具有均值 0 和单位方差的正态分布中绘制 w ,我们可以通过使用特征图来获得高斯核:
ϕ ( x ) g a u s s = 1 m ( sin ( w 1 T x ) , . . . , sin ( w m T x ) , cos ( w 1 T x ) , . . . , cos ( w m T x ) ) \phi(\mathbf{x})_{gauss}=\frac{1}{\sqrt{m}}(\text{sin}(w_1^T\mathbf{x}),...,\text{sin}(w_m^T\mathbf{x}),\text{cos}(w_1^T\mathbf{x}),...,\text{cos}(w_m^T\mathbf{x})) ϕ(x)gauss=m1(sin(w1Tx),...,sin(wmTx),cos(w1Tx),...,cos(wmTx))注意,具有单位方差的高斯核由下式给出:
K g a u s s = exp ( − ∣ ∣ x − y ∣ ∣ 2 2 ) \mathbf{K}_{gauss}=\text{exp}(-\frac{||\mathbf{x}-\mathbf{y}||^2}{2} ) Kgauss=exp(−2∣∣x−y∣∣2)现在请记住,我们想要找到一个softmax内核:
K S M ( x , y ) = exp ( x T y ) \mathbf{K}_{SM}(\mathbf{x},\mathbf{y})=\text{exp}(\mathbf{x}^T\mathbf{y}) KSM(x,y)=exp(xTy)我们可以看到,Softmax核的结构与高斯核并不相距太远。事实证明,我们可以利用这种相似性来找到softmax内核。事实上,请注意
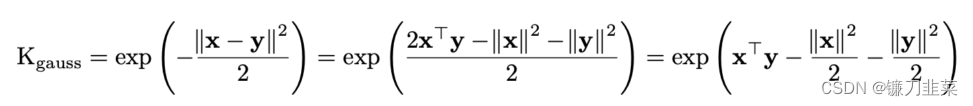
这意味着我们实际上可以将softmax内核重写为:
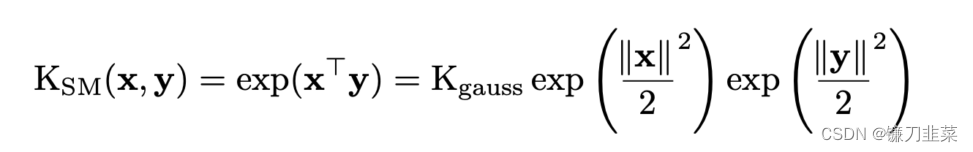
并且,我们可以通过将 h h h 函数从 h ( x ) = 1 h(x)=1 h(x)=1改变为如下形式,重用导致高斯核的特征映射。
h ( x ) = exp ( ∣ ∣ x ∣ ∣ 2 2 ) h(x)=\text{exp}(\frac{||x||^2}{2}) h(x)=exp(2∣∣x∣∣2)
这是一个不错的近似值,但也有一些问题。softmax函数总是输出正值,因此 A \mathbf{A} A的所有元素都应该是正值。然而,使用这个内核来近似softmax可能会给出一些负值。事实上,由于我们从均值为 0 的正态分布中绘制 w ,其中一些值将为负,这反过来意味着 A \mathbf{A} A的一些值将是负的。这会导致问题和异常行为。
寻找更稳定的Softmax内核
研究人员发现softmax内核也可以重写为:
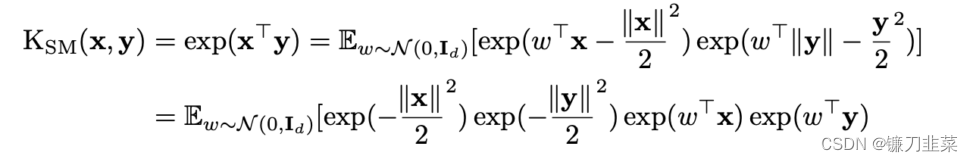
(这实际上是softmax内核的证据可以在论文的附录中找到。)因此,我们可以简单地采用之前的特征图形式并设置 h ( x ) = exp ( − ∣ ∣ x ∣ ∣ 2 2 ) , l = 1 , f 1 = exp , D = N ( 0 , I d ) h(\mathbf{x})=\text{exp}(-\frac{||x||^2}{2}),l=1,f_1=\text{exp},\mathcal{D}=\mathcal{N}(0,\mathbf{I}_d) h(x)=exp(−2∣∣x∣∣2),l=1,f1=exp,D=N(0,Id)以得到 ϕ ( x ) S M = 1 m exp ( − ∣ ∣ x ∣ ∣ 2 2 ) ( exp ( w 1 T x ) , . . . , exp ( w m T x ) ) \phi(\mathbf{x})_{SM}=\frac{1}{\sqrt{m}}\text{exp}(-\frac{||\mathbf{x}||^2}{2})(\text{exp}(w_1^T\mathbf{x}),...,\text{exp}(w_m^T\mathbf{x})) ϕ(x)SM=m1exp(−2∣∣x∣∣2)(exp(w1Tx),...,exp(wmTx))
通过这样做,我们可以看到所有的值都是正的,因为我们使用的是 exp \text{exp} exp,因此解决了以前的问题。作者还提出了一个替代的特征图,可以导致相同的内核,如果感兴趣,可以阅读原始论文。
论文中对上述内容的描述:

使用Softmax核函数查找Q’和V’
回顾一下。我们从注意力方程式开始 Attention ( Q , K , V ) = softmax ( Q K T d ) V \text{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\text{softmax}(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}})\mathbf{V} Attention(Q,K,V)=softmax(dQKT)V发现我们可以将其重写为:
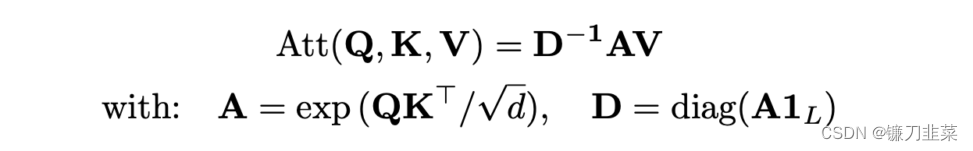 然后,我们找到了Softmax kernel的特征图,可以用来近似矩阵 A \mathbf{A} A:
然后,我们找到了Softmax kernel的特征图,可以用来近似矩阵 A \mathbf{A} A:
ϕ ( x ) S M = 1 m exp ( − ∣ ∣ x ∣ ∣ 2 2 ) ( exp ( w 1 T x ) , . . . , exp ( w m T x ) ) \phi(\mathbf{x})_{SM}=\frac{1}{\sqrt{m}}\text{exp}(-\frac{||\mathbf{x}||^2}{2})(\text{exp}(w_1^T\mathbf{x}),...,\text{exp}(w_m^T\mathbf{x})) ϕ(x)SM=m1exp(−2∣∣x∣∣2)(exp(w1Tx),...,exp(wmTx))
因此,我们现在可以使用特征图(feature map)替换 A \mathbf{A} A中的元素:
A ( i , j ) = K ( q i , k j ) = exp ( q i k j T ) = ϕ S M ( q i T ) ϕ S M ( k j ) \mathbf{A}(i,j)=\mathbf{K}(\mathbf{q}_i,\mathbf{k}_j)=\text{exp}(\mathbf{q}_i\mathbf{k}_j^T)=\phi_{SM}(\mathbf{q}_i^T)\phi_{SM}(\mathbf{k}_j) A(i,j)=K(qi,kj)=exp(qikjT)=ϕSM(qiT)ϕSM(kj)
注意,我们从长度为 L L L的向量 q i \mathbf{q}_i qi, k j \mathbf{k}_j kj移动到长度为 m m m的向量 ϕ S M ( q i ) \phi_{SM}(\mathbf{q}_i) ϕSM(qi), ϕ S M ( k j ) \phi_{SM}(\mathbf{k}_j) ϕSM(kj)。
我们现在可以将 A \mathbf{A} A分解为 Q ′ Q' Q′和 K ′ K' K′,其中 Q ′ Q' Q′和 K ′ K' K′的元素是 ϕ S M ( q i ) \phi_{SM}(\mathbf{q}_i) ϕSM(qi)和 ϕ S M ( k j ) \phi_{SM}(\mathbf{k}_j) ϕSM(kj)。
最后,我们可以自由地改变矩阵乘法的顺序,并将时间复杂度从 O ( L 2 d ) O(L^2d) O(L2d)降低到 O ( L m d ) O(Lmd) O(Lmd),从而在序列长度上获得线性而不是二次(quadratic)的复杂度。
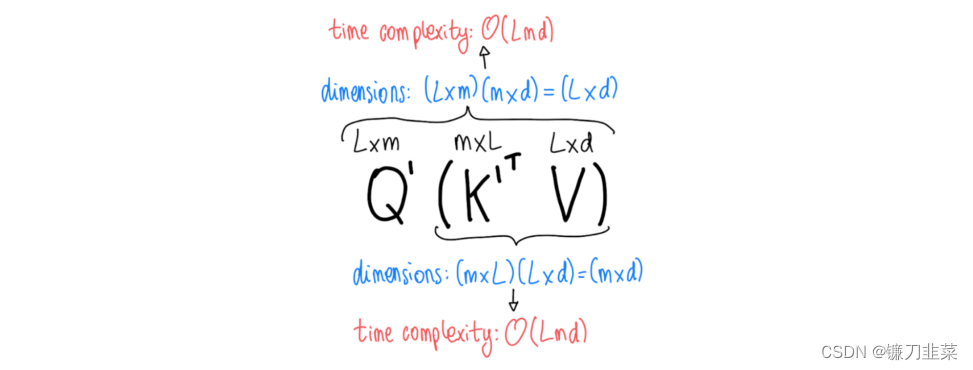
总结
本质上,在本文中,作者设法找到了一种使用特征图的点积来近似softmax函数的方法。正因为如此,transformers中计算注意力的时间复杂度可以从序列长度的quadratic降低到linear,也就是将指数操作进行拆分近似。当处理长序列时,这将大大加快transformers的速度。同时,在保证近似的程度上,使用了核方法,正值和正交等技巧。
另外,需要注意的是:
- 虽然这种方法是在考虑transformers的情况下开发的,但它实际上可以应用于任何需要softmax的模型。
- 作者指出,这种方法不仅速度更快,而且内存效率更高。这可以通过查看需要存储的矩阵的维度来看出。
代码可用性
一种Performer的PyTorch实现:https://libraries.io/pypi/performer-pytorch,安装方式如下:
pip install performer-pytorch==1.1.4
使用示例:
import torch
from performer_pytorch import PerformerLM
model = PerformerLM(
num_tokens = 20000,
max_seq_len = 2048, # max sequence length
dim = 512, # dimension
depth = 12, # layers
heads = 8, # heads
causal = False, # auto-regressive or not
nb_features = 256, # number of random features, if not set, will default to (d * log(d)), where d is the dimension of each head
feature_redraw_interval = 1000, # how frequently to redraw the projection matrix, the more frequent, the slower the training
generalized_attention = False, # defaults to softmax approximation, but can be set to True for generalized attention
kernel_fn = torch.nn.ReLU(), # the kernel function to be used, if generalized attention is turned on, defaults to Relu
reversible = True, # reversible layers, from Reformer paper
ff_chunks = 10, # chunk feedforward layer, from Reformer paper
use_scalenorm = False, # use scale norm, from 'Transformers without Tears' paper
use_rezero = False, # use rezero, from 'Rezero is all you need' paper
ff_glu = True, # use GLU variant for feedforward
emb_dropout = 0.1, # embedding dropout
ff_dropout = 0.1, # feedforward dropout
attn_dropout = 0.1, # post-attn dropout
local_attn_heads = 4, # 4 heads are local attention, 4 others are global performers
local_window_size = 256, # window size of local attention
rotary_position_emb = True, # use rotary positional embedding, which endows linear attention with relative positional encoding with no learned parameters. should always be turned on unless if you want to go back to old absolute positional encoding
shift_tokens = True # shift tokens by 1 along sequence dimension before each block, for better convergence
)
x = torch.randint(0, 20000, (1, 2048))
mask = torch.ones_like(x).bool()
model(x, mask = mask) # (1, 2048, 20000)