机器人导航路径平滑算法：一条符合机器人运动限制的路径

文章转自帅气的为为 https://zhuanlan.zhihu.com/p/364421182

介绍

机器人通过栅格地图进行路径规划时，根据静态障碍物得到全局路径，本阶段暂不考虑动态障碍物。通过各种路径规划算法，如 Dijkstra’s，A*，D-star，RRT等，规划出的路径都存在直线之间有急剧拐弯（曲率变化大）的问题。

尽管通过将八邻域改为更多邻域，如前文所述，能略微改善曲率变化急剧的问题，但是这样的路径仍然不适于机器人运动模型，尤其是非全向机器人，如阿克曼底盘，所以需要一条符合机器人运动限制的路径。

路径连续性

连续性包括两个部分：几何连续 $G^i$ ，参数连续 $C^i$ 。

几何连续指路径的多个片段的起始点相连，而且切向量的方向相同。

参数连续指路径的多个片段的起始点相连，而且切向量的方向和大小相同。

如果两曲线在点 $p$ 处的第 $i$ 阶导数相等，那么该两曲线在点 $p$ 处是 $C^i$ 连续，同时也是 $C^k$ 连续的，对于 $\forall k\leq i$ 。总之，曲线 $s$ 的 $n$ 阶导数 $\frac{d^ns}{dt^n}$ 是连续的话，则是 $C^n$ 连续曲线。

如上所述，参数连续意味着曲线和其参数化的平滑，而集合连续仅意味着机器人轨迹平滑。例如 $C^1$ 连续意味着切向量连续，而 $G^1$ 连续意味着斜率连续； $C^2$ 连续意味着加速度矢量连续，而 $G^1$ 连续意味着曲率连续。对于机器人运动来说， $C^1$ 连续保持速度， $C^2$ 连续保持加速度。对于机器人路径规划来说，关键是路径是否 $C^1$ 或者 $C^2$ 连续。高阶连续如 $C^3$ 主要处理面，用于 CAD/CAM 设计。

插值法

多项式插值

对于 $n$ 个点 $(x_1,y_1=f(x_1)),(x_2,y_2=f(x_2)),\cdots,(x_n,y_n=f(x_n))$ ，可以用拉格朗日（Lagrange）插值 $P(x)$ ，其阶 $\leq (n-1)$ ：

$P(x)=\sum_{j=1}^{n}{P_j(x)}$ ，其中 $P_j(x)=y_i\prod_{k=1,k\neq j}^{n}\frac{x-x_k}{x_j-x_k}$ 。

另一种是赫米特（Hermite）插值，定义 $n$ 阶的 $p(x)$ 在 $x_1,x_2,\cdots,x_n$ 处为0：

$h_i^{(1)}(x)=[1-\frac{p''(x_i)}{p'(x_i)}(x-x_i)][p-i(x)]^2$ ， $h_i^{(2)}(x)=(x-x_i)[p-i(x)]^2$ ，其中 $p_i(x)=\frac{p(x)}{p'(x_i)(x-x_i)}$ 。

插值法用于路径平滑十分原始，有两个缺点：计算复杂度高；Runge’s 现象。

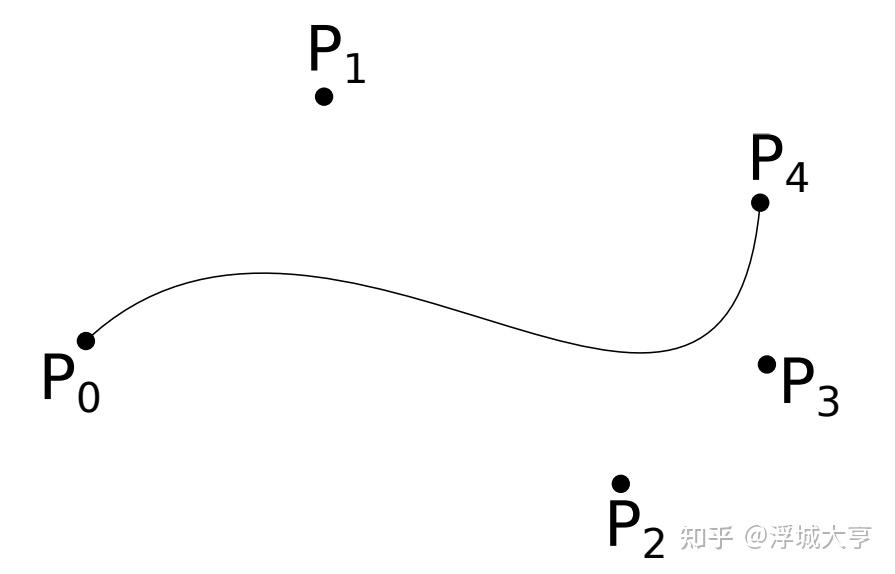
2. 贝塞尔曲线

对于 $n+1$ 个点 $P_0,P_1,\cdots,P_n$ ，对应的贝塞尔曲线定义为：

$\\C(t)=\sum_{i=0}^{n}{P_iB_{i,n}(t)}$ ，其中 $B_{i,n}(t)=( \begin{matrix} n \\\ i \end{matrix} ) t^i(1-t)^{n-i}$ ， $( \begin{matrix} n \\\ i \end{matrix} ) = \frac{n!}{i!(n-i)!}$ 。

3. 三次样条曲线

样条曲线适合于对任意方程建模，对于低阶曲线也有较好的效果，能防止 Runge’s 现象。

有两个重要特点：用最小阶数就可以产生 $C^2$ 近似；对于小曲率也是足够平滑。

考虑 $[a,b]$ 区间内有序的 $n+1$ 个点 $a=x_0<x_1<\cdots<x_n=b$ ，以及相应的分析 $f_i$ ， $i=0,\cdots,n$ 。因为该样条曲线是3阶的，其二阶导数必须是连续的，因此定义 $f_i=s_3(x_i)$ ， $m_i=s_3'(x_i)$ ， $M_i=s_3''(x_i)$ ，于是有：

$\\s_{3,i-1}(x)=M_{i-1}\frac{(x_i-x)^3}{6h_i}+M_{i}\frac{(x-x_{i-1})^3}{6h_i}+C_{i-1}(x-x_{i-1})+\tilde{C}_{i-1}$

其中 $h_i=x_i-x_{i-1}$ ， $i=0,\cdots,n$ ，并且

$\\\tilde{C}_{i-1}=f_{i-1}-M_{i-1}\frac{h_i^2}{6},C_{i-1}=\frac{f_i-f_{i-1}}{h_i}-\frac{h_i}{6}(M_i-M_{i-1})$ $M_i$ 可以从 $M$ 连续系统求得： $\mu_iM_{i-1}+2M_i+\lambda_iM_{i+1}=d_i$ 。

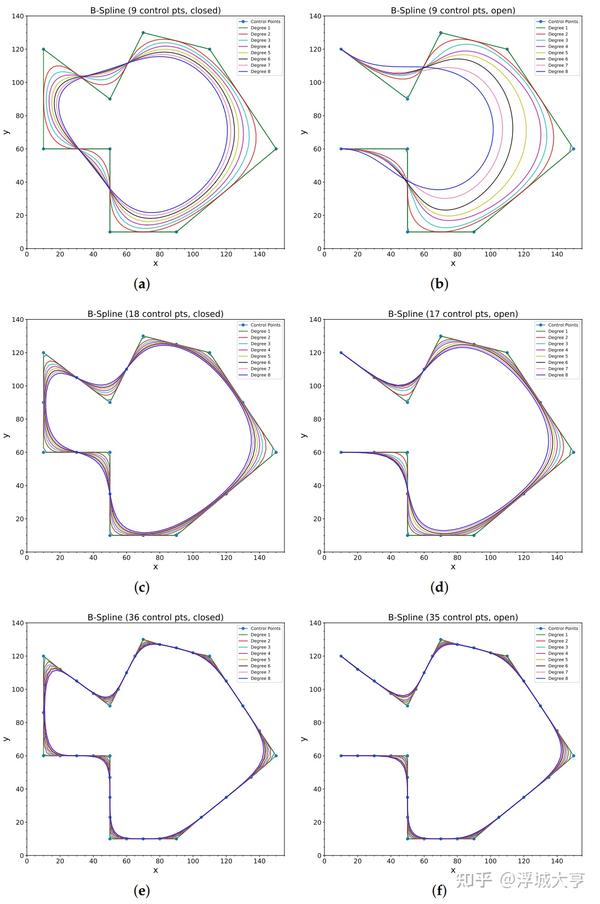
4. B样条曲线

给定 $m$ 个实数 $x_i$ ， $i\in [0,m-1]$ ， $n$ 阶的 B 样条曲线：

$\\S:[x_0,x_{m-1}]\rightarrow \mathbb{R}^2$

由基本的 $n$ 阶 B 样条曲线 $b_{i,n}$ 线性组成：

$\\S(x):\sum_{i=0}^{m-n-2}{P_iB_{i,n}(x)},x\in[x_n,x_{m-n-1}]$

其中 $P_i$ 称为控制点， $m-n-1$ 个控制点形成一个凸包（convex hull），对于 $j\in[0,m-2]$ 这些基本 B 样条曲线定义为：

$\\B_{j,n}(x)=\frac{x-x_j}{x_{j+n}-x_i}B_{j,n-1}(x)+\frac{x_{j+n+1}-x}{x_{j+n+1}-x_{j+1}}B_{j+1,n-1}(x)$

当控制点的个数比阶数多一个时，例如 $x_0=\cdots=x_n=0$ ， $x_{n+1}=\cdots=x_{2n}=1$ ，B 样条曲线退化为贝塞尔曲线。

5. NURBS 曲线

直接给定义：

$\\C(t)=\frac{\sum_{i=0}^{n}{N_{i,p}(t)w_iP_i}}{\sum_{i=0}^{n}{N_{i,p}(t)w_i}}$

其中 $p$ 是阶数， $N_{i,p}$ 是 B 样条曲线基本方程， $P_i$ 是控制点， $P_i$ 的权重 $w_i$ 是齐次点 $P_i^w$ 的最后一个维度。

特殊曲线

Dubin’s 曲线

给定平面内两点和运动方向，Dubins 用圆弧和线段在给定曲率范围内找到连接各点的最短平滑路径，如图所示。

Durbin’s 曲线简单但是有效，适用于实时处理因为计算简单，可以用于回环线来满足各种不同限制。

首先介绍一个简单的车，如图所示。

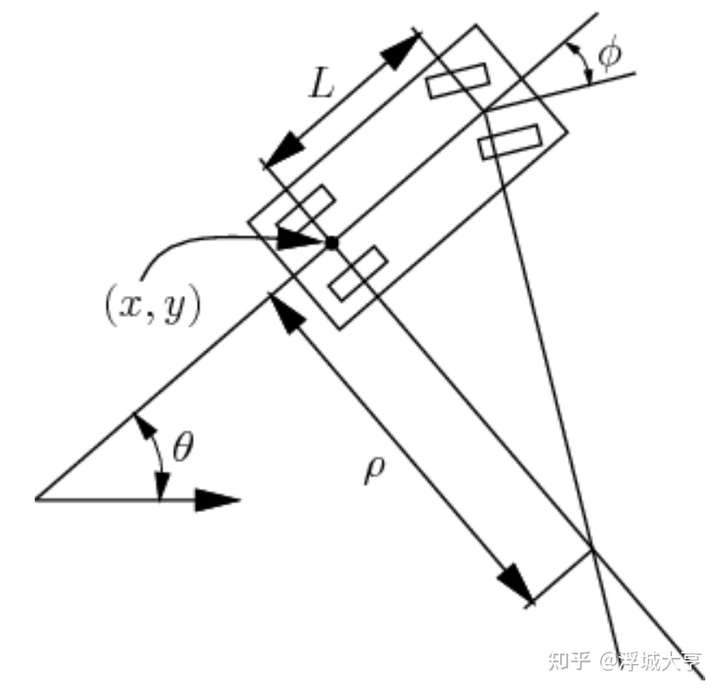
它的 C 空间 $C=\R^2 \times \mathbb{S}^1$ ，定义为 $q(x,y,\theta)$ ，车子运动方程如下：

$\\\dot{x}=f_1(x,y,\theta,s,\phi) \\\dot{y}=f_2(x,y,\theta,s,\phi) \\\dot{\theta}=f_3(x,y,\theta,s,\phi)$

时间间隔 $\Delta t$ 极小时，车子大致走后轮指向。 $\Delta t$ 趋近于0，意味着 $dy/dx=tan\theta$ ，因为 $dy/dx=\dot{y}/\dot{x}$ ， $tan\theta=sin\theta/cos\theta$ ，于是有：

$\\-\dot{x}sin\theta+\dot{y}cos\theta=0$

要满足该限制，方程的解为： $\dot{x}=scos\theta$ ， $\dot{y}=ssin\theta$ ， $s$ 为常数。

下面解关于 $\dot{\theta}$ 的方程， $\rho$ 为汽车转弯半径， $dw=\rho d\theta$ ，因为 $\rho=L/tan\phi$ ，有

$\\d\theta=\frac{tan\phi}{L}dw$

两边同时除以 $dt$ ，因为 $\dot{w}=s$ ，有

$\\\dot{\theta}=\frac{s}{L}tan\phi$

假定速度 $s$ 和转向角 $\phi$ 等同于动作参数 $u_s$ 和 $u_{\phi}$ ，动作向量 $u=(u_s,u_{\phi})$ ，汽车动力学方程为：

$\\\dot{x}=u_scos\theta \\\dot{y}=u_ssin\theta \\\dot{\theta}=\frac{u_s}{L} tanu_{\phi}$

因为车子有最小转弯半径 $\rho _{min}$ ，而路径规划的任务是最小化起点到终点的车子运动曲线，如果 $\rho _{min}=0$ 那么就没有曲率限制，走两点间直线距离最短，但实际上需要优化

$\\L(\widetilde{q},\widetilde{u})=\int_{0}^{t_F}\sqrt{\dot{x}(t)^2+\dot{y}(t)^2}dt$

，其中 $t_F$ 是到达终点 $q_G$ 的时间，如果没有到达则 $L(\widetilde{q},\widetilde{u})=0$ 。

因为速度恒定，运动方程可以简化为：

$\\\dot{x}=cos\theta \\\dot{y}=sin\theta \\\dot{\theta}=u$

其中 $u$ 属于区间 $U=[-tan\phi_{max},tan\phi_{max}]$ ，对于 $\phi_{max}\in(0,\pi/2)$ ，以下结果都成立：

Symbol	Steering: u
S	0
L	1
R	-1

在[1]中已经证明，在任何两个空间之间，Dubins 汽车的最短路径可以由不超过三个基本运动的组合表示，所以动作空间为 $u\in\left\{ -1，0，1 \right\}$ ，只有如下六个关键词是最优的：

$\\\left\{ LRL,RLR,LSL,LSR,RSL,RSR \right\}$

为了更加准确，要表示每个基本动作的持续时间。对于 $L$ 或 $R$ ，加入下标表示转角，对于 $S$ ，加入下标表示距离，因此 Dubins 曲线可以更加精确的表示为：

$\\\left\{ L_{\alpha}R_{\beta}L_{\gamma}, R_{\alpha}L_{\beta}R_{\gamma}, L_{\alpha}S_dL_{\gamma}, L_{\alpha}S_dR_{\gamma} ,R_{\alpha}S_dL_{\gamma}, R_{\alpha}S_dR_{\gamma} \right\}$

其中 $\alpha,\gamma \in [0,2\pi)$ ， $\beta \in (\pi,2\pi)$ ， $d\ge0$ 。如图所示两种可能情况。

也可以用 $C$ 来代表曲线，即 $R$ 或 $L$ ，那么6个词可以简化为仅2个词：

$\\\left\{ CCC,CSC \right\}$

更准确的版本为： $\\\left\{ C_{\alpha}C_{\beta}C_{\gamma},C_{\alpha}S_dC_{\gamma} \right\}$

当 $\theta=\pi$ 时，分割如下图所示：

已有了关键信息，但是对于给定的 $q_I$ 和 $q_G$ ，仍存在两个问题：

六个词中哪些可以生成最短路径？

对于某个词，相应下标的值 $\alpha$ ， $\beta$ ， $\gamma$ 是多少？

一个简单的方法就是穷举法，如图所示。

2. Clothoid

Clothoid，也被称为欧拉螺旋线或者 Cornu’s 螺旋线，表示在复平面：

$\\B(t)=S(t)+iC(t) \\x(t)=C(t)=\int_{0}^{t}cos(\frac{\pi}{2}s^2)ds \\y(t)=S(t)=\int_{0}^{t}sin(\frac{\pi}{2}s^2)ds$

其中 $C$ 和 $S$ 是菲涅尔函数，有时候也成为菲涅尔余弦积分和菲涅尔正弦积分。

当 $t\rightarrow \infty$ 时两个菲涅尔函数都趋近于 $\frac{1}{2}$ ，所以这个曲线逐渐趋近于第一象限 $(\frac{1}{2},\frac{1}{2})$ ，对称的来说，因为两个方程都是奇函数，这个曲线逐渐趋近于第一象限 $(-\frac{1}{2},-\frac{1}{2})$ 。

Cornu’s 螺旋线的曲率和曲线距离成正比，因此车子的角加速度恒定，意味着驾驶员匀速转动方向盘即可，更加安全。

3. Hypocycloid

当一个半径 $r_s$ 小圆在大一点的半径 $R_L$ 大圆内滚动时，小圆上的某固定点产生：

$\\x(\theta)=(R_L-r_s)cos(\theta)+r_s\cdot cos(\frac{R_L-r_s}{r_s})\theta \\y(\theta)=(R_L-r_s)sin(\theta)-r_s\cdot sin(\frac{R_L-r_s}{r_s})\theta$

其中 $\eta$ 是峰点（曲线不可导的地方）的个数， $\zeta$ 是两圆半径比即 $\zeta=\frac{r_s}{R_L}$ ，例子如图所示

如果在 hypocycloid 内有 $n$ 个峰点，小圆半径则为 $r_s=\frac{R_L}{n}$ ，因为小圆转 $n$ 圈回到原点，也就生成 $n$ 个峰点。

有一种新的方法成为 Smooth Hypocycloidal Paths（SHP），可以生成任何角度，该算法用来尽量保持直线路径，只平滑急转弯处，例子如图所示

4. Reeds-Shepp Curves

和 Dubins 相似，直接给运动方程：

$\\\dot{x}=u_1cos\theta \\\dot{y}=u_2sin\theta \\\dot{\theta}=u_1u_2$

其中 $u_1\in\left\{ -1,1 \right\}$ ， $u_2\in \left\{ -tan\phi_{max},tan\phi_{max} \right\}$ 。第一个变量 $u_1$ 决定变速箱向前（ $u_1=1$ ）或向后（ $u_1=-1$ ），为了简化假定 $u_2\in[-1,1]$ ，对于所有 $\phi_{max}\in(0,\pi /2)$ 都成立。

因此词袋为：

$\left\{ C|C|C,CC|C,C|CC,CSC,CC_{\beta}|C_{\beta}C,C|C_{\beta}C_{\beta}|C,C|C_{\pi/2}SC,CSC_{\pi/2}|C,C|C_{\pi/2}SC_{\pi/2}|C \right\}$

其中 $|$ 表示变速箱逆向，即向前到向后，或向后到向前。

下图举例 $R_{\alpha}^+L_{\beta}^-R_{\gamma}^+$ 。

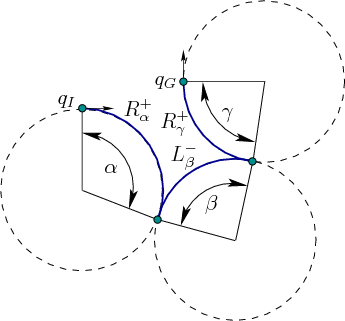
下表为 Reeds and Shepp 的48种不同曲线，然而第一行的 $L^- R^+ L^-$ 和 $R^- L^+ R^-$ 可以被剔除，因此只有46种。

5. Balkcom-Mason 曲线

将动作集定义为 $U=[-1,1]\times[-1,1]$ ，优化方程

$\\L(\widetilde{q},\widetilde{u})=\int_{0}^{t_F}\sqrt{\dot{x}(t)^2+\dot{y}(t)^2}+|\dot{\theta}(t)|dt$

因此可以有四个基本运动：

可证明得出最短路径最多由五个基本部分组成，因此有9个词即：

准确形式由下表给出：

为了显示的更易懂，给出九种运动模型图：

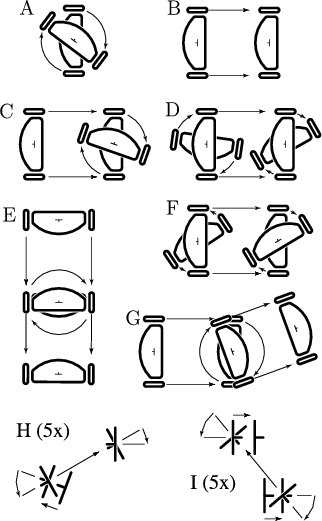
当 $q_I=(x,y,\frac{\pi}{4})$ ， $q_G=(0,0,0)$ 时，最优曲线如图所示：

[1] Dubins, L.E. (1957) On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. American Journal of Mathematics, 79, 497-516.