Neural ODE 神经常微分方程

Neural ODE

ODE常微分方程
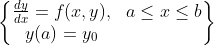
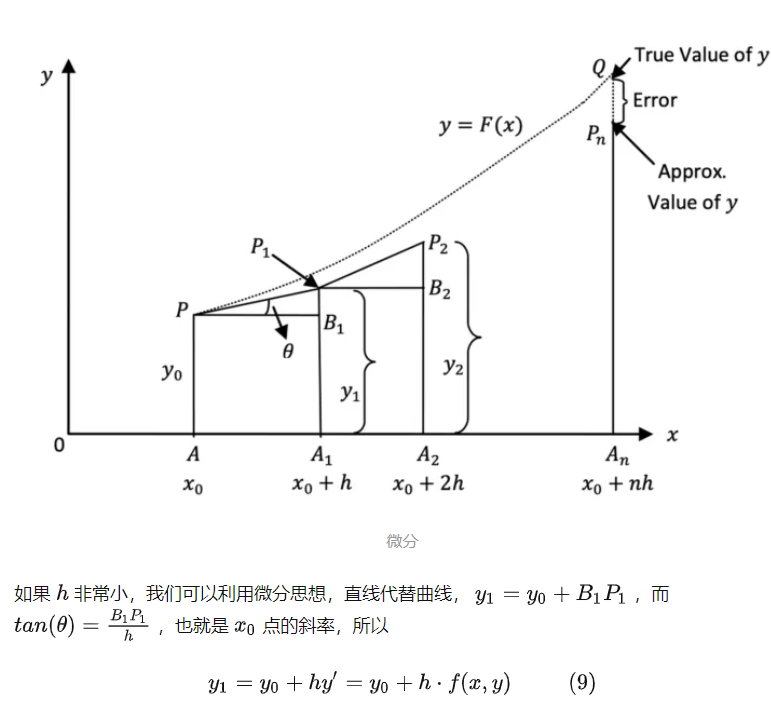
欧拉法求解：欧拉法求解过程是一个递归的过程，这个思想和牛顿法、梯度下降法是相似的。并且它将函数离散化，分割成一个个小段来求解。欧拉法求解的常微分方程的形式通常为在这里插入图片描述

图片来自知乎Neural ODE，这个世界终究是连续的

使用欧拉法解方程的例子：摘自欧拉法（Euler‘s method）求常微分方程(ODE)近似解
在这里插入图片描述
代码：

import numpy as np
import matplotlib.pyplot as plt
y0=1 #初始条件
def f(x,y):
    return y-2*x/y
def Eular(y0,n,f):
    y=[y0] #储存各个点的函数值
    y0=y0
    for x in np.linspace(0,1,n):
        '''求函数在区间[0,1]近似解，分n份'''
        y1=y0+f(x,y0)/n
        y.append(y1)
        y0=y1
    return y
y=Eular(1,10,f=f)
x=np.linspace(0,1,len(y))
plt.plot(x,y,color='blue')
plt.show()

神经常微分方程：
在这里插入图片描述
求解常微分方程时，可以用ODEsolver。它就相当于是计算器，我们给出初始to,h(t0),神经网络，要求的时间t ，它就可以自动求解。

ODEsolver本质上就是用数值解法一步步求解到T。数值法求wi+1是由wi加上步长h*区间上的平均变化率。不同的算法，对平均变化率的取法不同。
Euler方法的平均变化率取的ti点的导数
改进Euler：
先由当前点用欧拉法求出下一点wi+1’的值，再用当前点梯度和预报点梯度的平均作为区间平均变化率求解真正wi+1点的值。
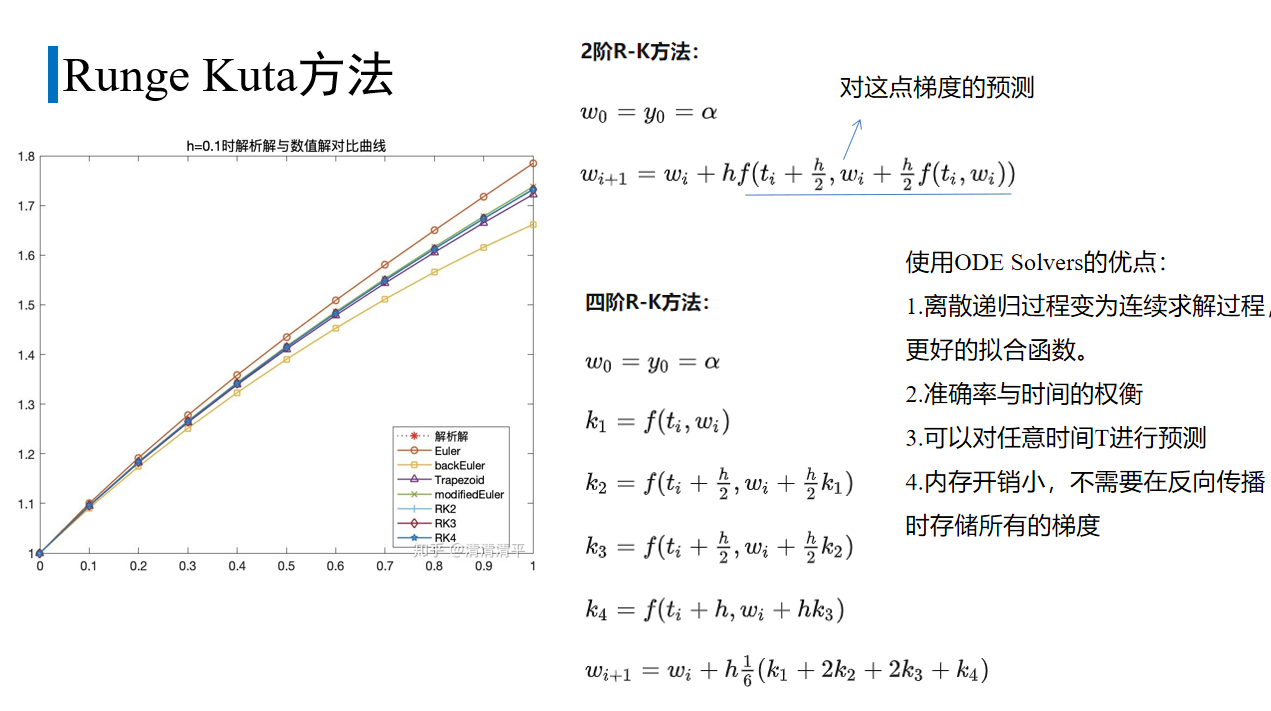
在这里插入图片描述
龙格-库塔方法比Euler有更高的精度。
rk2:
先用欧拉法估计h/2处的梯度，再用这个值计算wi+1。

rk4:
wi+1由wi和四个梯度的加权平均确定，步长 h。
k 1 是这一步开始处使用欧拉方法的导数；
k 2 是 h/2 处的导数，在 k 1基础上；
k 3 依旧是 h/2 处的导数，在k2基础上；
k 4 是在k3基础上终点h 处的导数。
几种数值解法和真实解的对比，RK方法的准确率比较高。

一般的反向传播算法要保存前向计算过程中的activation激活图。而ODE使用adjoint method (伴随方法)，不需要保存激活图也能计算梯度。
因为伴随方法把反向过程看作一个新的ODE初值求解问题 (IVP)，直接用ODE Solver计算得到梯度值。这样减少内存占用。

应用：

最近的研究发现梯度下降算法的迭代过程(GDA) 可以看作是常微分方程 (ODE) 的欧拉离散化。
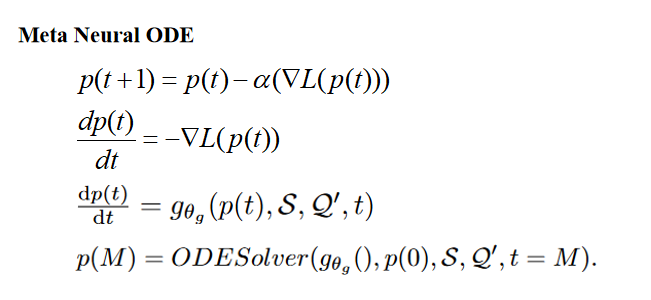
在这里插入图片描述
设计一个网络来估计我们要求的参数的梯度，这里是原型p。
有了估计的梯度后，使用odesolver求解p在指定时刻的值。这个指定时刻M由训练阶段使损失收敛的超参决定。

Neural ODE 神经常微分方程

Neural ODE

猜你喜欢