同余定理
我们在《密码学学习笔记二:RSA加密法》里面提到过同余,此处把同余作为补充知识,单独写一篇文章讲解一下。
同余定理是数论中的重要概念。给定一个正整数m,如果两个整数a和b满足(a-b)能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。
举个例子,a=7,b=4,m=3.a≡b(mod m),因为7 mod 3=1;4 mod 3=1;并且(7-4)/ 3 = 1,能被3整除。
那么在上一节RSA加密算法中,
(1)公钥(e,N)=(3,33);
(2)私钥
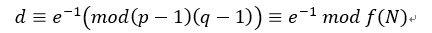
又因为e≡e(mod f(N))肯定成立;
所以,根据同余定理的性质同乘性:
若a ≡ b(mod m),则 a * c ≡ b * c(mod m)
若a ≡ b(mod m),c ≡ d(mod m),则 a * c ≡ b * d(mod m)
所以,可以得出 e×d≡1 mod f(N);
显而易见,不管f(n)取什么值,符号右边1 mod f(n)的结果都等于1;符号的左边d与e的乘积做模运算后的结果也必须等于1。
穷举,求出d = 7;
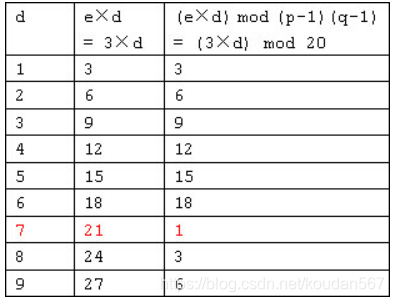
私钥(d,N)=(7,33);
(3)加密:假设要加密的密文m = 5;公钥(e,N)=(3,33);

C ≡ 5^3 mod 33
因此(125-C)/ 33 可以整除,当商为3时,C= 26;
因此被加密过的信息为26。
(4)解密,私钥(d,N)=(7,33);C = 26
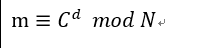
m ≡ 26^7 mod 33
因此 (26^7 - m )/ 33 可以整除,商为243388186时,同理求得m = 5.
至此,整个RSA加解密的过程结束。