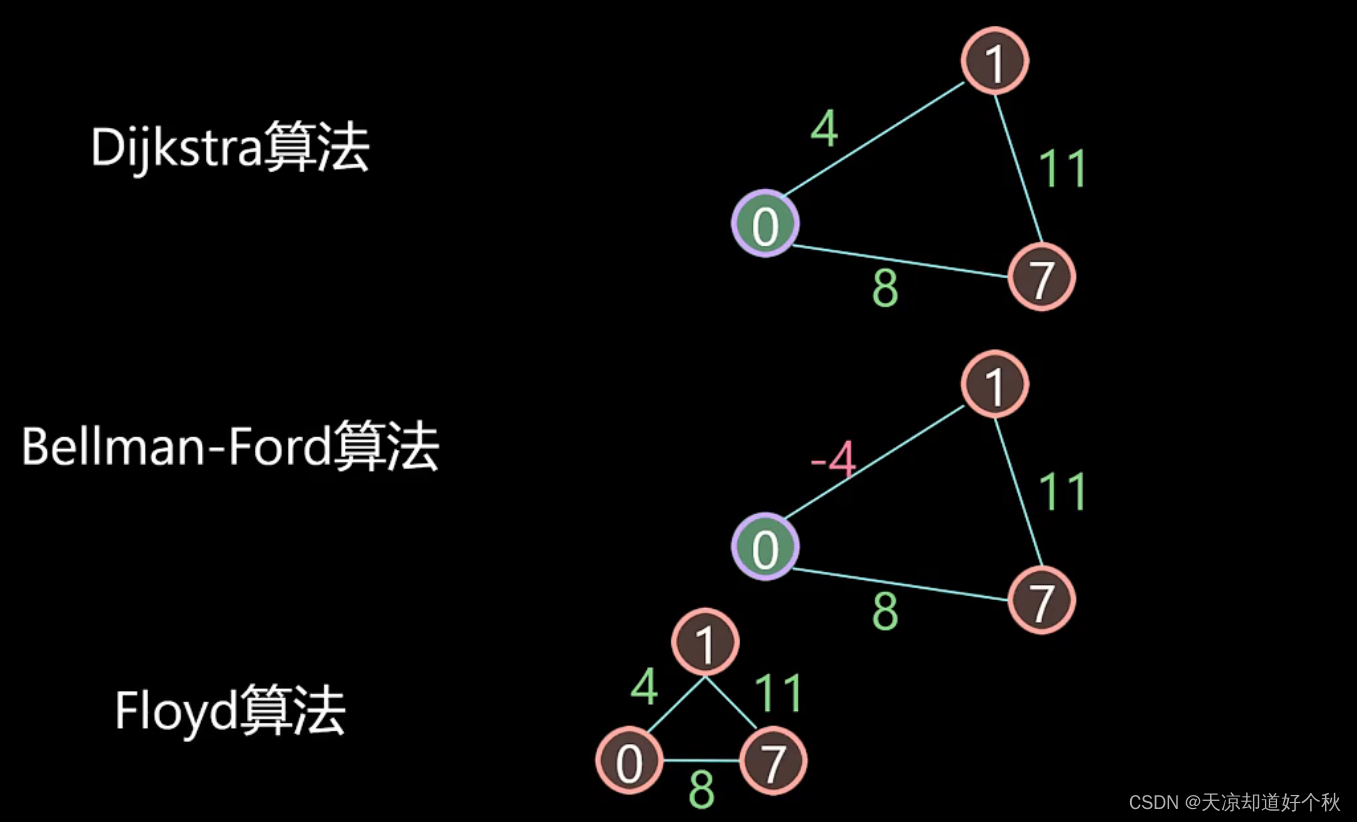
文章目录
前言
本系列文章主要记录学习路径规划算法过程中的一些知识点;
主要学习视频源自B站大学 小黎的Ally 的 《路径规划与轨迹跟踪系列算法》,视频链接如下:视频链接
文章参考:链接一、链接二
一、迪杰斯特拉(Dijkstra)
算法介绍
- 迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
主要特点:
- 是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
- Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题。
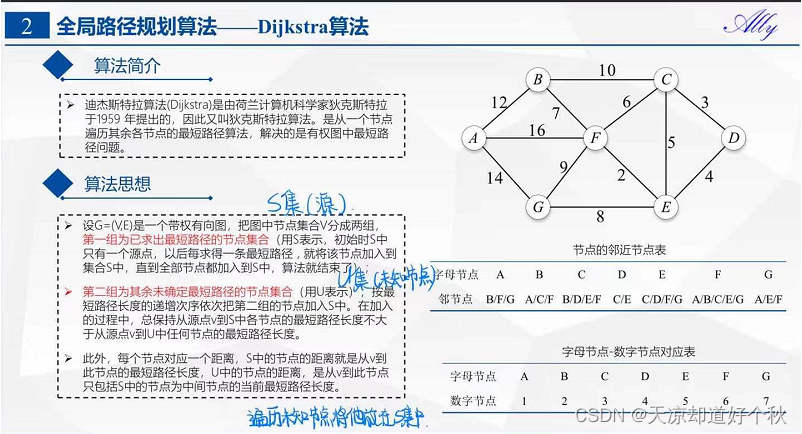
基本思想

通过Dijkstra计算图中的最短路径时,需要指定起点s(即从源点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;
U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。
然后,从U中找出路径最短的顶点,并将其加入到S中;
接着,更新U中的顶点和顶点对应的路径。
然后,再从U中找出路径最短的顶点,并将其加入到S中;
接着,更新U中的顶点和顶点对应的路径。
…
重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"
[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
二、图解
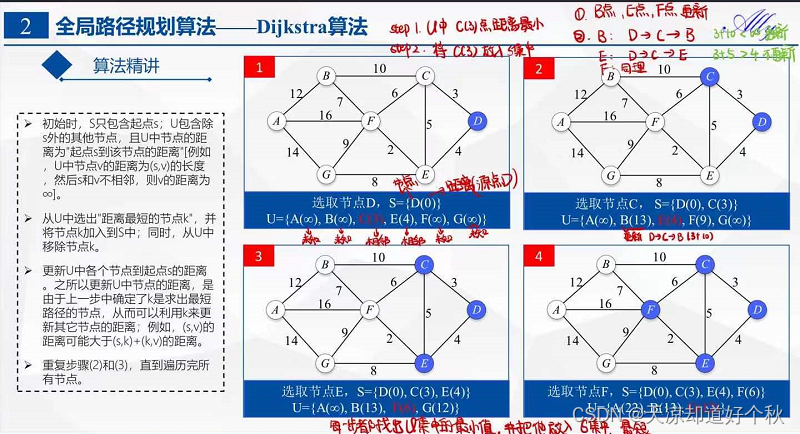
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:选取源点
选取源点D加入S集中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3;∞表示未知距离。
第2步:找出最短距离点,加入S集,并更新U集
从U集中选出距离最短的节点C
将节点C加入到S集中,同时从U集中删除C。
上一步操作之后,U中节点C到源点D的距离最短;因此,将C加入到S中,同时更新U中节点的距离。以节点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:选取U集最小距离点,加入S集,更新U集
将节点E加入到S中。
上一步操作之后,U中节点E到源点D的距离最短;因此,将E加入到S中,同时更新U中节点的距离。还是以节点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。因此更新F点距离;
此时,S={D(0),C(3),E(4)}, U={A(∞),B(13),F(6),G(12)}。
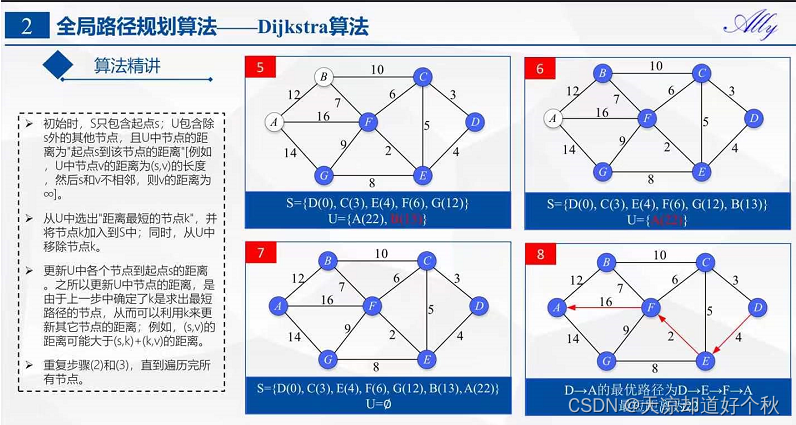
第4步:选取U集最小距离点,加入S集,更新U集
将节点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:选取U集最小距离点,加入S集,更新U集
将节点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:选取U集最小距离点,加入S集,更新U集
将节点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:选取U集最小距离点,加入S集,更新U集
将节点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。U={空集}
此时,源点D到各个节点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。即D→A的最优路径为D→E→F→A最短距离为22
三、编程实现
代码如下:
#include<iostream>
#include<string>
using namespace std;
const int MAX = 10; //限定最大的顶点数
const int _INFINITY = 65535; //定义无穷大
class Graph
{
private:
int vertex_num; //顶点数
int edge_num; //边数
int weight; //权值
string vertex[MAX]; //顶点数组
int edge[MAX][MAX]; //邻接矩阵
int locate(string ch); //定位
int *final; //标识是否已纳入最短路径,置为1表示纳入
int *distance; //存放最短路径的权值和
string *path; //存放最短路径字符串
public:
Graph(int v_n, int e_n); //构造函数
void print_graph(); //打印邻接矩阵
void Dijkstra(int v); //Dijkstra算法
int Min(int *_distance, int num); //最小值
};
//定位(找到字母的下标)
int Graph::locate(string ch)
{
int index;
for (index = 0; index < this->vertex_num; index++)
{
if (this->vertex[index] == ch)
{
break;
}
}
return index;
}
//构造函数
Graph::Graph(int v_n, int e_n) : vertex_num(v_n), edge_num(e_n)
{
int i, j, k;
cout << "现在请输入这" << this->vertex_num << "个顶点:" << endl;
for (i = 0; i < this->vertex_num; i++)
{
cin >> this->vertex[i];
}
//初始化邻接矩阵
for (i = 0; i < this->vertex_num; i++)
{
for (j = 0; j < this->vertex_num; j++)
{
if (i == j)
{
this->edge[i][j] = 0;
}
else
{
this->edge[i][j] = _INFINITY;
}
}
}
cout << "请依次输入边相邻的两个顶点及边的权值:" << endl;
for (k = 0; k < this->edge_num; k++)
{
string first, second;
cin >> first >> second >> this->weight;
i = this->locate(first);
j = this->locate(second);
edge[i][j] = this->weight;
//无向图
edge[j][i] = this->weight;
}
}
//打印
void Graph::print_graph()
{
cout << "邻接矩阵为:" << endl;
for (int i = 0; i < this->vertex_num; i++)
{
for (int j = 0; j < this->vertex_num; j++)
{
cout << this->edge[i][j] << "\t";
}
cout << endl;
}
}
//返回最小值下标
int Graph::Min(int *_distance, int num)
{
int index = 0, min = _INFINITY;
for (int i = 0; i < num; i++)
{
if (!this->final[i] && _distance[i] < min)
{
min = _distance[i];
index = i;
}
}
return index;
}
//Dijkstra算法
void Graph::Dijkstra(int v) //从源点v出发
{
int i, j, min;
this->path = new string[MAX];
this->final = new int[MAX];
this->distance = new int[MAX];
//初始化上列数组
for (i = 0; i < this->vertex_num; i++)
{
this->final[i] = 0;
this->distance[i] = this->edge[v][i]; //初始化为源点到各t'hi点的权值大小
if (this->distance[i] != _INFINITY)
{
this->path[i] = this->vertex[v] + this->vertex[i]; //当直接路径存在时,同样初始化为源点到各点的路径
}
else
{
this->path[i] = "";
}
}
//初始化源点
this->distance[v] = 0;
this->final[v] = 1;
//开始主循环,每次求得v到一个顶点的最短路径,所以循环次数比顶点数少一次
for (i = 1; i < this->vertex_num; i++)
{
min = this->Min(distance, this->vertex_num); //求当前最小值下标
cout << "最短路径:" << this->path[min] << "\t权值:" << this->distance[min] << endl; //输出当前最短路径
this->final[min] = 1;
//再次循环,修正当前最短路径及其权值和
for (j = 0; j < this->vertex_num; j++)
{
//如果经过的顶点的路径比现在这条路径还短的话
if (!this->final[j] && this->distance[j] > this->edge[min][j] + this->distance[min])
{
this->distance[j] = this->edge[min][j] + this->distance[min];
this->path[j] = this->path[min] + this->vertex[j];
}
}
}
delete[]path;
delete[]distance;
delete[]final;
}
运行结果
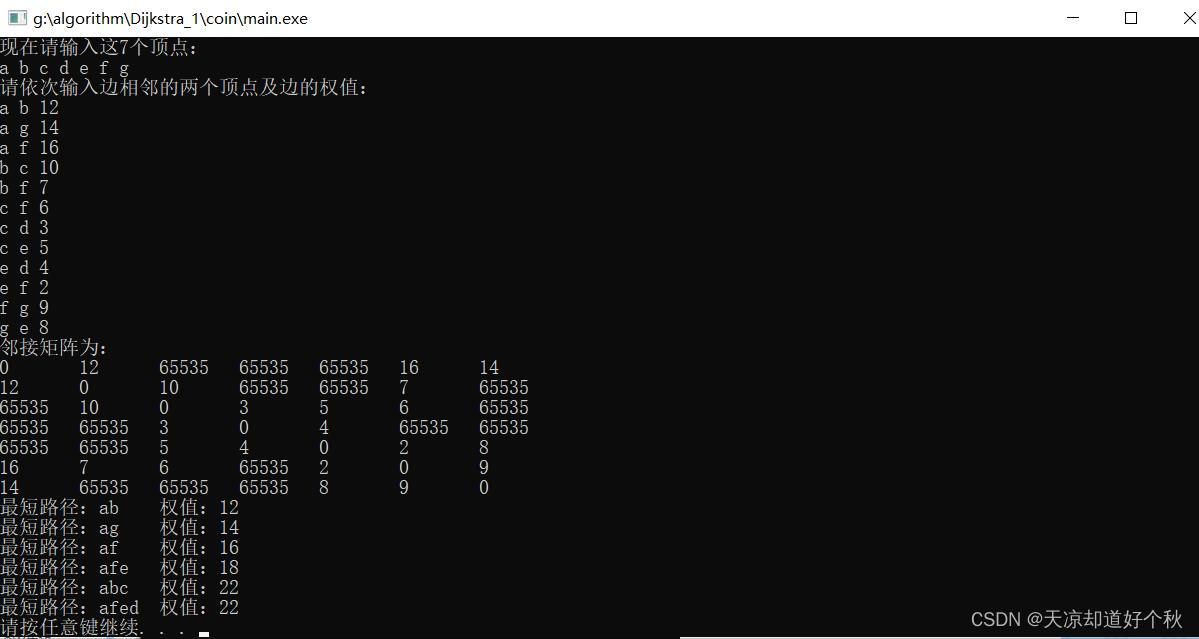
总结
Dijkstra算法其实就是每一步都找出U集合中距离最小的值,将他放入S集中,并在U集中更新数据,再遍历所有节点之后,找到一个终点最小值就是最优路径。
算法最后可以得到一个最优路径树,复杂度较为合理–O(N^2)。
Dijkstra算法边权都为正数,所以不会出现加权为负的情况,因此当前距离最短的点,不可能被其他点更新,即保证每一次check的都是最短距离点。
每次选用距离较短的点,更新其他点的距离。因为直接去某点可能距离不如绕路近。
Dijkstra算法边权皆为正数,如果存在负数则需要Bellman-Ford算法,如果想要求任意两点之间的最短距离选择Floyd算法。