数据结构与算法(一)——时间复杂度

为什么需要时间复杂度分析?

通过统计、监控，就能得到算法执行的时间和占用的内存大小，但是，这种统计方法
有很多不足,例如：

1. 测试结果依赖测试环境，例如测试PC的电脑的芯片从i7换为i5,那么运行时间就会增加
2. 测试结果依赖测试数据规模，例如小规模的数据排序，插入排序比快速排序快

时间复杂度的表示方法

大O表示法（重要）

定义：当且仅当存在两个参数 c > 0 ，n0 > 0, 对于所有的 n >= n0 ， 都有 f(n) <= cg(n),则
f(n) = O(g(n)),如图：

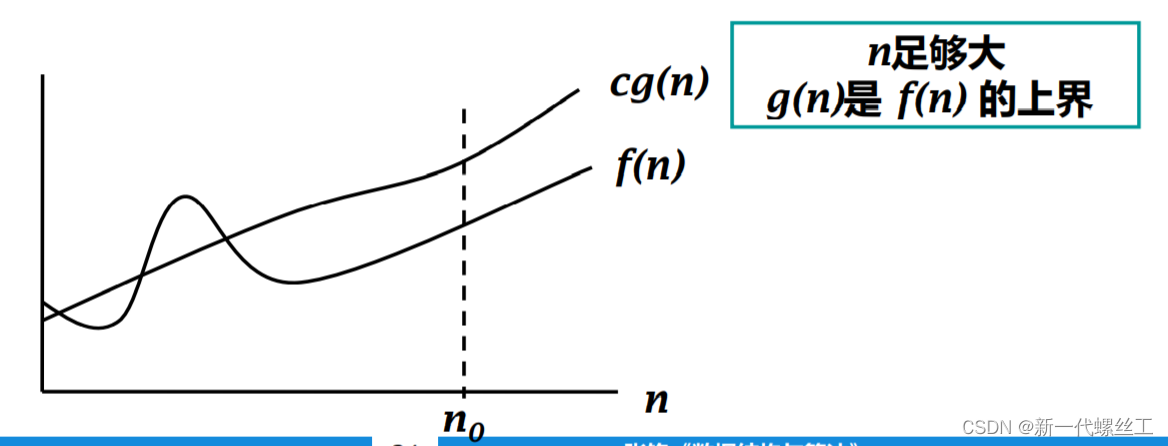
用大O表示法表示时间复杂度示例：

 int cal(int n) {
    
    
 int sum = 0;
 int i = 1;
 int j = 1;
 for (; i <= n; ++i) {
    
    
       j = 1;
       for (; j <= n; ++j) {
    
    
       sum = sum + i * j;
     }
 }
 return sum;
 }

假设上述代码，执行一行代码的时间为 t ,则花费的总时间为 (2*n^2+2*n+4)*t。当 n 非常大时，上述代码花费的时间
只取决于 n^2 ,即 T(n) = O(n^{2)，上述代码的时间复杂度为O(n}2)

简单说：大O表示法就是忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级

大Ω表示法（了解即可）

定义 ：如果存在正数 c 和 n0 ，使得对所有的 n >= n0 ，
都有 f(n) >= cg(n)，则 f(n) = Ω(g(n)) ，如图：

大θ表示法（了解即可）

定义：如果一个函数既在集合 O (g(n)) 中又在集合 Ω(g(n))
中，则称其为 θ(g(n))。也即，当上、下限相同时则可用大 θ 表示法，如图：

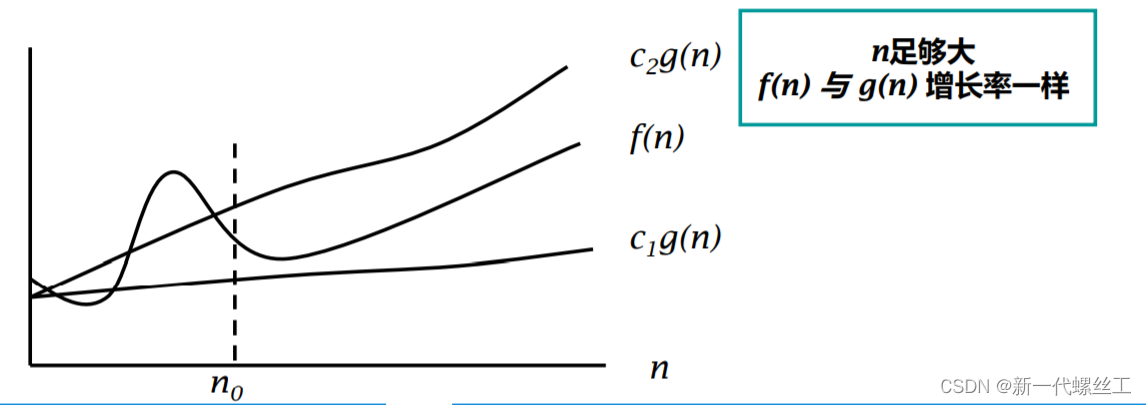
常用的时间复杂度量级

1. 常数阶 O(1)

O(1)只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。比如这段代码，即便有3行，它的时间复杂度也是O(1），
而不是O(3)。

 int i = 8;
 int j = 6;
 int sum = i + j;

只要代码的执行时间不随n的增大而增长，这样代码的时间复杂度我们都记作O(1)。或者说，一般情况下，只要算法中不存在循环语句、递归语
句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

2. 对数阶 O(logn)
3. 线性阶 O(n)
4. 线性对数阶 O(n * logn)
5. 平方阶O(n^{2)，立法阶O(n}3)，k方阶O(n^k)等
6. 指数阶 O(2^n)
7. 阶乘阶 O(n!)

时间复杂度分析

计算运行次数确定

一些算法的时间复杂度可以简单地通过计算其运行次数来确定。

示例1,计算两个数组和的算法：

int count(int[] array1,int m,int[] array2,int n){
    
    
  int sum = 0;
  for(int i = 0;i < m;i++){
    
    //运行 m 次
      sum += array1[i];
  }
  for(int i = 0;i < n;i++){
    
    //运行 n 次
      sum += array2[i];
  }
  return sum; 
}

由于m、n不相等，其执行次数为 m+n，所以时间复杂度为 O(m+n)

示例2，冒泡排序算法：

  private static void sort(int[] data){
    
    
        if(data.length <= 1)return;
        int n = data.length;
        for (int i = 0; i < n; i++) {
    
    
            for (int j = 0; j+1 < n - i; j++) {
    
    
                if(data[j] > data[j+1]){
    
    
                    int cache = data[j];
                    data[j] = data[j+1];
                    data[j+1] = cache;
                }
            }
        }
    }

上述代码地运行次数为n*(n+1)/2,由于大O表示法，要去除常量、低阶、系数，所以时间复杂度为O(n^2)

示例3，需要一些数学计算来得到时间复杂度：

 i=1;
 while (i <= n) {
    
    
 i = i * 2;
 }

如代码所示，该程序的执行时间 x 满足 n = 2^0 * 2^1 * 2^2 * … *2^x，即 x = logn，所以时间复杂度为O(logn)

执行树

对于递归函数，递归调用的数量很少与输入的大小呈线性关系。在这种情况下，最好采用执行树，这是一个用于表示递归函数的执行流程的树。树中的每个节点都表示递归函数的调用。因此，树中的节点总数对应于执行期间的递归调用的数量。

下面是leetcode上的斐波那契数编程题。

斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。
该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N，计算 F(N)。

解答代码如下（注意下面的代码可以通过记忆化来优化）

class Solution {
    
    
    public int fib(int N) {
    
    
        if(N == 0) return 1;
        return fib(N-1)+fib(N-2);
    }
}

下面的图示（图片来源leetcode）展现了用于计算斐波纳契数 f(4) 的执行树。

在 n 层的完全二叉树中，节点的总数为 2^n -1。因此 f(n) 中递归数目的上限（尽管不严格）也是 2^n -1。那么我们可以估计该算法的时间复杂度为O(2^n)

其他

最好、最坏、平均情况时间复杂度

示例，找到 x 在数组中的位置:

// n表示数组array的长度
int find(int[] array, int n, int x) {
    
    
 int i = 0;
 int pos = -1;
 for (; i < n; ++i) {
    
    
     if (array[i] == x) {
    
    
         pos = i;
         break;
     }
 }
 return pos;
}

当 x 在数组的 i=0 的位置的时候，该程序就只需要执行一次，时间复杂度为 O(1);

当 x 不在数组的时候，该程序需要遍历数组，时间复杂度为 O(n);

为了表示代码在不同情况下的不同时间复杂度，我们需要引入三个概念：最好情况时间复杂度、最坏情况时间复杂度和平均情况时间复杂度。但是出现最好和最坏时间复杂度的概率小，为了更好地表示平均情况下的复杂度，我们就需要平均情况时间复杂度。

以上述代码为例，存不存在 x 的概率为 1/2,则存在 x 并出现在 0 ~ n-1 位置的概率为 (1+2+…+n)/2n,不存在 x 的概率为 n/2 ，即 (3*n+1)/4,用大O表示法，则时间复杂度为O(n)

均摊时间复杂度

在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂
度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度

为了更全面，更准确的描述代码的时间复杂度，才要引入最好、最坏、平均情况时间复杂度以及均摊时间复杂度。但是只有代码复杂度在不同情况下出现量级差别时才需要区别这四种复杂度。大多数情况下，是不需要区别分析它们的。

常见算法的时间复杂度

面试中常常让你手写代码，顺便问你该算法的时间复杂度是多少，因此记住常见的算法的时间复杂度是十分必要的。

排序算法

排序算法	时间复杂度
冒泡排序	O(n^2)
插入排序	O(n^2)
选择排序	O(n^2)
快速排序	O(nlogn)
归并排序	O(nlogn)
桶排序	O(n)
计数排序	O(n)
基数排序	O(n)

二叉树遍历算法

二叉树遍历算法	时间复杂度
前序遍历（递归实现）	O(n)
前序遍历（迭代实现）	O(n)
中序遍历（递归实现）	O(n)
中序遍历（迭代实现）	O(n)
后序遍历（递归实现）	O(n)
后序遍历（迭代实现）	O(n)

参考

• leetcode递归的时间复杂度分析
• 中国大学mooc——数据结构与算法课程
• 极客时间的《数据结构与算法之美》专栏