[NOIP1999 普及组] Cantor 表
题目描述:
现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的:
1/1 , 1/2 , 1/3 , 1/4, 1/5, …
2/1, 2/2 , 2/3, 2/4, …
3/1 , 3/2, 3/3, …
4/1, 4/2, …
5/1, …
…
我们以 Z 字形给上表的每一项编号。第一项是 1/1,然后是 1/2,2/1,3/1,2/2,…
输入格式:
整数N(1 <= N <= 10^7)。
输出格式:
表中的第 N 项。
样例 #1:
样例输入 #1:
7
样例输出 #1
1/4
思路:
算法1:模拟
模拟,按题意一个个枚举
时间复杂度O(n),可以通过本题n≤10^7.
算法2:枚举
发现Z字形的每条斜线可以快速枚举,即枚举
1/1 , 1/2 , 3/1 , 1/4 , 5/1 , 1/6……找到要求的第n项所在斜线,再一个个枚举或计算得出答案
时间复杂度O(√n),可以通过n≤10^14
算法2.2:枚举简化
枚举第n项在哪一行,计算得出答案,比算法2好写,
时间复杂度同算法2
算法3:二分
发现第i条斜线(即分子分母之和=i+1的所有项)中包含i*(i-1)/2+1至i*(i+1)中的每一项,所以可以二分分子分母之和,再根据分子分母之和的奇偶性直接计算第n项
时间复杂度O(㏒₂n),可以通过n≤10^18,加上高精可通过n≤10^1000
二分算法代码:
#include<iostream>
#include<cmath>
using namespace std;
int main(){
long long l=1,r,mid,n,a;
cin>>n;
r=n;
while(l<r){
mid=(l+r)/2;
if(mid*(mid+1)/2<n)
l=mid+1;
else
r=mid;
}
a=n-l*(l-1)/2;
if(l%2==0)
cout<<a<<'/'<<l+1-a;
else
cout<<l+1-a<<'/'<<a;
return 0;
}当然,最简单的还是“数学”直接推,O(1)复杂度直接起飞,所以我们直接来推一下吧!
算法4:数学直接推
已知数据是求第个。
明显Z形画出来的三角,从左上到右下的行数是从1开始公差为1的等差数列。所以利用求和公式,设行数为的话则有:
因此我们 设使得
根据建立起的函数的递增性,可知
所以通过求根公式求出然后向上取整就可以在O(1)的时间复杂度求出行数了。
Which is 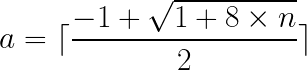
接下来,还要求出所在当行的具体位置,这个就很容易了,只需要知道 到那一行总共有多少个:明显
个
所以要求的也就是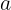 那一行的第
那一行的第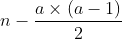 个。
个。
接下来是一个对于知道行数+第几个的Cantor形式求法:
对于第a行,中所有个体,都有(“/”左边)+(“/”右边)
同时 ,
输出的结果应该是:
<u>(_第几个_ )/(a+1- _第几个_ )</u>
<u>而剩下的则“/”两边相反即好。</u>
以上就是O(1)(其实应该没比二分快多少,相当于让系统做了三分而已)解决此题的详解。既然是数学推算,代码就不贴了,没啥意思。
总结:
该题题目很简单,可以用非常简单的算法解决,但是我们可以举一反三,更加深入的思考,想到更牛X,更高效快速的算法。
