递归证明——cycles of curves是必选项？

1. 引言

最早在2014年论文 “Scalable Zero Knowledge via Cycles of Elliptic Curves” (BCTV14) 中提出将cycle of curves用于IVC（Incremental Verifiable Computation）中，以提升递归证明的工作效率。

2. 何为cycles of curves？

令$E_p$为elliptic curve over finite field ${\mathbb{F}}_p$，其中$p$为prime，将其表示为$E_p/{\mathbb{F}}_p$。
group of points of $E_p$ over ${\mathbb{F}}_p$，具有order $q=\#E({\mathbb{F}}_p)$，将${\mathbb{F}}_p$称为base field，${\mathbb{F}}_q$称为scalar field。

Halo2将instantiate proof system over the elliptic curve $E_p/{\mathbb{F}}_p$，需prove statements about ${\mathbb{F}}_q$-arithmetic circuit satisfiability。

QA：
curve为$E_p$ over ${\mathbb{F}}_p$，为何其arithmetic circuit为基于${\mathbb{F}}_q$而不是${\mathbb{F}}_p$的呢？
因为proof system通常是基于encodings of the scalars in the circuit（或更准确的说，commitments to polynomials whose coefficients are scalars）。这些scalars是基于${\mathbb{F}}_q$的，而其encodings或commitments则是elliptic curve point in $E_p/{\mathbb{F}}_p$。

但是，大多数Verifier的arithmetic computations是基于base field ${\mathbb{F}}_p$的，因此可高效表示为an ${\mathbb{F}}_p$-arithmetic circuit。

QA：
为何说Verifier的计算主要是基于${\mathbb{F}}_p$的呢？
因为Halo2中Verifier实际需使用circuit的output information来运行group operations。类似point doubling和point addition的group operations，都是arithmetic in ${\mathbb{F}}_p$，因为这些point的坐标值都是in ${\mathbb{F}}_p$的。

构建另一条scalar field为${\mathbb{F}}_p$曲线的主要目的是：【证明“Verifier的计算”为non-native arithmetic，借助cycles of curves，其对应为另一曲线 的native arithmetic。】

• 具有an ${\mathbb{F}}_p$-arithmetic circuit，可高效verify proofs from the first curve。
  此外，若第二条曲线的base field为$E_q/{\mathbb{F}}_q$，则将generate proofs that could be efficiently verified in the first curve’s ${\mathbb{F}}_q$-arithmetic circuit。换句话说，可instantiate a second proof system over $E_q{\mathbb{F}}_q$，从而形成a 2-cycle with the first：
  

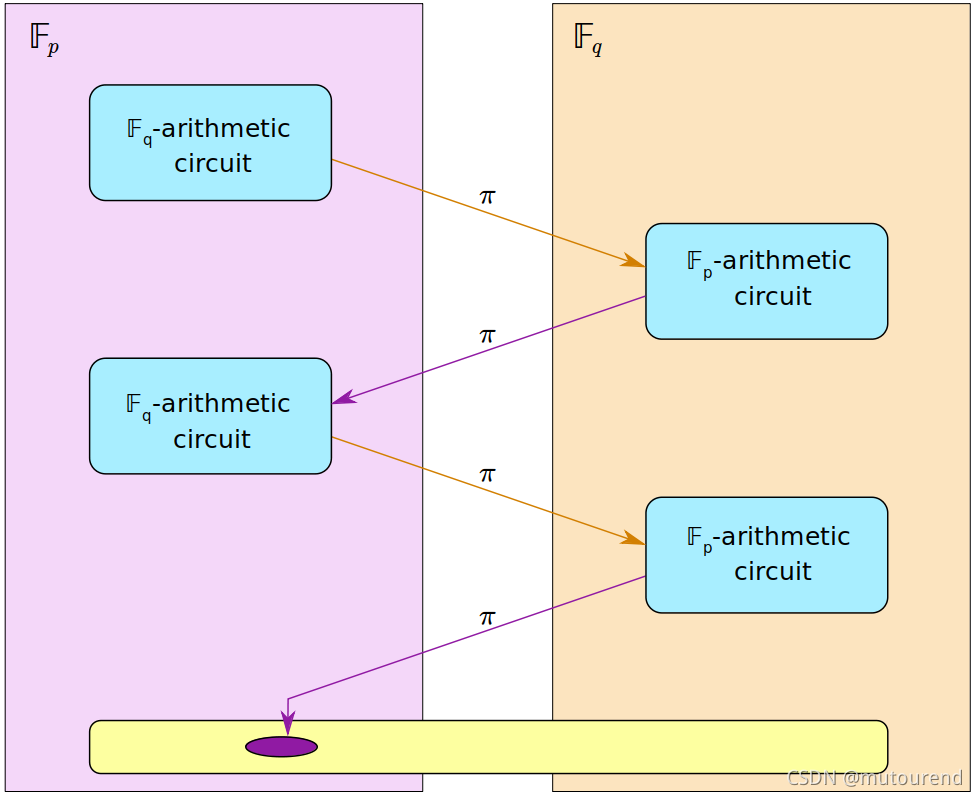
3. cycles of curves现状

当前知名的cycles of elliptic curves 有：

• 1）Secp_256k1/Secq_256k1。【详情见Spartan-ECDSA：最快的浏览器内 ZK secp256k1 ECDSA中的“附录：Secp256k1/Secq256k1曲线cycle”。】
• 2）FFT-friendly cycles of curves，如Pasta（Pallas/Vesta）。【详情见：Halo2学习笔记——背景资料之Elliptic curves（5） 和 Mina中的Pasta（Pallas和Vesta）曲线。】
• BN254/Grumpkin。【详细参数见Aztec Yellow Paper（包含了BN254 pairing和cycle曲线定义）。】

这些曲线的开源代码实现见：

• https://github.com/deevashwer/curves（Rust语言。实现了Pallas/Vesta、BN254/Grumpkin、Secp_256k1/Secq_256k1等曲线。）

当前cycles of curves在递归证明领域的应用现状为：

• 1）Mina基于Pasta（Pallas/Vesta）曲线构建递归证明。
• 2）ZCash Halo2基于Pasta（Pallas/Vesta）曲线构建递归证明。
• 3）微软Nova/SuperNova基于Pasta（Pallas/Vesta）曲线构建Folding scheme。
• 4）Spartan-ECDSA基于" Nova Folding scheme+Spartan+Secp_256k1/Secq_256k1曲线"构建 ECDSA group membership证明。
• 5）Aztec基于BN254/Grumpkin曲线构建Aztec 2.0（以太坊的多资产private rollup）。

但是，基于cycles of curves来构建约束系统，除带来复杂性问题（如需验证2个proof而不是1个proof）之外，还可能带来安全漏洞，以Nova/SuperNova为例：【详细见Nova早期代码实现中cycles of curves的攻击问题：David Wong博客 The zero-knowledge attack of the year might just have happened, or how Nova got broken】

4. cycles of curves并非必选项

为解决递归证明中，“证明验证proof”中的non-native arithmetic问题，在保证安全性的前提下并提升效率，有如下关键策略：

• 1）Lookup arguments：另一个减少non-native运算的重要策略为：引入基于foreign field椭圆曲线运算的大型lookup table。该方法将执行非原生椭圆曲线运算的问题转化为执行原生椭圆曲线运算，从而降低了任务的复杂性。

  • 如Aztec的Goblin Plonk方案：lazy recursive proof composition。

• 2）Weak prover-strong prover：该策略是在不泄露信息的情况下，将尽可能多的计算由 weak prover 推迟到给 stronger prover，从而最大限度地减少weak prover上的计算负载。即在weak机器上fold，在服务器端做non-native繁重计算。

• 3）Range checks：该方法只是简单地确保正在处理的数字不会超过scalar域的素数值。若将这些数字限制在一定范围内，可像使用整数一样使用它们。

• 4）Bignum techniques：在很多情况下，正在处理的数字确实会超过scalar域的素数值。这时可将这些数字切分为“limbs”，并对每个limb做range check验证。可做大量这样的range check，并使用相关技术来忽略“high limbs”。

  • 如zkSync的Franklin-crypto递归证明中采用的RNS算法。

• 5）Cycles of curves：

• 6）借助super-singular curves 或 其它椭圆曲线：如CPerezz19在(Intro to ZK Day) Elliptic Curve explorations - Catching up with Goldilocks & FRI 中提及的。
  Supersingular椭圆曲线的scalar field与base field相等，即${\mathbb{F}}_p={\mathbb{F}}_q$，即意味着，Supersingular椭圆曲线 cycle to 自身：

  • 不存在错误的域运算。
  • 可使用cycle的两端用于实际计算。

  但是embedding degree如果过低，会存在MOV攻击问题。如2005年Alfred Menezes An Introduction to Pairing-Based Cryptography论文中所指出：“自20世纪90年代初起，已达成共识，具有low embedding degree的elliptic curve不适合用于discrete log protocols中。但是，low embedding degree的elliptic curve在高效实现pairing-based protocols中至关重要。”
  

参考资料

[1] Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
[2] 基于cycle of curves的Nova证明系统（1）
[3] 基于cycle of curves的Nova证明系统（2）
[4] Cycles of curves: what are they and do we need them?
[5] Non-native field arithmetic with TurboPlonk, Plookup, etc
[6] Aztec emulated field and group operations
[7] The lookup singularity - how zero-knowledge proofs can be made simpler and easier to review
[8] Goblin Plonk：lazy recursive proof composition
[9] Accumulating IM transcripts across recursive proofs
[10] 大模数运算之中国余数定理 Modular Arithmetic CRT: How do modulo with very big numbers
[11] Aztec Yellow Paper（包含了BN254 pairing和cycle曲线定义）
[12] RNS（Residue number system）
[13] Halo2学习笔记——背景资料之Elliptic curves（5）