一、B-样条基函数
它有两条贝塞尔基函数所没有的特性,
(1)定义域被节点细分(subdivided);
(2) 基函数不是在整个区间非零。实际上,每个B样条基函数在附近一个子区间非零,
因此,B-样条基函数相当“局部”。
1.节点
设U 是m + 1个非递减数的集合,u0 <= u2 <= u3 <= ... <= um。ui称为节点(knots), 集合U 称为节点向量(knot vector), 半开区间[ui, ui+1) 是第i个节点区间(knot span)。
注意某些ui可能相等,某些节点区间会不存在。如果一个节点 ui 出现 k 次 (即,ui = ui+1 = ... = ui+k-1), 其中 k > 1, ui 是一个重复度(multiplicity)为k 的多重节点,写为 ui(k)。
否则,如果ui只出现一次,它是一个简单节点。如果节点等间距(即, ui+1 - ui 是一个常数,对 0 <= i <= m - 1),节点向量或节点序列称为均匀的;否则它是非均匀的。
节点可认为是分隔点,将区间[u0, um]细分为节点区间。所有B-样条基函数被假设定义域在[u0, um]上。在本文中,我们经常使用u0 = 0和um = 1,所以定义域是闭区间[0,1]。

二.三次B样条
B样条曲线分为近似拟合和插值拟合,
所谓近似拟合就是不过特征点,而插值拟合就是通过特征点,
但是插值拟合需要经过反算得到控制点再拟合出过特征点的B样条曲线方程。这里会一次介绍两种拟合算法。首先介绍B样条的曲线方程。
B样条曲线的总方程为:

其中P i 是控制曲线的特征点,Fi,k(u)则是K阶B样条基函数。
1.1 三次B样条曲线方程中基函数为:
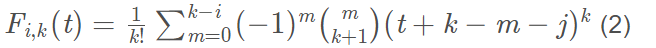
其中 表示阶乘。化成看的明白的式子就是(以四个控制点为例):
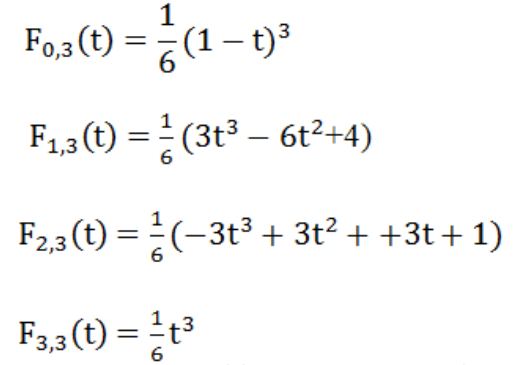
将图片上的基函数代入到方程(1)中,就是:

方程(3)就是三次B样条曲线方程。上式(2)的j是什么意思,其实j就是控制点的索引值。这里我把书上的公式摘抄下来,可能看起来更为清晰。参考书籍:《计算机图形学 第3版》何援军 第13章
三次B样条曲线计算
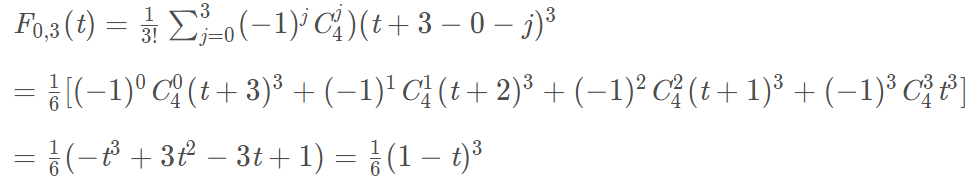

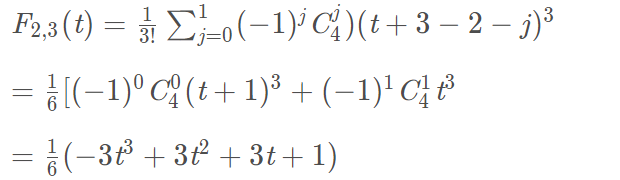
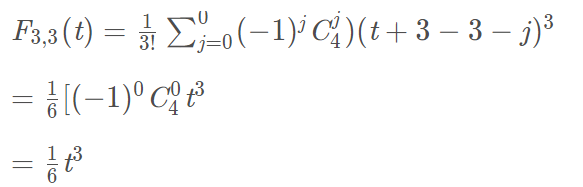
2 三次B样条曲线近似拟合
近似拟合很简单。不需要求控制点,求得
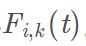
, 由上述方程(3),代入,就可以得到由这四个点近似拟合的一段三次B样条曲线,
起始点在P 0,终点在P 1,
对于闭合轮廓,最后一段可以取前两点做辅助,拟合实验结果我最后一块给出。这种近似拟合曲线光滑,但是最大不足就是不过特征点,也就是不过P i ,需要过点需要反求控制点再拟合。
3 三次B样条插值拟合
