B-Spline Curve

B-Spline Representation

Spline of degree $n$ as a spline of order $n+1$.

Let $a_{i}$ be a biinfinite and strictly increasing sequence of knots, which means $a_{i} \lt a_{i+1}$, for all $i$. We define the B-Splines $N_{i}^{n}$ with these knots by the recursion formula

$N_{i}^{n} = \begin{cases} 1 \hspace{1cm} for \ u \in [a_{i}, a_{i+1}) \\ 0 \hspace{1cm} otherwise \end{cases}$

and
$N_{i}^{n}(u) = \alpha_{i}^{n-1}N_{i}^{n-1}(u) + (1-\alpha_{i}^{n-1})N_{i+1}^{n-1}(u)$

where
$\alpha_{i}^{n-1} = \frac{u-a_{i}}{a_{i+n}-a_{i}}$

Graphical Representation of B-Splines

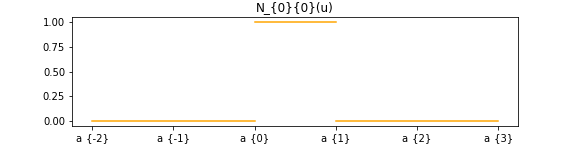
$N_{0}^{0}(u)$:

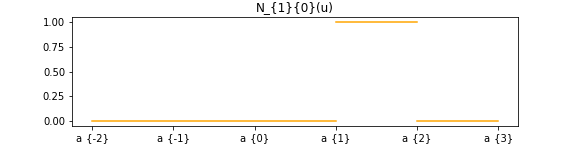
$N_{1}^{0}(u)$:
$N_{1}^{0}(u) = N_{0}^{0}(u-1)$

$N_{0}^{1}(u)$:
$\begin{aligned} N_{0}^{1}(u) &= \alpha_{0}^{0}N_{0}^{0}(u) + (1-\alpha_{1}^{0})N_{1}^{0}(u) \\ &= \frac{u-a_{0}}{a_{1}-a_{0}}N_{0}^{0}(u) + \frac{a_{2}-a_{1}-u+a_{1}}{a_{2}-a_{1}}N_{0}^{0}(u-1) \\ &= \frac{u-a_{0}}{a_{1}-a_{0}}N_{0}^{0}(u) + \frac{a_{2}-u}{a_{2}-a_{1}}N_{0}^{0}(u-1) \end{aligned}$

$N_{0}^{2}(u)$:
$\begin{aligned} N_{0}^{2}(u) &= \alpha_{0}^{1}N_{0}^{1}(u) + (1-\alpha_{1}^{1})N_{1}^{1}(u) \\ &= \frac{u-a_{0}}{a_{2}-a_{0}}N_{0}^{1}(u) + \frac{a_{3}-a_{1}-u+a_{1}}{a_{3}-a_{1}}N_{0}^{1}(u-1) \\ &= \frac{u-a_{0}}{a_{2}-a_{0}}N_{0}^{1}(u) + \frac{a_{3}-u}{a_{3}-a_{1}}N_{0}^{1}(u-1) \end{aligned}$

Properties of B-Splines

1. $N_{i}^{n}$ is piecewise polynomial of degree n.
2. $N_{i}^{n}(u)$ is piecewise polynomial of degree n.
3. $N_{i}^{n}(u)$ is positive in $(a_{i}, a_{i+n+1})$.
4. $N_{i}^{n}(u)$ is zero outside of $(a_{i}, a_{i+n+1})$.
5. $N_{i}^{n}(u)$ is right side continuous.
   

$N_{i}^{n}(u)$ 就是 $u \in (a_{i},a_{i+n+1})$区间内，值大于 $0$的 $n$次曲线； $u \notin (a_{i},a_{i+n+1})$时， $N_{i}^{n}(u) = 0$。

The De Boor algorithm

For $u \in [a_{n},a_{n+1})$:
$\begin{aligned} s(u) &= \sum_{i=0}^{n}c_{i}^{0}N_{i}^{n}(u) = \sum_{i=0}^{n}c_{i}^{0}[\alpha_{i}^{n-1}N_{i}{n-1}(u) + (1-\alpha_{i+1}^{n-1})N_{i+1}^{n-1}(u)] \\ &=c_{0}^{0}\alpha_{0}^{n-1}N_{0}^{n-1}(u) + c_{0}^{0}(1-\alpha_{1}^{n-1})N_{1}^{n-1}(u) + c_{1}^{0}\alpha_{1}^{n-1}N_{1}^{n-1}(u) + c_{1}^{0}(1-\alpha_{2}^{n-1})N_{2}^{n-1}(u) \\ &+ \dots \\ &+ c_{n-1}^{0}\alpha_{n-1}^{n-1}N_{n-1}^{n-1}(u) + c_{n-1}^{0}(1-\alpha_{n}^{n-1})N_{n}^{n-1}(u) + c_{n}^{0}\alpha_{n}^{n-1}N_{n}^{n-1}(u) + c_{n}^{0}(1-\alpha_{n+1}^{n-1})N_{n+1}^{n-1}(u) \end{aligned}$

Since $N_{0}^{n-1}(u) = 0$ and $N_{n+1}^{n-1}(u) = 0$, for $u \in [a_{n},a_{n+1})$. Thus:
$s(u) = \sum_{i=1}^{n}[c_{i-1}^{0}(1-\alpha_{i}^{n-1}) +c_{i}^{0}\alpha_{i}^{n-1}]N_{i}^{n-1}(u)$

Let $c_{i-1}^{0}(1-\alpha_{i}^{n-1}) +c_{i}^{0}\alpha_{i}^{n-1} = c_{i}^{1}$, then:
$\begin{aligned} s(u) &= \sum_{i=1}^{n}c_{i}^{1}N_{i}^{n-1}(u) \\ &= \sum_{i=2}^{n}c_{i}^{2}N_{i}^{n-2}(u) \\ &\dots \\ &= \sum_{i=n-1}^{n}c_{i}^{n-1}N_{i}^{1}(u) \\ &= \sum_{i=n}^{n}c_{i}^{n}N_{i}^{0}(u) \\ &= c_{n}^{n} \end{aligned}$
即（参考De Casteljau Algorithm）：
$\begin{aligned} for \ i \in \{1,\dots,n\} \hspace{1cm} &c_{i}^{1} = c_{i-1}^{0}(1-\alpha_{i}^{n-1}) + c_{i}^{0}\alpha_{i}^{n-1} \\ for \ i \in \{2,\dots,n\} \hspace{1cm} &c_{i}^{2} = c_{i-1}^{1}(1-\alpha_{i}^{n-2}) + c_{i}^{1}\alpha_{i}^{n-2} \hspace{1cm} \\ &\dots \\ for \ i \in \{n-1,n\} \hspace{1cm} &c_{i}^{n-1} = c_{i-1}^{n-2}(1-\alpha_{i}^{1}) + c_{i}^{n-2}\alpha_{i}^{1} \\ for \ i \in \{n\} \hspace{1cm} &c_{i}^{n} = c_{i-1}^{n-1}(1-\alpha_{i}^{0}) + c_{i}^{n-1}\alpha_{i}^{0} \\ \end{aligned}$

对于 $u \in [a_{n},a_{n+1})$，如果Control Points $c_{i}^{0} = 1$，且每层 $\alpha_{i}$均等于 $\alpha$，则：
$\begin{aligned} s(u) &= \sum_{i=0}^{n}c_{i}^{0}N_{i}^{n}(u) \\ &= c_{n}^{n} = \sum_{i=0}^{0}\lgroup_{i}^{0} \rgroup c_{n-i}^{n}(1-\alpha)^{i} \alpha^{0-i} \\ &= c_{n-1}^{n-1}(1-\alpha) + c_{n}^{n-1}\alpha = \sum_{i=0}^{1}\lgroup_{i}^{1} \rgroup c_{n-i}^{n-1}(1-\alpha)^{i} \alpha^{1-i} \\ &= c_{n-2}^{n-2}(1-\alpha)^{2} + 2c_{n-1}^{n-2}(1-\alpha)\alpha + c_{n}^{n-2}\alpha^{2} = \sum_{i=0}^{2}\lgroup_{i}^{2} \rgroup c_{n-i}^{n-2}(1-\alpha)^{i} \alpha^{2-i} \\ &= c_{n-3}^{n-3}(1-\alpha)^{3} + 3c_{n-2}^{n-3}(1-\alpha)^{2}\alpha + 3c_{n-1}^{n-3}(1-\alpha)\alpha^{2} + c_{n}^{n-3}\alpha^{3} = \sum_{i=0}^{3}\lgroup_{i}^{3} \rgroup c_{n-i}^{n-3}(1-\alpha)^{i} \alpha^{3-i} \\ &\dots \\ &= \sum_{i=0}^{n} \lgroup_{i}^{n}c_{n-i}^{0}(1-\alpha)^{i}\alpha^{n-i} = [(1-\alpha) + \alpha]^{n} = 1 \end{aligned}$

Thus, B-Splines $N_{i}^{n}(u)$ form the partition of unity, for $u \in [a_{n},a_{n+1})$.

对于 $s(u), n=3$： $s(u)$在 $u \in [a_{n},a_{n+1})$区间内就是一个Bezier Curve（以 $c_{0}^{0}$， $c_{1}^{0}$， $c_{2}^{0}$和 $c_{3}^{0}$为Control Points）。

B-Spline Properpties

1. The B-Splines of degree $n$ with a given knot sequence that do not varnish over some knot interval are linearly independent over this interval.

2. Adimension count shows that the B-Splines $N_{0}^{n}, \dots, N_{m}^{n}$ with the knots $a_{0}, \dots, a_{m+n+1}$ form a basis for all splines of degree $n$ with support $[a_{0}, a_{m+n+1}]$ and the same knots.

3. Similarly, the B-Splines $N_{0}^{n}, \dots, N_{m}{n}$ over the knots $a_{0}, \dots, a_{m+n+1}$ restricted to the interval $[a_{0}, a_{m+n+1}]$ form a basis for all splines of degree $n$ restricted to the same interval.

4. The B-Splines of degree $n$ form a partition of unity , i.e.,

$\sum_{i=0}^{m} = N_{i}^{n}(u) = 1 \hspace{1cm} for \ u \in [a_{n}, a_{m+1})$

5. A spline $s[a_{n}, a_{m+1})$ of degree $n$ with n-fold end knots,

$(a_{0} =) a_{1} = \dots = a_{n} \hspace{1cm} and \hspace{1cm} a_{m+1} = \dots = a_{m+n} (= a_{m+n+1})$

have the same end points and end tangents as its control polygon.

6. The end knots $a_{0}$ and $a_{m+n+1}$ have no influences on $N_{0}^{n}$ and $N_{m}^{n}$ over the interval $[a_{n}, a_{m+1})$.
7. The B-Splines are postive over the interior of the support,

$N_{i}^{n}(u) \gt 0 \hspace{1cm} for \ u \in(a_{i}, a_{i+n+1})$

8. The B-Splines have compact support,

$Supp\ N_{i}^{n} = [a_{i}, a_{i+n+1}]$

9. The B-Splines satisfy the de Boor, Mansfield, Cox recursion formula

$N_{i}^{n}(u) = \alpha_{i}^{n-1}N_{i}^{n-1}(u) + (1-\alpha_{i+1}^{n-1})N_{i+1}^{n-1}(u)$

where $\alpha_{i}^{n-1} = \frac{u-a_{i}}{a_{n+1}-a_{i}}$ represents the local parameter over the support of $N_{i}^{n-1}$.

10. The derivative of a single B-Spline is given by

$\frac{d}{du}N_{i}^{n}(u) = \frac{n}{u_{i+n}-u_{i}}N_{i}^{n-1}(u) - \frac{n}{u_{i+n+1}-u_{i+1}}N_{i+1}^{n-1}(u)$

11. The B-Spline representation of a spline curve is invariant under affine maps.
12. Any segment $s_{j}[a_{j},a_{j+1}]$ of an n-th degree spline lines in the convex hull of its $n+1$ control point $c_{j-n}, \dots, c_{j}$.

Conversion to B-Spline form

Since any polynomial of degree $n$ can be viewed as spline of degree $n$ or high with an arbitrary sequence of knots, one can express the monomials as linear combinations of B-Splines over any knot sequence ( $a_{i}$).