三大保边滤波算法:引导滤波、双边滤波、加权最小二乘平滑滤波算法
双边滤波
各向异性滤波,基于小波变换的滤波(Edge-avoiding wavelets and their applications),基于域变换的滤波(Domain Transform for Edge-Aware Image and Video Processing),基于geodesic的滤波(Geodesic Image and Video Editing)
双边滤波器:非线性滤波器,输出图像每个像素都是其邻域各像素的加权平均,权值随空间距离和数值差异的增加而减小。
B L F ( g ) p = 1 k p ∑ q G σ s ( ∣ ∣ p − q ) G σ r ( ∣ ∣ g p − g q ) BLF(g)_p=\frac{1}{k_p}\sum_q G_{\sigma_s}(||p-q)G_{\sigma_r}(||g_p-g_q) BLF(g)p=kp1q∑Gσs(∣∣p−q)Gσr(∣∣gp−gq)
k p = ∑ q G σ s ( ∣ ∣ p − q ∣ ∣ ) G σ r ( ∣ ∣ g p − g q ∣ ∣ ) k_p=\sum_q G_{\sigma_s}(||p-q||)G_{\sigma_r}(||g_p-g_q||) kp=q∑Gσs(∣∣p−q∣∣)Gσr(∣∣gp−gq∣∣)
其中,g为输入图像,p和q表示像素的空间位置,核函数 G σ s G_{σ_s } Gσs、 G σ r G_{σ_r } Gσr通常高斯核, σ s σ_s σs决定空间支撑、 σ r σ_r σr决定值域支撑调节边缘敏感度
双边滤波器性能定性分析:
1.给定像素p,其原始像素值为 g p g_p gp (a particular pixel p, whose unfiltered value is g p g_p gp )。随 σ s σ_s σs的增大,更多的邻域像素q参与像素p的平滑,其中与 g p g_p gp相近的 g q g_q gq 贡献最大,导致平滑后p点像素值与g_p差值很小(as σ s σ_s σs is increased, more and more distant pixels q , whose value g q g_q gq is close to g p g_p gp are being averaged together, and as a result the filtered value does not stray too far from g p g_p gp )。当 σ s → ∞ σ_s→ ∞ σs→∞时,双边滤波器等同于值域滤波器(in the limit ( σ s → ∞ σ_s → ∞ σs→∞), the bilateral filter becomes a range filter)。因此,为实现大尺度平滑,不仅需要增大 σ s σ_s σs, σ r σ_r σr也需要相应增加(more aggressive smoothing cannot be achieved only by increasing σ s σ_s σs , and the range support σ r σ_r σr must be increased as well)。
2.增大 σ r σ_r σr会降低双边滤波器的保边性能,导致部分边缘模糊(increasing σ_r reduces the ability of the bilateral filter to preserve edges, and some of them become blurred)。当 σ r → ∞ σ_r → ∞ σr→∞,双边滤波器等同于高斯滤波器(in the limit ( σ r → ∞ σ_r → ∞ σr→∞ ) the bilateral filter becomes a linear Gaussian filter)。
imgfilter = cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace,borderType)
# 使用方法
imgfilter = cv2.bilateralFilter(img, 11, 25, 25)
第一个参数src,表示输入图像
第二个参数d,表示在滤波过程中每个像素邻域的直径
第三个参数sigmaColor,颜色空间滤波器的sigma值。这个值越大,表示该像素领域内有更宽的颜色被混合到一起
第四个参数sigmaSpace,坐标空间中滤波器的sigma值,值越大,表示更大的区域足够相似的颜色获取相同的颜色。当d>0时,无论sigmaSpace取何值,d指定邻域大小。否则d正比与sigmaSpace。
第五个参数borderType,处理边界模式,可直接选默认值

导数滤波
文章链接:链接1
有博主做了翻译:链接2
引导滤波的定义中,用到了局部线性模型,该模型认为某函数上一点与其邻近部分的点成线性关系,一个复杂的函数可以用多个局部的线性函数来表示,当需求该函数上某一点的值时,只需计算所有包含该点的线性函数的值做平均,引导滤波函数的输入输出在二维窗口内满足线性关系:
q i = a k I i + b k , ∀ i ∈ w k q_i=a_k I_i+b_k,∀i∈w_k qi=akIi+bk,∀i∈wk
p是输入图像,I是引导图像,q是滤波输出图像, a k a_k ak和 b k b_k bk是系数, w k w_k wk是窗口
对等式两边求导 ∇ q = a ∇ I ∇q=a∇I ∇q=a∇I
当引导图像 I I I有梯度时,输出q也有类似的梯度
最小化输出图q和输入图p的差别,定义代价函数:
E ( a k , b k ) = ∑ i ∈ w k ( ( a k I i + b k − p i ) 2 + ϵ a k 2 ) E(a_k,b_k )=\sum_{i∈w_k}((a_k I_i+b_k-p_i )^2+ϵa_k^2) E(ak,bk)=i∈wk∑((akIi+bk−pi)2+ϵak2)
这里,ϵ是正则化参数,对代价函数求最小值
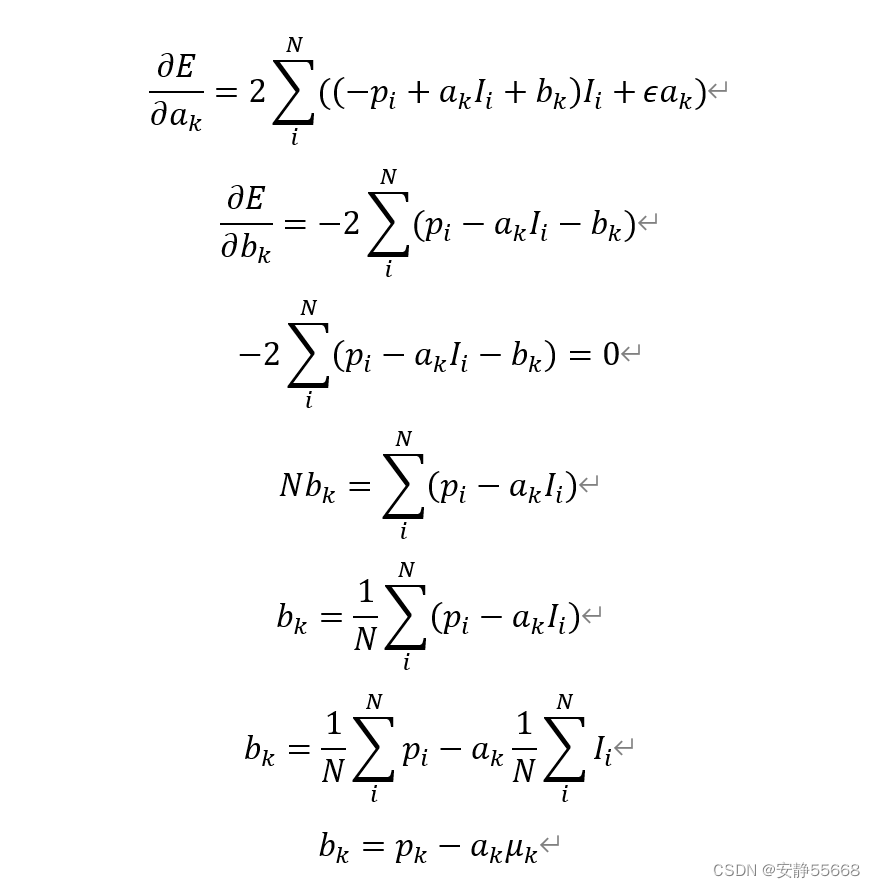
p k p_k pk和 μ k μ_k μk是p和I窗口内的均值。求 a k a_k ak
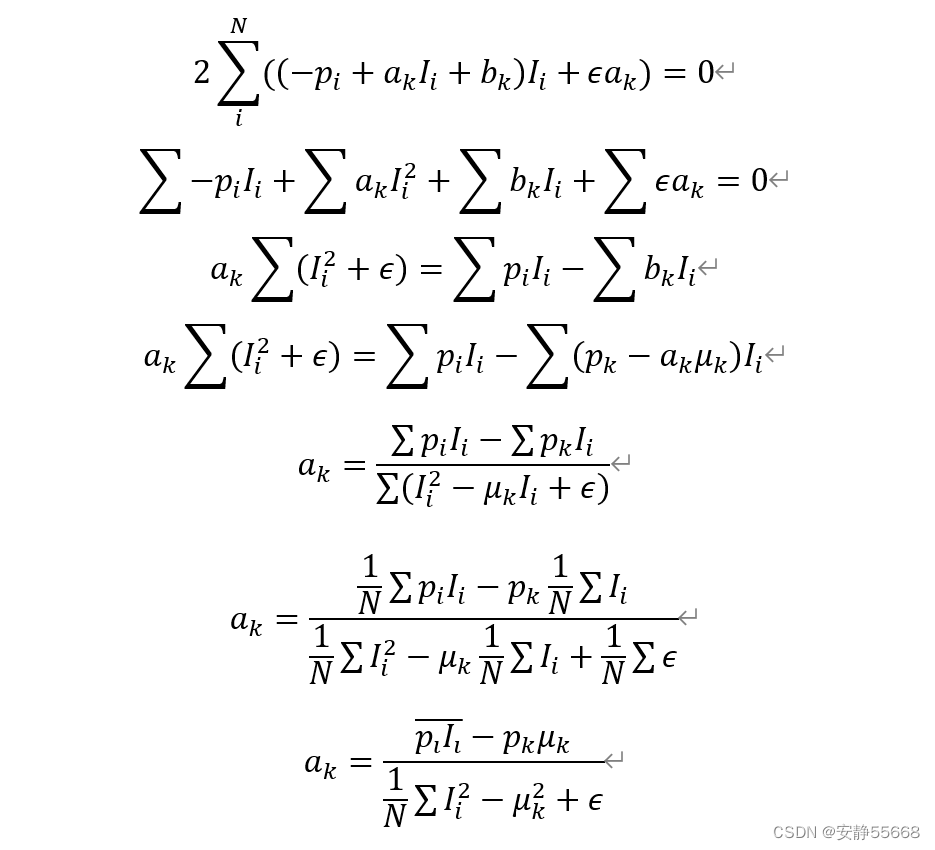
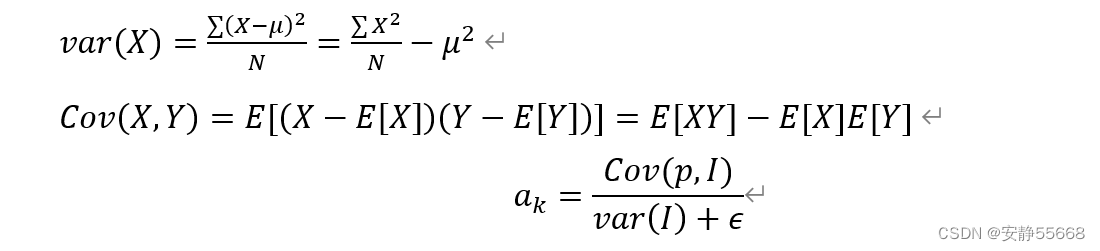
当作为滤波器时,通常I=p,
如果 ϵ = 0 ϵ=0 ϵ=0,从上式中可以看出,滤波器没有任何作用,输出等于输入
ϵ > 0 ϵ>0 ϵ>0,在像素强度变化小的区域,做了一个加权均值滤波,在变化大的区域,对图像的滤波效果很弱,有助于保持边缘
ϵ ϵ ϵ的作用就是界定变化的大小,在窗口不变的情况下,随着ϵ的增大,滤波效果更加明显。
指导滤波算法流程:

以彩色图像做指导滤波
上面的结果,图像对应位置相乘,都是单通道的情况,指导图为单通道,如果要用彩色图像为指导图,则略微复杂一点

import cv2
import numpy as np
from skimage.metrics import peak_signal_noise_ratio
def guide_filter(I, p, r, eps):
"""
:param I: 引导图像
:param p: 输入图像
:param r: 窗口半径
:param eps:
:return:
"""
I = I / 255 # 引导滤波图像必须归一化
p = p / 255
winSize = (2 * r + 1, 2 * r + 1)
# I的均值
mean_I = cv2.blur(I, winSize)
# p的均值
mean_p = cv2.blur(p, winSize)
# I*I和I*p的均值平滑
mean_II = cv2.blur(I*I, winSize)
mean_Ip = cv2.blur(I*p, winSize)
# 方差
var_I = mean_II - mean_I * mean_I
# 协方差
cov_Ip = mean_Ip - mean_I * mean_p
a = cov_Ip / (var_I + eps)
b = mean_p - a*mean_I
# 对a、b进行均值平滑
mean_a = cv2.blur(a, winSize)
mean_b = cv2.blur(b, winSize)
q = mean_a * I + mean_b
q = q * 255
q[q > 255] = 255
return q.astype(np.uint8)
if __name__ == '__main__':
img = cv2.imread('1.jpg', 0)
# 引导滤波
imgguidefilter = guide_filter(img, img, 16, 1e-2)
cv2.imshow('img', img)
cv2.imshow('guide_filter', imgguidefilter)
cv2.waitKey()

加权最小二乘法滤波原理
链接1
基于双边滤波的算法无法在多尺度提取到很好的细节信息,并可能出现伪影。加权最小二乘滤波目的即是使得结果图像u与原图像p经过平滑后尽量相似,但是在边缘部分尽量维持原状
∑ p ( ( u p − g p ) 2 + λ ( a x , p ( g ) ( ∂ u ∂ x ) p 2 + a y , p ( g ) ( ∂ u ∂ y ) p 2 ) \sum_p ((u_p-g_p)^2+\lambda(a_{x,p}(g)(\frac{\partial_u}{\partial_x})_p^2+a_{y,p}(g)(\frac{\partial_u}{\partial_y})_p^2) ∑p((up−gp)2+λ(ax,p(g)(∂x∂u)p2+ay,p(g)(∂y∂u)p2) 式(1)
其中 a x a_x ax, a y a_y ay为权重系数。目标函数第一项代表输入图像和输出图像越相似越好;第二项是正则项,通过最小化的偏导,使得输出图像越平滑越好,上式可以改写为矩阵形式:
( u − g ) T ( u − g ) + λ ( u T D x T A x D x u + u T D y T A y D y u ) (u-g)^T (u-g)+λ(u^T D_x^T A_x D_x u+u^T D_y^T A_y D_y u) (u−g)T(u−g)+λ(uTDxTAxDxu+uTDyTAyDyu) 式(2)
其中, A x A_x Ax, A y A_y Ay为以 a x a_x ax, a y a_y ay为对角元素的对角矩阵, D x D_x Dx, D y D_y Dy为前向差分矩阵,和是后向差分算子,使得上式最小值,u满足:
( I + λ L g ) u = g (I+λL_g )u=g (I+λLg)u=g 式(3)
(
注:式3推导,式2对u求导,导数为0。 u T u = u 2 u^T u=u^2 uTu=u2
∂ ( ( u − g ) 2 + λ ( u 2 D x T A x D x + u 2 D y T A y D y ) ) ∂ u = 0 \frac{∂((u-g)^2+λ(u^2 D_x^T A_x D_x+u^2 D_y^T A_y D_y ))}{∂u}=0 ∂u∂((u−g)2+λ(u2DxTAxDx+u2DyTAyDy))=0
2 ( u − g ) + 2 λ u ( D x T A x D x + D y T A y D y ) = 0 2(u-g)+2λu(D_x^T A_x D_x+D_y^T A_y D_y )=0 2(u−g)+2λu(DxTAxDx+DyTAyDy)=0
u ( I + λ ( D x T A x D x + D y T A y D y ) ) = g u(I+λ(D_x^T A_x D_x+D_y^T A_y D_y ))=g u(I+λ(DxTAxDx+DyTAyDy))=g
)
其中, L g = D x T A x D x + D y T A y D y L_g=D_x^T A_x D_x+D_y^T A_y D_y Lg=DxTAxDx+DyTAyDy,作者取的平滑权重系数为
a x , p ( g ) = ( ∣ ∂ l ∂ x ( p ) ∣ α + ε ) − 1 , a y , p ( g ) = ( ∣ ∂ l ∂ y ( p ) ∣ α + ε ) − 1 a_{x,p} (g)=(|\frac{∂l}{∂x} (p)|^α+ε)^{-1}, a_{y,p} (g)=(|\frac{∂l}{∂y }(p)|^α+ε)^{-1} ax,p(g)=(∣∂x∂l(p)∣α+ε)−1,ay,p(g)=(∣∂y∂l(p)∣α+ε)−1
其中I表示Log,ε一般取0.0001,式3求出u为:
u = F λ ( g ) = ( I + λ L g ) − 1 g u=F_λ (g)=(I+λL_g )^{-1} g u=Fλ(g)=(I+λLg)−1g
当所选区域连续,平滑权重系数可以近似为a_x≈a_y≈a,那么
F λ ( g ) ≈ ( I + λ L g ) − 1 g F_λ (g)≈(I+λL_g )^{-1} g Fλ(g)≈(I+λLg)−1g
L为拉普拉斯齐次矩阵
注:拉普拉斯矩阵
拉普拉斯矩阵(Laplacian matrix) 也叫做导纳矩阵、基尔霍夫矩阵或离散拉普拉斯算子,是图论中用于表示图的一种重要矩阵。
定义:给定一个具有n个顶点的简单图G=(V,E),V为顶点集合,E为边集合,其拉普拉斯矩阵可定义为:
L = D − A L=D-A L=D−A
其中A∈R为邻接矩阵, D ∈ R n × n D∈R^{n×n} D∈Rn×n为度矩阵
(邻接矩阵是表示顶点之间相邻关系的矩阵。
A i j = { w i j , ( v i , v j ) 或 < v i , v j > ∈ E ( G ) 0 或 ∞ , ( v i , v j ) 或 < v i , v j > ∉ E ( G ) A_ij=\left\{ \begin{array}{ll} w_{ij} &, (v_i,v_j )或<v_i,v_j>∈E(G)\\ 0或\infty &,(v_i,v_j )或<v_i,v_j>∉E(G) \end{array} \right. Aij={ wij0或∞,(vi,vj)或<vi,vj>∈E(G),(vi,vj)或<vi,vj>∈/E(G)
w i j w_ij wij表示边上的权重, E ( G ) E(G) E(G)边的集合)
注意A中的元素仅仅可能是0和1,且其对角元素全为0。D是一个对角矩阵,其对角线上的元素计算方式 D i i = ∑ j A i j D_{ii}=\sum_j A_{ij} Dii=∑jAij 。L的每个元素值的具体计算方式如下:
L i j = { D i j i f i = j − 1 i f i ≠ j a n d v i i s a d j a c e n t t o v j 0 o t h e r w i s e L_{ij}=\left\{ \begin{array}{ll} D_{ij} &if i=j \\ -1&if i\ne j and v_i is adjacent to v_j \\ 0 & otherwise \end{array} \right. Lij=⎩
⎨
⎧Dij−10ifi=jifi=jandviisadjacenttovjotherwise
拉普拉斯矩阵都是对称的
