1、相机标定原理

---

   相机标定可以说是计算机视觉/机器视觉的基础，也是面试过程中经常出现的问题。相机标定涉及的知识面很广，成像几何、镜头畸变、单应矩阵、非线性优化等。在双目测距系统中，相机标定能消除畸变，进行立体校正，从而提高视差计算的准确性，这样才能得到精确的深度图。

1、相机模型

1.1 各个坐标系

  确定空间某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型（各个坐标系），这些坐标系之间的转换参数就是相机参数，求解参数的过程叫做相机标定（摄像机标定）。建立立体视觉系统所需要的各个坐标系，包括世界坐标系、相机坐标系、以及图像坐标系（物理和像素坐标系）。

坐标系名称	坐标系描述
世界坐标系（3D）	描述目标在真实世界中的位置引入的参考坐标系(Xw，Yw，Zw)
相机坐标系（3D）	联系世界坐标系与图像坐标系的桥梁，一般取摄像机的光学轴为ｚ轴(Xc，Yc，Zc)
图像物理坐标系（2D）	根据投影关系引入，方便进一步得到像素坐标，单位为毫米，坐标原点为摄像机光轴与图像物理坐标系的交点位置(x，y)
图像像素坐标系（2D）	真正从相机内读到的信息，图像物理坐标的离散化，以像素为单位，坐标原点在左上角(u,v)

首先明确各个坐标系之间的转换关系：

1.世界坐标系与相机坐标系

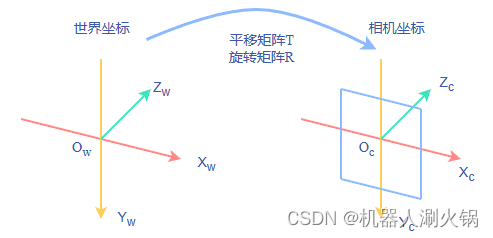
  这是将一个三维的坐标系(X_w，Y_w，Z_w) 转换成另一个三维的坐标系(X_c，Y_c，Z_c)，这两个坐标系之间的转换属于刚体转换，物体只改变在两个坐标系中的空间位置(平移)和朝向(旋转),而不改变其形状。它们之间的转换关系可以用旋转矩阵Ｒ和平移矩阵Ｔ来完成，这两个矩阵反映了世界坐标系与相机坐标系之间的转换关系，合称外参矩阵L_w。获得了外参矩阵，这样已知世界坐标系中的一点通过转换关系就可以得到此点在相机坐标系的位置，反之亦成立。

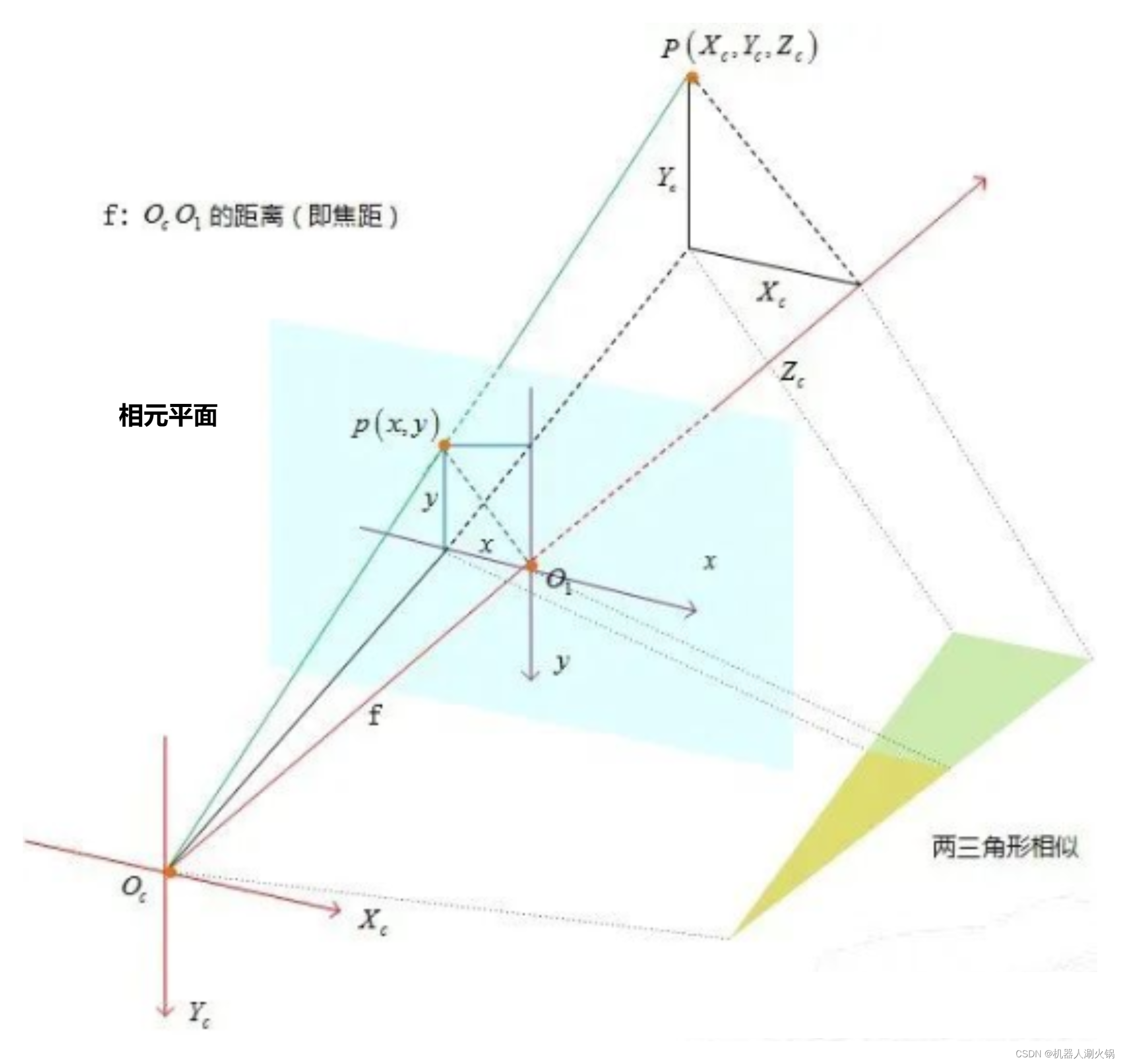
2.相机坐标系与图像物理坐标系

  这是一个将三维的坐标系转化为二维的坐标系，这两个坐标系之间的转换要通过几何投影模型关系获得，下面是两个坐标系的投影关系示意图：

3.图像物理坐标系与图像像素坐标系

   首先以一个形象的例子来说明两个坐标系间的区别。物理坐标系是一个连续的概念，它是以毫米为单位，就好比某一观众在电影院里的具体坐标值(3.4，5.9)；而像素坐标系是一个离散的概念，它是以像素作为单位，只能是整数值坐标，就好比某一观众在电影院里的位置是(第三排，第六列)。另外还需要注意的是，这两个坐标系的原点位置也不相同，物理坐标系将原点定为摄像机光轴与图像物理坐标系的交点位置，通常称其为主点；而像素坐标系则以像素图像的左上角为原点。

世界坐标系转换为像素坐标系

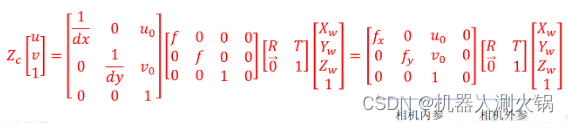
   其中 f 为摄像机的焦距，单位一般是mm；d_x，d_y 为像元尺寸;u₀,V₀为图像中心。f_x = f/d_x, f_y = f/d_y,分别称为x轴和y轴上的归一化焦距。

1.2 相机畸变模型

一般只考虑径向畸变k和切向畸变p
$$\begin{array}{c}{x}_{distorted}=x\ast (1+k_1{r}^2+k_2{\gamma }^4+k_3{\gamma }^6)+2p_{1}xy+p_2({\gamma }^2+2x^2)\\ y_{distorted}=y\ast (1+k_1{r}^2+k_2{\gamma }^4+k_3{\gamma }^6)+2p_{1}xy+p_2({\gamma }^2+2y^2)\end{array}$$
其中${\gamma }^2=x^2+y^2$。
   一般选择2或3个k值，这个是经验证过可以获得较好的结果，如果k取得再多影响不会很大可以忽略，甚至可能反而导致效果不好。

畸变模型：枕型畸变(k>0)和桶型畸变(k<0)

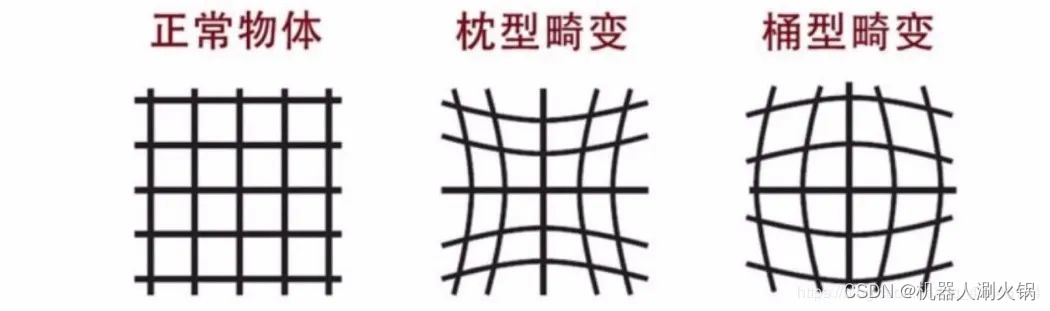
当k>0时，r越大（点离中心越远），畸变量越大，r越小，畸变量越小，呈枕型。

当k<0时，r越大（点离中心越远），畸变量越小，r越小，畸变量越大，呈桶型。

1.3 相机标定参数

内参：

（单位长度的像素个数）f_x、f_y

（主点坐标）c_x、c_y

（畸变系数）k₁、k₂、k₃、p₁、p₂

外参：
（旋转和平移矩阵）R、T

2、张友正标定法

   张正友标定法利用如下图所示的棋盘格标定板，在得到一张标定板的图像之后，可以利用相应的图像检测算法得到每一个角点的像素坐标(u,v) 。

   张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 W=0，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标(U,V,W=0)。

   利用这些信息：每一个角点的像素坐标(u,v) 、每一个角点在世界坐标系下的物理坐标(U,V,W=0)，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

张正友标定法标定相机的内外参数的思路如下：

1）、求解内参矩阵与外参矩阵的积；

2）、求解内参矩阵；

3）、求解外参矩阵。

2.1 求解内参矩阵与外参矩阵的积

  将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标W=0 ，因此，原单点无畸变的成像模型可以化为下式。其中，R1,R2 为旋转矩阵R 的前两列。为了简便，将内参矩阵记为A 。

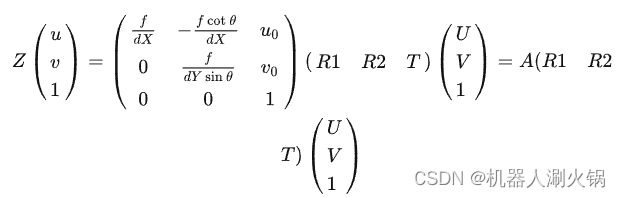
   我们对于上式做一定的说明。对于不同的图片，内参矩阵A 为定值；对于同一张图片，内参矩阵A，外参矩阵(R₁ R₂ T) 为定值；对于同一张图片上的单点，内参矩阵A，外参矩阵(R₁ R₂ T)，尺度因子 Z 为定值。

   我们将A(R₁ R₂ T) 记为矩阵H ，H 即为内参矩阵和外参矩阵的积，记矩阵 H 的三列为 (H₁,H₂,H₃) ，则有：

利用上式，消去尺度因子Z，可得：

   此时，尺度因子Z已经被消去，因此上式对于同一张图片上所有的角点均成立。(u,v) 是像素坐标系下的标定板角点的坐标，(U,V) 是世界坐标系下的标定板角点的坐标。通过图像识别算法，我们可以得到标定板角点的像素坐标 (u,v)，又由于标定板的世界坐标系是人为定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到世界坐标系下的 (U,V)。

   由于这里的 H 是齐次矩阵，有8个独立未知元素。每一个标定板角点可以提供两个约束方程（u,U,V 的对应关系、v,U,V 的对应关系提供了两个约束方程），因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵 H 。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵 H。

2.2 求解内参矩阵

   我们已知了矩阵H=A(R₁ R₂ T)，接下来需要求解相机的内参矩阵A 。我们利用R1,R2作为旋转矩阵 R 的两列，存在单位正交的关系，即：
$$\begin{array}{c}{R}_1^{T}R2=0\\ R_1^T{R}_1=R_2^T{R}_2=1\end{array}$$
则由 H 和 R₁，R₂ 的关系，可知：
$$\begin{array}{c}{R}_1=A^{-1}{H}_1\\ R_2=A^{-1}{H}_2\end{array}$$
代入可得：
$$\begin{array}{c}{H}_1^T{A}^{-T}{A}^{-1}{H}_2=0\\ H_1^T{A}^{-T}{A}^{-1}{H}_1=H_2^T{A}^{-T}{A}^{-1}{H}_2=1\end{array}$$
   另外，我们发现，上述两个约束方程中均存在矩阵A^−T A⁻¹ 。因此，我们记A^−T A⁻¹=B ，则 B为对称阵。我们试图先求解出矩阵 B ，通过矩阵 B 再求解相机的内参矩阵 A 。

同时，为了简便，我们记相机内参矩阵 A 为：

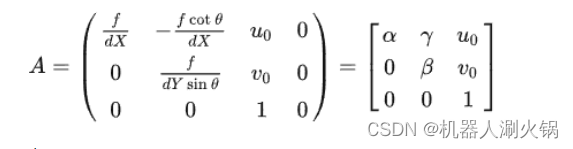
则：

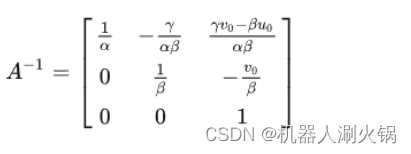
则用矩阵 A表示矩阵 B 得：

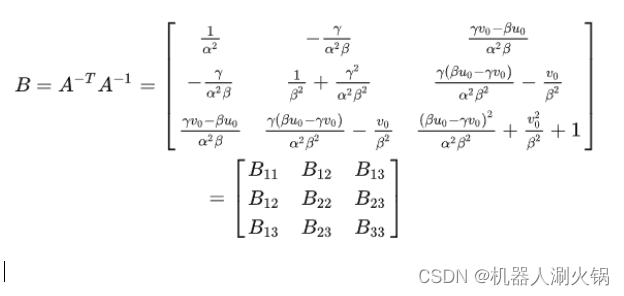
注意：由于 B 为对称阵，上式出现了两次B₁₂,B₁₃,B₂₃ 。

这里，我们可以使用B=A^−T A⁻¹ 将前面通过R1,R2 单位正交得到的约束方程化为：

H1 ^TBH2 = 0 H1 ^TBH1 = H2 ^TBH2 = 1 因此，为了求解矩阵 B ，我们必须计算H ^_iTB H _j 。则：

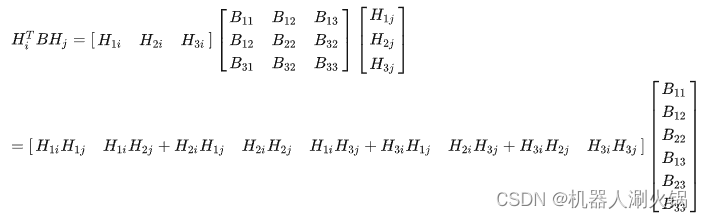
上述方程看起来有点复杂，但是其实不然，我们可以记：

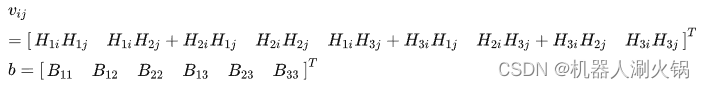
则上述方程化为：H_i^TBH_j = v_ijb
此时，通过 R1,R2 单位正交得到的约束方程可化为：
$$\begin{array}{c}{v}_{12}^{T}b=0\\ v_{11}^{T}b=v_{22}^{T}b=1\end{array}$$
即：
$$\left[\begin{array}{c}{v}_{12}^T\\ v_{11}^T-v_{22}^T\end{array}\right]b=vb=0$$
其中，矩阵
$$v=\left[\begin{array}{c}{v}_{12}^T\\ v_{11}^T-v_{22}^T\end{array}\right]$$
由于矩阵 H 已知，矩阵 v 又全部由矩阵 H 的元素构成，因此矩阵 v 已知。

   此时，我们只要求解出向量 b ，即可得到矩阵 B 。每张标定板图片可以提供一个vb=0 的约束关系，该约束关系含有两个约束方程。但是，向量 b 有6个未知元素。因此，单张图片提供的两个约束方程是不足以解出来向量 b。因此，我们只要取3张标定板照片，得到3个 vb=0 的约束关系，即6个方程，即可求解向量 b。当标定板图片的个数大于3时（事实上一般需要15到20张标定板图片），可采用最小二乘拟合最佳的向量 b ，并得到矩阵 B。

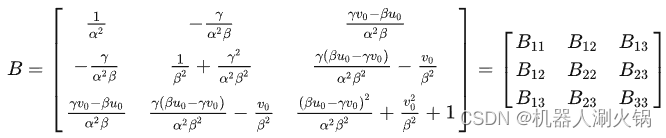
根据矩阵 B 的元素和相机内参 α, β, γ, u0, v0 的对应关系（如上式），可得到：

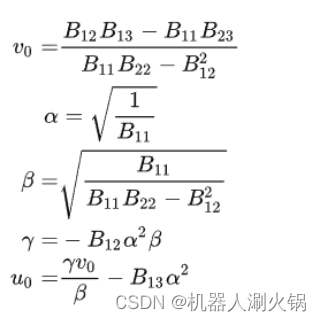
即可求得相机的内参矩阵

2.3 求解外参矩阵

   这里再次强调一下，对于同一个相机，相机的内参矩阵取决于相机的内部参数，无论标定板和相机的位置关系是怎么样的，相机的内参矩阵不变。这也正是在第2部分“求解内参矩阵”中，我们可以利用不同的图片（标定板和相机位置关系不同）获取的矩阵 H ，共同求解相机内参矩阵 A 的原因。

   但是，外参矩阵反映的是标定板和相机的位置关系。对于不同的图片，标定板和相机的位置关系已经改变，此时每一张图片对应的外参矩阵都是不同的。

   在关系：A(R1 R2 T)=H 中，我们已经求解得到了矩阵 H （对于同一张图片相同，对于不同的图片不同）、矩阵 A （对于不同的图片都相同）。通过公式：(R1 R2 T)=A⁻¹ H ，即可求得每一张图片对应的外参矩阵 (R1 R2 T) 。

   注意，这里值得指出，完整的外参矩阵为：
$$\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$$
但是，由于张正友标定板将世界坐标系的原点选取在棋盘格上，则棋盘格上任一点的物理坐标 W=0，将旋转矩阵的 R 的第三列 R3 消掉，因此，R3 在坐标转化中并没有作用。但是 R3 要使得 R 满足旋转矩阵的性质，即列与列之间单位正交，因此可以通过向量 R1,R2 的叉乘，即 R3=R1×R2 ，计算得到 R3。

此时，相机的内参矩阵和外参矩阵均已得到。

3 标定相机的畸变参数

张正友标定法仅仅考虑了畸变模型中影响较大的径向畸变。

径向畸变公式（2阶）如下：

$$\begin{array}{c}\hat{x}=x(1+k_1{r}^2+k_2{r}^4)\\ \hat{y}=y(1+k_1{r}^2+k_2{r}^4)\end{array}$$

其中，(x, y),($\hat{x}$,$\hat{y}$)分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标，r 为图像像素点到图像中心点的距离，即 r²=x²+y² 。

图像坐标和像素坐标的转化关系为：
$$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{dX}& -\frac{cot\theta }{dX}& u_0\\ 0& \frac{1}{dYsin\theta }& v_0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

其中, (u,v)为理想的无畸变的像素坐标。由于 θ 接近于 90∘ ，则上式近似为
$$\begin{array}{c}u=x/dX+u_0\\ v=y/dY+v_0\end{array}$$
同理可得畸变后的像素坐标 ($\hat{u}$,$\hat{v}$)的表达式为：
$$\begin{array}{c}\hat{u}=\hat{x}/dX+u_0\\ \hat{v}=\hat{v}/dY+v_0\end{array}$$
代入径向畸变公式（2阶）则有：
$$\begin{array}{c}\hat{u}-u_0=(u-u_0)(1+k_1{r}^2+k_2{r}^4)\\ \hat{v}-v_0=(v-v_0)(1+k_1{r}^2+k_2{r}^4)\end{array}$$
可化简得：
$$\begin{array}{c}\hat{u}=u+(u-u_0)(k_1{r}^2+k_2{r}^4)\\ \hat{v}=v+(v-v_0)(k_1{r}^2+k_2{r}^4)\end{array}$$
即为：
$$\begin{array}{c}\left[\begin{array}{cc}(u-u_0)r^2& (u-u_0)r^4\\ (v-v_0)r^2& (v-v_0)r^4\end{array}\right]\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=\left[\begin{array}{c}\hat{u}-u\\ \hat{v}-v\end{array}\right]\end{array}$$
上式中的$\hat{u}$，$\hat{v}$ 可以通过识别标定板的角点获得，每一个角点可以构造两个上述等式。有m幅图像，每幅图像上有n个标定板角点，则将得到的所有等式组合起来，可以得到个mn未知数为的k=[k₁,k₂]^T 约束方程，将约束方程系数矩阵记为D ，等式右端非齐次项记为d ，可将其记着矩阵形式：
$$\begin{array}{c}Dk=d\end{array}$$
则使用最小二乘法可求得：
$$\begin{array}{c}k=\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=(D^{T}D{)}^{-1}{D}^{T}d\end{array}$$
此时，相机的畸变矫正参数已经标定好。

需要指出，上述公式推导的时候以2阶径向畸变为例，但实际上更高阶的径向畸变同理，只是需要的约束方程个数更多而已。

4、L-M算法参数优化