相机标定基本原理

本文将简单介绍相机标定的理论基础，为了后续实践打好基础。

1. 相机内部参数标定

1.1 理想相机成像原理

在理想情况下，相机成像模型通常采用线性小孔成像模型表示。根据前一篇介绍的相机标定的四个坐标系及其关系，假设某个空间三维点 $P$ 的世界坐标为 $(X_w,Y_w,Z_w,1)^T$ ，其对应的投影点 $p$ 的像素坐标为 $(u,v,1)^T$ 。旋转矩阵 $R$ 表示旋转运动，平移矩阵 $t$ 表示平移运动。投影矩阵 $M$ 表示空间中的三维信息与图像的二维信息之间的投影变换。三维点 $P$ 的世界坐标与其对应投影点 $p$ 的像素坐标在理想相机成像模型下的关系为：

$s\left [ \begin{matrix} u\\ v\\ 1 \end{matrix} \right ]=\left [ \begin{matrix} \frac{1}{dX} & 0 & u_0\\ 0 & \frac{1}{dY} & v_0\\ 0 & 0 & 1 \end{matrix} \right ]\left [ \begin{matrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{matrix} \right ]\left [ \begin{matrix} R & t\\ 0 & 1 \end{matrix} \right ]\left [ \begin{matrix} X_w\\ Y_w\\ Z_w\\ 1 \end{matrix} \right ]=\left [ \begin{matrix} f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 1 \end{matrix} \right ]\left [ \begin{matrix} R & t\\ 0 & 1 \end{matrix} \right ]\left [ \begin{matrix} X_w\\ Y_w\\ Z_w\\ 1 \end{matrix} \right ]=KT\left [ \begin{matrix} X_w\\ Y_w\\ Z_w\\ 1 \end{matrix} \right ]=M\left [ \begin{matrix} X_w\\ Y_w\\ Z_w\\ 1 \end{matrix} \right ]$

其中， $f_x$ 和 $f_y$ 是相机归一化焦距， $K$ 是相机内部参数矩阵， $T$ 是相机外部参数矩阵。

1.2 相机非线性模型及畸变矫正

在实际相机成像过程中，由于相机镜头的加工误差或相机组装偏差的存在，实际相机成像模型与相机理想线性模型之间存在畸变，因此在相机理想成像模型的基础上引入畸变模型，便组成了相机成像的非线性模型。虽然相机非线性模型相对相机理想线性模型更加复杂，但是相机非线性模型更加接近相机真实成像模型。相机畸变简单来说就是实际三维空间中的一条直线投影到图像上无法继续保持为一条直线，如图1所示空间三维点在图像平面上实际投影点与理想投影点之间存在偏差。通常相机畸变分为径向畸变和切向畸变。

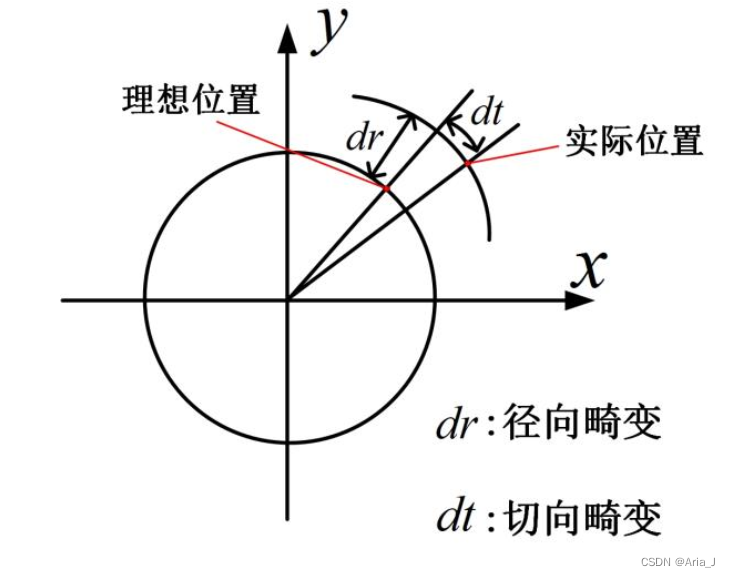
1. 径向畸变

如图2所示，径向畸变表现为实际的直线在图像边缘比靠近图像中心的地方更加弯曲。默认相机透镜的光学中心的径向畸变为0，越靠近图像边缘，径向畸变越严重。对于径向畸变可以通过下面的泰勒级数展开式进行矫正：

$x_{c,r}=x(1+k_1+r^2+k_2r^4+k_3r^6)$

$y_{c,r}=y(1+k_1r^2+k_2r^4+k_3r^6)$

其中， $(x,y)$ 是图像平面上某一点带有畸变的图像平面坐标（也就是原始图像平面坐标）， $(x_{c,r},y_{c,r})$ 是该点通过畸变矫正得到的去除径向畸变的坐标， $r$ 是该点距成像中心的距离。

2. 切向畸变

切向畸变是由于在相机组装过程中相机透镜与成像平面不能保证严格平行导致的。切向畸变可以通过如下方程式进行矫正：

$x_{c,t}=x+[2p_1xy+p_2(r^2+2x^2)]$

$y_{c,t}=y+[2p_2xy+p_1(r^2+2y^2)]$

其中， $(x_{c,t},y_{c,t})$ 是通过切向畸变矫正得到的去除切向畸变的坐标。

根据上面的介绍，对于某个空间三维点 $P$ 对应的投影点 $p$ 的图像平面坐标 $(x,y)$ ，进行径向畸变和切向畸变矫正后的坐标为 $(x_{corrected},y_{corrected})$ ，将畸变矫正后的点转换到像素坐标系，得到该点的图像平面上的像素坐标 $(u,v)$

$x_{corrected}=x(1+k_1r^2+k_2r^4+k_3r^6)+[2p_1xy+p_2(r^2+2x^2)]$

$y_{corrected}=y(1+k_1r^2+k_2r^4+k_3r^6)+[2p_2xy+p_1(r^2+2y^2)]$

$u=f_xx_{corrected}+u_0$

$v=f_yy_{corrected}+v_0$

其中，5个畸变系数可以组成畸变系数矩阵 $D=(k_1,k_2,p_1,p_2,k_3)$ 。

1.3 基于棋盘格标定板的相机标定方法

现有的相机标定方法主要利用投影几何关系将空间三维信息与相机采集的图像中的二维信息相关联，来计算相机内外参数。张正友标定法是经典的基于棋盘格标定板的相机标定方法。根据上一节的介绍可以把相机成像模型简化为：

$Z_c \left[ \begin {matrix} u\\ v\\ 1 \end {matrix} \right] = M\left [ \begin{matrix} X_w\\ Y_w\\ Z_w\\ 1 \end{matrix} \right ]$

假设世界坐标的原点建立在棋盘格标定板上，且棋盘格标定板所在的平面设置为世界坐标系的 $X_wO_wY_w$ 平面，则棋盘格标定板上某一点特征点的世界坐标可以表示为 $(X_w,Y_w,0,1)$ 。假设该点对应的投影点的像素坐标为 $(u,v,1)$ ，则两者之间的关系为

$Z_c\left [ \begin{matrix} u\\ v\\ 1 \end{matrix} \right ]=H\left [ \begin{matrix} X_w\\ Y_w\\ 1 \end{matrix} \right ]$

假设 $H=\left [ \begin{matrix} \vec{h_1} & \vec{h_2} & \vec{h_3} \end{matrix} \right ]$ ，将上面两式组合，可得：

$\left [ \begin{matrix} \vec{h_1} & \vec{h_2} & \vec{h_3} \end{matrix} \right ]=\lambda K\left [ \begin{matrix} \vec{r_1} & \vec{r_2} & t \end{matrix} \right ]$

其中， $\lambda$ 是非零常数， $\vec{r_1},\vec{r_2},\vec{r_3}$ 是旋转矩阵的列向量。

由于旋转矩阵 $R$ 有两大属性：

（1）旋转矩阵 $R$ 的列向量相互正交，即 $\vec{r_1}\vec{r_2}=0$

（2）旋转矩阵 $R$ 的列向量的模相等而且模为1，即 $\left | \vec{r_1} \right |=\left | \vec{r_2} \right |=1$ ，因此存在如下关系：

$\vec{h_1}^{T}K^{-T}K^{-1}\vec{h_2}=0$

$\vec{h_1}^{T}K^{-T}K^{-1}\vec{h_1}=\vec{h_2}^{T}K^{-T}K^{-1}\vec{h_2}$

假设 $B=K^{-T}K^{-1}=\left [ \begin{matrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{matrix} \right ]$

此时考虑扭曲因子 $\gamma$ ，因此相机内参可以表示为：

$K=\left [ \begin{matrix} f_u & \gamma & u_0 \\ 0 & f_v & v_0\\ 0 & 0 & 1 \end{matrix} \right ]$

将 $K$ 带入 $B$ 可得：

$B=K^{-T}K^{-1}=\left [ \begin{matrix} \frac{1}{f_{u}^{2}} & -\frac{\gamma }{f_{u}^{2}f_v} & \frac{\gamma v_0-u_0f_v}{f_{u}^{2}f_v}\\ -\frac{\gamma }{f_{u}^{2}f_v} & \frac{\gamma }{f_{u}^{2}f_v}+\frac{1}{f_{v}^{2}} & -\frac{\gamma (\gamma v_0-u_0f_v)}{f_{u}^{2}f_{v}^{2}}-\frac{v_0}{f_{v}^{2}}\\ \frac{\gamma v_0-u_0f_v}{f_{u}^{2}f_v} & -\frac{\gamma (\gamma v_0-u_0f_v)}{f_{u}^{2}f_{v}^{2}}-\frac{v_0}{f_{v}^{2}} & \frac{(\gamma v_0-u_0f_v)^2}{f_{u}^{2}f_{v}^{2}}+\frac{v_{0}^{2}}{f_{v}^{2}}+1 \end{matrix} \right ]$

由上式可知， $B$ 为对称矩阵，因此 $B$ 只有6个参数，则将 $B$ 改写成6维向量：

$\vec{b}=\left [ \begin{matrix} b_{11} & b_{12} & b_{22} & b_{13} & b_{23} &b_{33} \end{matrix} \right ]^T$

假设 $H$ 的第 $i$ 列向量是 $\vec{h_i}=\left [ \begin{matrix} h_{i1} & h_{i2} & h_{i3} \end{matrix} \right ]^T$ ，故

$\vec{h_i}^TB\vec{h_j}=c_{ij}^{T}\vec{b}$

其中， $c_{ij}=\left [ \begin{matrix} h_{i1}h_{j1}, & h_{i1}h_{j2}+h_{i2}h_{j1}, & h_{i2}h_{j2}, & h_{i3}h_{j1}+h_{i1}h_{j3}, & h_{i3}h_{j2}+h_{i2}h_{j3}, & h_{i3}h_{j3} \end{matrix} \right ]^T$

结合旋转矩阵 $R$ 的两大属性，可以得到：

$\left [ \begin{matrix} c_{12}^{T} \\ (c_{12}-c_{22})^T \end{matrix} \right ]\vec{b}=C\vec{b}=0$

若存在L张标定图像，则 $C$ 是 $2L\times 6$ 的矩阵，当 $L\geq 3$ 时，方程有关于向量 $\vec{b}$ 的唯一解。当向量 $\vec{b}$ 确定时，内参矩阵 $K$ 也可确定。同时根据旋转矩阵 $R$ 的属性，每张标定图像的外参由下式计算得到：

$\left\{\begin{matrix} \vec{r_1}=\lambda K^{-1}\vec{h_1}\\ \vec{r_2}=\lambda K^{-1}\vec{h_2}\\ \vec{r_3}=\vec{r_1}\times \vec{r_2}\\ t=\lambda K^{-1}\vec{h_3} \end{matrix}\right.$

其中，

$\lambda =\frac{1}{\left \| K^{-1}\vec{h_1} \right \|}=\frac{1}{\left \| K^{-1}\vec{h_2} \right \|}$

在得到相机内外参数的初始估计值后，利用最小化重投影误差的方式来对内外参数的估计值进行优化，即：

$min\sum_{i=1}^{n}\sum_{j=1}^{m}\left \| p_{ij}-p(K,D,R_{i},t_{i},P_{j}) \right \|^2$

其中， $p(K,D,R_i,t_i,P_j)$ 是 $P_{j}$ 利用相机内外参数计算出的投影点的预测值。 $p_{ij}$ 是相机在 $\left [ R_i, t_i \right ]$ 位姿时图像上 $P_j$ 的投影点的检测值。

2. 特征提取与匹配

多相机系统外部参数时不同相机之间在同一世界坐标系下的三维空间位姿关系，包括相机坐标系与参考坐标系之间的旋转矩阵和平移矩阵，因此在对相机进行外部参数标定时，首先需要确定同一个世界坐标系，即统一参考标准。假设已知相机所在场景的三维结构，并将此三位结构作为相机外部参数标定的参考标准，来说明相机外部参数标定的原理。相机外部参数标定的方法有直接法和特征点法。直接法基于灰度不变的假设，首先根据第一张图像的位姿估计结果来寻找第二张图像中的特征点的投影位置，其次通过最小化两个像素的光度误差优化特征点的投影位置。直接法计算相机位置的前提是假设一个空间三维点在各个视角下成像的灰度保持不变，但是实际应用中灰度值易受光照或相机位置的影响。当光照发生变化或相机变换位姿，图像的灰度值发生变化时，直接法计算相机位姿可能发生错误。特征点法手光照影响不大，相对直接法有更好的鲁棒性。因此，我们直接介绍特征点法进行相机定位。

特征点是图像中比较有代表性的点，在相机发生少量运动时图像中的特征点保持稳定，仍可以在不同图像上判断同一个特征点，进而利用同一个特征点计算不同图像之间的运动关系。常见的图像特征点检测算法有：SIFT、SURF、ORB等。SIFT算法充分考虑图像采集过程中的光照、尺度、旋转等变化，具有高精度的特点，但是其计算量极大，导致计算速度过慢。SURF算法优化了SIFT算法，提高了算法计算速度。另外ORB算法图像特征提取酸度更快并且在一定程度上不受噪声点和图像变换的影响。本文采用ORB算法进行特征点检测的过程分为两个步骤：

1. FAST角点提取。首先设置最终提取角点的数量为N，对FAST角点分别计算Harris响应值，选取N个具有最大响应值的角点，组成角点集合；然后通过构建图像金字塔实现尺度不变性；最后利用灰度质心法确定图像主方向。

2. BRIEF描述子。ORB算法利用BRIEF描述子对FAST角点进行描述，由许多0和1组成，用来表示关键点周围的像素亮度的明暗关系。

ORB算法采用BRIEF描述子中的0和1描述了关键点附近两个像素（比如p和q）的明暗关系：如果 $p>q$ ，则取1，否则取0。若随机选取关键点周围256个p和q，则可以得到256维的二进制向量，即每个特征点有一个256维的二进制描述子。不妨假设在某张图像 $I_t$ 中提取M个特征点 $x_{t}^{m} (m=1,2,...,M)$ ，在图像 $I_{t+1}$ 中提取到N个特征点 $x_{t+1}^{n} (n=1,2,...,N)$ 。首先计算图像 $I_t$ 中的每个特征点 $x_{t}^{m}$ 和图像 $I_{t+1}$ 中的所有特征点 $x_{t+1}^{n}$ 描述子之间的汉明距离，然后选取汉明距离最小的 $x_{t+1}^{n}$ 为 $x_{t}^{m}$ 的匹配点，最后依次计算 $I_t$ 中所有特征点相应的匹配点，完成图像 $I_t$ 和 $I_{t+1}$ 的匹配。