【算法题】动态规划中级阶段之不同的二叉搜索树、交错字符串

前言

动态规划（Dynamic Programming，简称 DP）是一种解决多阶段决策过程最优化问题的方法。它是一种将复杂问题分解成重叠子问题的策略，通过维护每个子问题的最优解来推导出问题的最优解。

动态规划的主要思想是利用已求解的子问题的最优解来推导出更大问题的最优解，从而避免了重复计算。因此，动态规划通常采用自底向上的方式进行求解，先求解出小规模的问题，然后逐步推导出更大规模的问题，直到求解出整个问题的最优解。

动态规划通常包括以下几个基本步骤：

1. 定义状态：将问题划分为若干个子问题，并定义状态表示子问题的解；
2. 定义状态转移方程：根据子问题之间的关系，设计状态转移方程，即如何从已知状态推导出未知状态的计算过程；
3. 确定初始状态：定义最小的子问题的解；
4. 自底向上求解：按照状态转移方程，计算出所有状态的最优解；
5. 根据最优解构造问题的解。

动态规划可以解决许多实际问题，例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。同时，动态规划也是许多其他算法的核心思想，例如分治算法、贪心算法等。

动态规划是一种解决多阶段决策过程最优化问题的方法，它将复杂问题分解成重叠子问题，通过维护每个子问题的最优解来推导出问题的最优解。动态规划包括定义状态、设计状态转移方程、确定初始状态、自底向上求解和构造问题解等步骤。动态规划可以解决许多实际问题，也是其他算法的核心思想之一。

一、不同的二叉搜索树

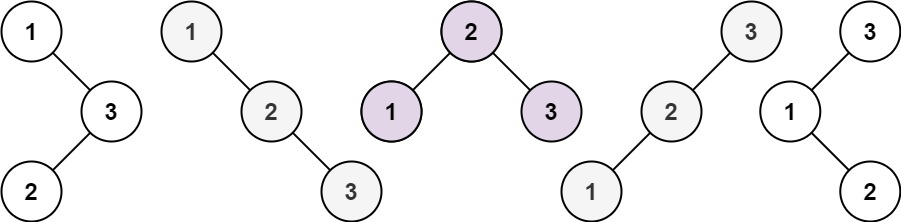
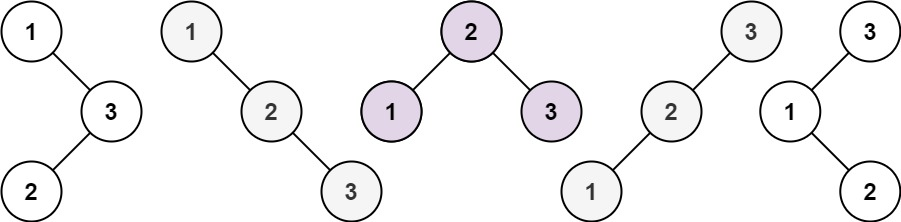
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

来源：力扣（LeetCode）。

1.1、思路

方法一：动态规划 思路 给定一个有序序列 $1\cdots n$，为了构建出一棵二叉搜索树，我们可以遍历每个数字 $i$，将该数字作为树根，将 $1\cdots (i-1)$ 序列作为左子树，将 $(i+1)\cdots n$ 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的。

由此可见，原问题可以分解成规模较小的两个子问题，且子问题的解可以复用。因此，我们可以想到使用动态规划来求解本题。

假设 n 个节点存在二叉排序树的个数是 G (n)，令 f(i) 为以 i 为根的二叉搜索树的个数，则G(n)=f(1)+f(2)+f(3)+f(4)+…+f(n)。

当 i 为根节点时，其左子树节点个数为 i-1 个，右子树节点为 n-i，则f(i)=G(i−1)∗G(n−i)。

综合两个公式可以得到 卡特兰数 公式：G(n)=G(0)∗G(n−1)+G(1)∗(n−2)+…+G(n−1)∗G(0)。

1.2、代码实现

class Solution {
    
    
public:
    int numTrees(int n) {
    
    
        vector<int> G(n + 1, 0);
        G[0] = 1;
        G[1] = 1;

        for (int i = 2; i <= n; ++i) {
    
    
            for (int j = 1; j <= i; ++j) {
    
    
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
};

时间复杂度：$O(n^2)$。
空间复杂度：O(n)。

二、不同的二叉搜索树 II

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

输入：n = 1
输出：[[1]]

来源：力扣（LeetCode）。

2.1、思路

1. dp数组的含义：dp[i]表示序列[1,2,3,…,i]能够形成的所有不同BST。
2. basecase：i=0 时为空树，i=1 时为只有一个根节点1的树。
3. 状态转移：为了得到dp[i]，在区间[1,i]枚举所有的j，以j作为BST的根节点，可以得到左边序列的所有二叉搜索树dp[j−1]、j右边序列的所有平衡二叉树dp[i−j]。不过这里的dp[i−j]是序列[1,…i−j]构成的BST，只要对它们做深拷贝并将每个节点值加j，就可以得到序列[j+1,…i]构成的BST，这正是我们需要的。现在已知j左边序列的BST和右边序列的BST，只需要用两个for循环，左边序列BST作为j的左子树，右边序列BST作为j的右子树，就可以得到所有节点值为1到i且以j作为根节点的BST，然后遍历j+1重复相同流程即可。

2.2、代码实现

class Solution {
    
    
public:
    // 对tmp做深拷贝并将每个节点值加j
    TreeNode* copy_tree(TreeNode* tmp, int j){
    
    
        if(tmp == nullptr) return nullptr;   
        TreeNode* left = copy_tree(tmp->left, j);
        TreeNode* right = copy_tree(tmp->right, j);
        TreeNode* node = new TreeNode(tmp->val + j, left, right);
        return node;
    }
    vector<TreeNode*> generateTrees(int n) {
    
    
        // dp[i]表示序列[1,2,...,i]能够形成的所有不同BST
        vector<vector<TreeNode*>> dp(n+1);
        dp[0] = {
    
    nullptr};
        dp[1] = {
    
    new TreeNode(1)};
        for(int i = 2;i <= n;i++){
    
    
            // 在[1,i]范围枚举所有j，以j为根节点，左边序列BST成为j的左子树，右边序列BST成为j的右子树
            for(int j = 1;j <= i;j++){
    
    
                // 一共有dp[j-1]*dp[i-j](左序列*右序列)种组合，全部遍历
                for(auto& tmp: dp[i-j]){
    
    
                    TreeNode* rson = copy_tree(tmp, j); // tmp不能直接当右孩子，要整体加j并做深拷贝
                    for(auto& lson: dp[j-1]){
    
    
                        dp[i].push_back(new TreeNode(j, lson, rson));
                    }
                }
            }
        }
        return dp[n];
    }
};

三、交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

• s = s1 + s2 + … + sn
• t = t1 + t2 + … + tm
• |n - m| <= 1
• 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

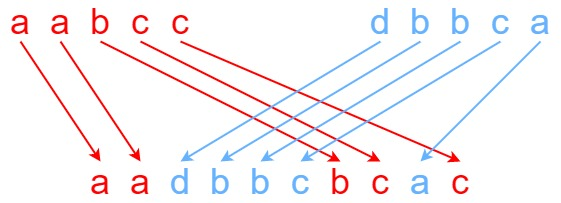
输入：s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出：true

示例 2：

输入：s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出：false

示例 3：

输入：s1 = “”, s2 = “”, s3 = “”
输出：true

来源：力扣（LeetCode）。

3.1、思路

dp[i][j]表示s1长度i,s2长度j能不能组成长度为i+j的s3。

3.2、代码实现

class Solution {
    
    
public:
    bool isInterleave(string s1, string s2, string s3) {
    
    
        int len1=s1.size();
        int len2=s2.size();
        int len3=s3.size();
        if(len1+len2!=len3){
    
    
            return false;
        }
        if(len1==0&&len2==0){
    
    
            return true;
        }
        //dp[i][j]表示s1长度i,s2长度j能不能组成长度为i+j的s3
        vector<vector<int>> dp(len1+1,vector<int>(len2+1));
        dp[0][0]=1;
        for(int i=1;i<=len1;i++){
    
    
            if(s1[i-1]==s3[i-1]){
    
    
                dp[i][0]=dp[i-1][0];
            }else{
    
    
                dp[i][0]=0;
            }
        }
        for(int i=1;i<=len2;i++){
    
    
            if(s2[i-1]==s3[i-1]){
    
    
                dp[0][i]=dp[0][i-1];
            }else{
    
    
                dp[0][i]=0;
            }
        }
        for(int i=1;i<=len1;i++){
    
    
            for(int j=1;j<=len2;j++){
    
    
                int flag1=dp[i][j-1]*(s2[j-1]==s3[i+j-1]? 1 :0);
                int flag2=dp[i-1][j]*(s1[i-1]==s3[i+j-1]? 1 :0);
                int x=flag1+flag2;
                if(x>0){
    
    
                    dp[i][j]=1;
                }else{
    
    
                    dp[i][j]=0;
                }
            }
        }
        return dp[len1][len2];
    }
};

总结

动态规划（Dynamic Programming）是一种解决多阶段决策最优化问题的方法，它将复杂问题分解成重叠子问题并通过维护每个子问题的最优解来推导出问题的最优解。动态规划可以解决许多实际问题，例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。

动态规划的基本思想是利用已求解的子问题的最优解来推导出更大问题的最优解，从而避免了重复计算。它通常采用自底向上的方式进行求解，先求解出小规模的问题，然后逐步推导出更大规模的问题，直到求解出整个问题的最优解。

动态规划通常包括以下几个基本步骤：

1. 定义状态：将问题划分为若干个子问题，并定义状态表示子问题的解；
2. 定义状态转移方程：根据子问题之间的关系，设计状态转移方程，即如何从已知状态推导出未知状态的计算过程；
3. 确定初始状态：定义最小的子问题的解；
4. 自底向上求解：按照状态转移方程，计算出所有状态的最优解；
5. 根据最优解构造问题的解。

动态规划的时间复杂度通常为$O(n^2)$或$O(n^3)$，空间复杂度为O(n)，其中n表示问题规模。在实际应用中，为了减少空间复杂度，通常可以使用滚动数组等技巧来优化动态规划算法。