本文将从SGD开始介绍Adam优化器的原理以及其变种的提出背景。
1、SGD的原理
SGD(随机梯度下降法)是基于最速梯度下降法的原理,假设我们存在损失函数,其中
是要学习参数,定义如下的优化路径
,使得损失函数
值最小。这是一个不断更新迭代参数
的过程,其中
表示其中某一更新步,
表示更新步长(即学习率),
表示更新方向。
假设存在最优参数,当前参数为最优参数附近的
,我们选择合适的参数更新步长,使得
逼迫最优参数。我们对目标损失函数
进行泰勒展开:
因为是最优参数,所以:
最速下降法是指在规范化的基础上,找到一个合适的值使得方向导数
最小,或者说让
近可能逼近最优值
,假设是L2范式
时,当
时,方向导数最小。因此最速下降法的更新路径可以表示为:
其中表示更新步长,因为上述泰勒展开式包含要求是在参数附近进行更新,因此需要控制更新的步长,其在SGD中称之为学习率。
2、SGD with Momentum 动量SGD的原理
因为在SGD中方向梯度可能会因为某些点偏差会造成参数学习的振荡,因此通过动量来添加平滑参数:
3、Adam的原理
动量SGD解决了由于梯度在某些点偏差会带来学习的振荡,但同时学习率设置也会影响学习,当梯度较小时,学习率设置过小,会减缓训练速度,而当梯度较大,学习率如果设置过大,会造成训练的振荡,因为Adam在动量SGD基础上增加了自适应调整学习率(即更新步长)。
Adam在动量SGD的基础上增加了二阶动量,通过其来自适应控制步长,当梯度较小时,整体的学习率
就会增加,反之会缩小,因此在一般情况下,Adam相较于SGD,其收敛速度要更快。
同时为了避免某些点梯度偏差带来学习率的振荡,因此通过引入动量特性(由于梯度二次情况下,一般
)。
4、AdamW的原理
但是Adam存在另外的问题,当loss函数中存在L2正则项时,采用Adam优化并不会有效,主要原因是Adam的学习率是变化的,而且当梯度变大时,其学习率会变小,因此会使梯度较大的权重参数同梯度较小的权重参数相差更大,这同L2正则是相违背的。我们通过公式来说明这个过程:
假设目标损失函数添加了L2正则项后,如下表示为:
如果通过动量SGD作为优化器,此时参数的更新可以写为如下式,同时可以看出L2正则项同weight decay也是等价的。
但是当Adam应用时,weight decay系数当梯度较大时其值较小,使得Adam对于L2正则项的优化并不好。因此AdamW主要是在Adam中增加了weight decay项,来帮助优化L2正则项:
上式中的为weight decay的系数,其中b表示batch size,B表示epoch中训练的batch数,T表示总共的epoch数,可以看出weight decay系数同整个训练轮数有关系。
5、AdamWR的原理
AdamWR主要是添加了热重启warm restart功能,其解决的问题是避免模型训练陷入局部最优,因为学习率和梯度会一直收敛,当达成局部最优点时,很难或者要很长时间才能跳出来,因此AdamWR主要是通过周期性增大学习率,从而提升模型的探索空间。
这个周期性调整学习率的函数称为cosine annealing,可以表示为:
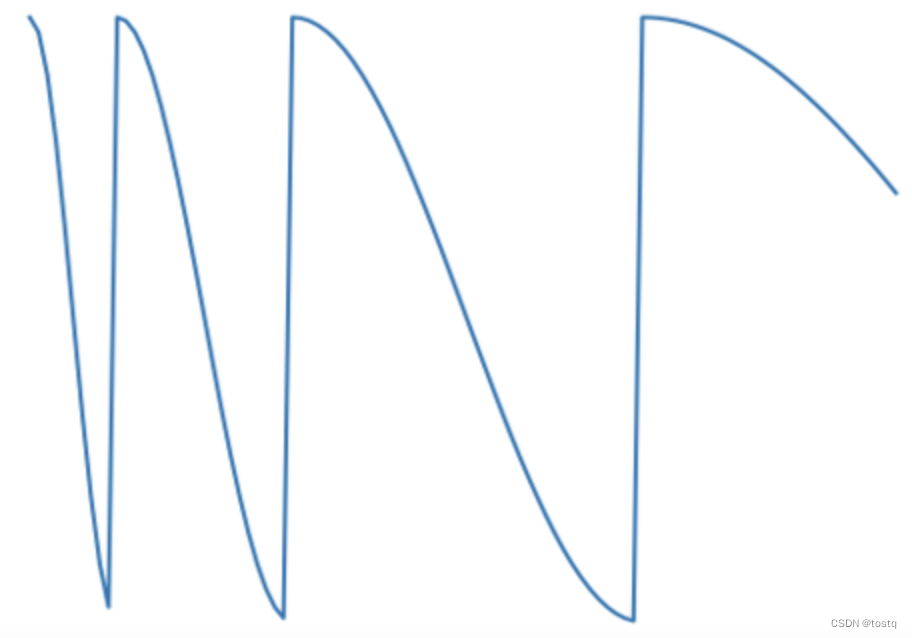
AdamWR将整个训练过程分为多个热重启过程,上式中的i表示为第i个热重启过程,表示在该阶段中最小的学习率,
表示当前热重启轮中总共需要训练epoch数,
表示当前已经训练的epoch数。
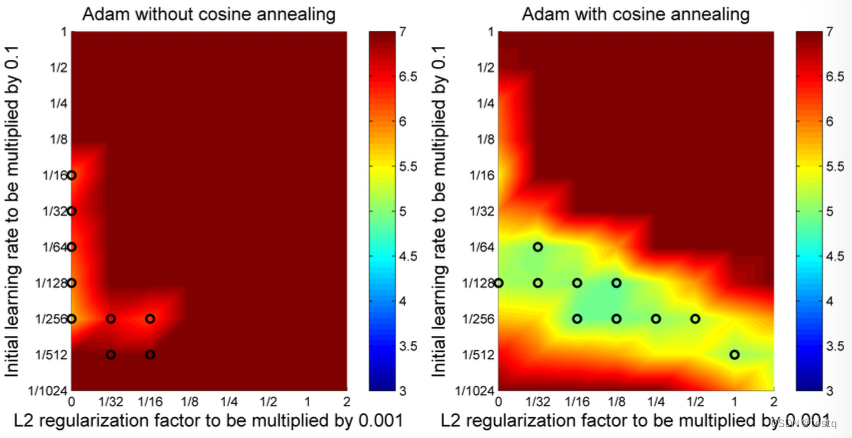
通过AdamWR的模型的探索空间更大,下图评估了在不同初始学习率和L2正则项权重值的情况下,AdamWR所能找到的优点空间更大。