龙贝格积分——matlab实现

日期：2019-11-12
作者：老李

实验报告

龙贝格积分关于MATLAB实现

目标：

1.应用MATLAB实现龙贝格积分
2.打印龙贝格积分表

过程：

1.重要理论：

递归梯形公式：

由 $T(0) = (h/2)(f(a)+f(b))$开始，梯形公式序列 ${T(J)}$可由以下递归公式生成： $T(J) =\frac{T(J-1)}{2}+h\sum_{k=1}^{M}f(x_{2k-1})$
其中 $h=(b-a)/2^{J},{x_{k} = a+kh}$

龙贝格积分：

设用步长 $h$和 $2h$得到一个逼近公示的两个结果，则两个结果的代数运算将得到改进的答案。每次改进将误差项的阶由 $O(h^{2N})$提高到 $O(h^{2N+2})$。该过程称为龙贝格积分。

龙贝格积分的一个缺点是，为了将误差由 $O(h^{2N})$降低到 $O(h^{2N+2})$，函数求值次数增加了一倍

应用理查森外推思想的龙贝格积分

给定 $Q$的两个逼近 $R(2h, K-1)$和 $R(h, K-1)$,满足
$Q = R(h, K-1) + c_{1}h^{2K}+c_{2}h^{2K+2}+...$
和 $Q = R(2h, K-1) + c_{1}4^{K}h^{2K}+c_{2}4^{K+1}h^{2K+2}+...$其改进的逼近为
$Q = \frac{4^{K}R(h, K-1)-R(2h, K-1)}{4^{K}-1}+O(h^{2K+2})$
我们从而可以得到龙贝格积分表：

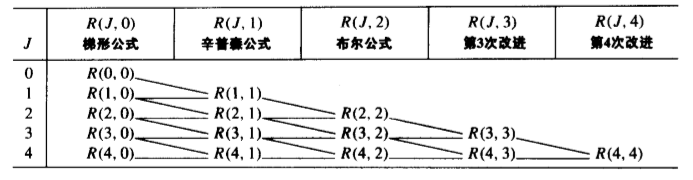
2.MATLAB实现

生成 $J\geqslant K$的逼近表 $R(J, K)$，并以 $R(J+1,J+1)$为最终解来逼近积分 $\int_{a}^{b}f(x)dx\approx R(J,J)$
逼近 $R(J,K)$存在于一个特别的下三角矩阵中，第0列元素 $R(J,0)$用基于 $2^{J}$个 $[a,b]$子区间的连续提醒方法计算，然后利用龙贝格公式计算 $R(J,K)$。

当 $1\leqslant K\leqslant J$时，第 $J$行的元素为
$R(J,K) = R(J,K-1) + \frac{R(j, k-1)-R(J-1, K-1)}{4^{K}-1}$
当 $|R(J,J)-R(J+1,J+1)|<tol$时，程序在第（J+1）行结束

代码如下：

function [ R, q, err0, err1, h ] = rombergIntegration( f, a, b, n, tol0, tol1)
%rombergIntegration: to count the integration of f in [a,b] 
%by using romberg method
% Input: -          f is the intergrand input by using function handle
%        -          a and b are upper and lower limits of integration
%        -          n is the maximum number of rows in the table
%        -          tol0 is the tolerance for 
%real integration and romberg integration
%        -          tol1 is the tolerance for each iteration
%Output: -          R is the Romberg table
%        -          q is the quadrature value
%        -          err0 is the error between real integration and romberg
%        integration
%        -          err1 is the error between final iteration
%        -          h is the smallest step size used
M = 1;%记录每次的步数
h = b-a;%最大步长
y = integral(f,a,b);%计算实际积分值
err0 = 1;%给真值和计算值的差赋予初值
err1 = 1;%给前后迭代差值赋予初值
J = 0;%龙贝格积分表的行
R = zeros(n,n);%分配矩阵大小
R(1,1) = h*(feval(f,a)+feval(f,b))/2;%第一个值
while (err>tol)&&(J<n)%迭代条件
    J = J+1;
    h = h/2;
    s = 0;
    %构造一列中，上下行元素之间的关系
    for p = 1:M
        x = a+h*(2*p-1);
        s = s+feval(f,x);
    end
    R(J+1, 1) = R(J, 1)/2+h*s;
    %更新步数
    M = 2*M;
    %构造一行中，左右列元素之间的关系
    for K=1:J
        R(J+1, K+1) = R(J+1, K)+(R(J+1,K)-R(J,K))/(4^K-1);
    end
    %表示绝对误差
    err1 = abs(R(J,J)-R(J+1,K+1));
    err0 = abs(R(J+1,K+1)-y);
end
%表示最终所得的积分值
q = R(J+1,J+1);
end

3.结果

我们打算计算这样一个积分：
$\int_{0}^{1}e^{x}dx$

输入参数：

f = @(x)exp(x)
a = 0
b = 1
n = 8
tol0 = eps
tol1 = eps

结果如下：