定点数和浮点数以及float32的最值求解

1 定点数

定点数中小数点的位置是不变的。

1.1 定点小数

表示$(0,1)$内的小数的被称为定点小数，小数点的位置是隐含在数值位最高位的左边。定点小数只能表示纯小数，也就是$0.5$,$0.78$这样的小数，不能表示$1.5$.

1.2 定点整数

定点整数只能用来表示纯整数。其小数点隐含在数值位最低位的右边。

2 浮点数

对于类似$28.625$这样的数值，该如何在机器中表示呢？
以如下形式为例：

那么图中的这些名词都对应的是什么？

2.1 规格化

首先我们先将$28.625$转换为二进制。
对于二进制转换的一个技巧就是列表法。

16	8	4	2	1	0.5	0.25	0.125
1	1	1	0	0	1	0	1

所以，$(28.625{)}_{10}=(11100.101{)}_2$.

说起规格化可能大家会陌生，但是说到十进制中的科学计数法，大家都会熟悉。
而二进制的规格化也类似于科学计数法，不过基底换成了2。

$$N=M\times 2^E$$

因此$(11100.101{)}_2=0.11100101\times 2^{101}$。

然后我们再回顾前面的图，其中

• 数符：就是整个数字的正负号，1表示负号，0表示正号。该例中为0。
• 阶符：阶的符号，上边的例子中$2^{101}$里的101就是阶，是正数，所以阶符为0；
• 阶码：阶的数值，也就是101。
• 尾数：规格化后0.后的数， 本例是11100101

假设有这样的16位机器，阶符占1位，数符占1位，阶码占5位，尾数占9位（阶码不够位数的使用前置0凑齐，尾数不够位数的使用后置0凑齐）。因此$(28.625{)}_{10}$写成如下形式：

数符	阶符	阶码	尾数
0	0	00101	111001010

即0000101111001010。

3 IEEE 754标准下的浮点数表示

相信经过上述流程，大家已经对浮点数怎么转换有了一定的认知。

但是不同的规则下，转换出来的浮点数是不同的。

为了统一，因此目前都采用了IEEE 754制定的标准，如下图以float32为例。

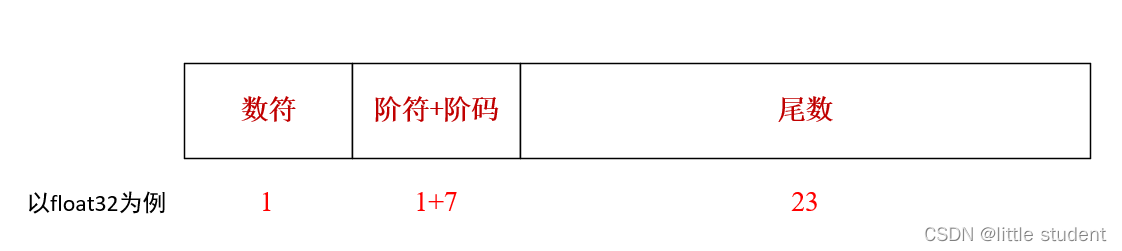
3.1 IEEE 754 规格化

与2.1小节不同的是，IEEE754采用将M调整到1.x的状态，同样以28.625为例。
$$(28.625{)}_{10}=(11100.101{)}_2=1.1100101\times 2^{100}$$

同时隐藏$1.1100101$中的$1.$
剩下的填入尾数并用0填满，因此尾数=11001010000000000000000

3.2 阶码

IEEE 754中并不是采用阶的原码填入第二栏。

而是用阶的十进制数+$2^k-1$,$k$指的阶占的位数，float32这里则是$2^8-1=127$，127转换成二进制则为01111111，这里+的这个数被叫做偏移量。

因此阶100，加上阶符0以及凑成8位得到原码为00000100。

• 原码：00000100
• 阶码：原码+01111111 = 10000010

3.3 转换

数符	阶符 +阶码	尾数
0	10000010	11001010000000000000000

4 float32最值

根据IEEE 754 标准，我们计算一下float32位的最大值和最小值。
虽然有很多文章已经探讨了float32取值范围的计算方法，但是要么是直接给出答案，要么就是解答错误。因此才有了以下的叙述。

4.1 特殊的浮点数

在开始探讨float32的最值之前，先声明几个特殊的浮点数形式。

4.1.1 0值

在介绍IEEE标准的浮点数时，M=1.x，如果按照这个标准，是无论尾数x是什么都没法表示0值的。因此对于0值，需要特殊声明：

• +0 = 0 00000000 00000000000000000000000
• -0 = 1 00000000 00000000000000000000000

如上所示，以阶全为0和尾数全为0表示0值。

4.1.2 无穷（Infinity）

以尾数全为0，阶全为1，表示无穷。

• +INFINITY = 0 11111111 00000000000000000000000
• -INFINITY = 1 11111111 00000000000000000000000

4.1.3 NaN值

以阶全为1，尾数不全为0，表示NaN值。
以下范围内的全为NaN值：

0 11111111 00000000000000000000001 ~ 0 11111111 11111111111111111111111

1 11111111 00000000000000000000001 ~ 1 11111111 11111111111111111111111

4.1.3 subnormal数

以如下数值为例：
$$0.00110001101001\ast 2^{-126}$$

如果以IEEE 754标准，则需将其转换成如下形式：
$$1.10001101001\ast 2^{-129}$$

而-129已经超过了8位数能够表示的范围。所以标准的IEEE 754是没法表示这样的数值的。

为了能够表示这样极小的数值，需要特殊规定如下subnormal数值（非正规化数值）。

非正规化数值的阶全为0，尾数不全为0.，规定其表示出来的数值是
$$0.x\ast 2^{-126}$$
$x$指的是尾数中的数值。

4.1.4 总结

这里的阶指的是阶符+阶码。

0	Infinity	NaN	Subnormal
尾数全为0，阶也全为0	尾数全为0，阶全为1	尾数不全为0，阶全为1	尾数全为0，阶不全为0

4.1 float32最大正数值

最大值其实不难想，使尾数和阶码都用1填满即可。

那就是如下图所示，0表示阶符，因为前面有个符号位，指数最大只能到127，

同时我们来看一个有意思的事情，我们以12为例，规格化后是
$(12{)}_{10}=(1.100\times 2^{11}{)}_2$

同时：

$(1.1{)}_2=(1.5{)}_{10}$

$(11{)}_2=(3{)}_{10}$

而$(1.5\times 2^3{)}_{10}=12$

因此可以发现，规格化后，我们同时将M和指数由2进制转换为10进制后，计算乘式得到的数值与原10进制的数值相等。

利用这个性质我们来研究上面图中的float32的最大值在10进制到底是多少。

而指数01111111转换为10进制就是127,
那么在float32最大值在10进制下的数值
$$max=(2-2^{-23})\times 2^{127}$$

使用计算器可以得到，$max=3.4028234663852\times 10^{38}$

由java文档对Float.MAX_VALUE的定义也可以看出，我们的计算结果是正确的。

4.2 float32最小正数值

4.2.1 float32最小normal正数值

求float32位的最小normal正数值是同样的道理，举一个例子：

• $0.1\times 2^{-1}=0.01$
• $0.1\times 2^2=1.0$
• $0.01\times 2^{-1}=0.001$

为了使得这个最小正数值尽可能的小，我们需要$M\times 2^E$中的$M$是一个正数且尽可能小的，$E$必须是负数且$E$的绝对值需要是一个尽可能大的数。

在normal这个范围内，是M=1.x，尾数x只能全为0，M才是最小。

而阶中本来-127的原码11111111+偏移量127=00000000，00000000用来表示subnormal number了,所以阶最小只能到-126.

所以float32在normal number范围时最小正数值：$\mathrm{1.00000...000}\times 2^{-126}=2^{-126}=1.175494350822\times 10^{-38}$
该结果与JAVA文档中的Float.MIN_NORMAL的介绍一致。

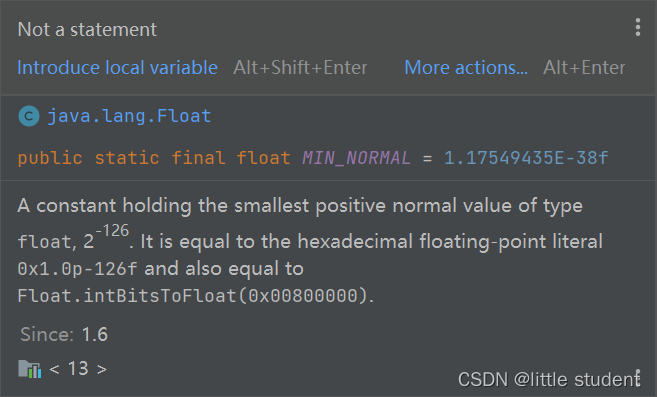
4.2.1 float32最小subnormal正数值

当阶全为0，尾数不全为0的时候是subnormal，如下情况是最小：

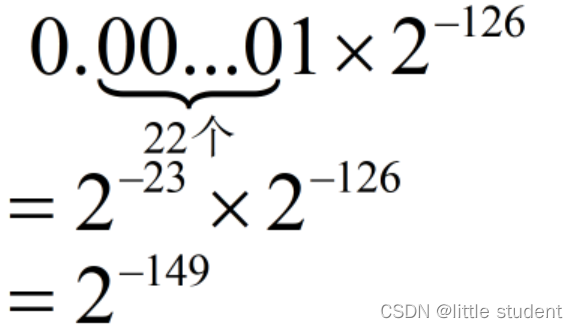
而$2^{-149}=1.401298464324^{-45}$,同样该结果与java文档中Float.MIN_VALUE保持一致。

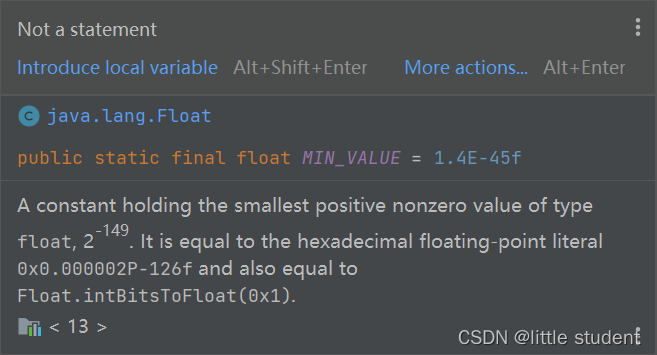
4.3 float32最小负数值

4.3 float32最大负数值

未完待续。可以自己尝试参考以上推理，推出最小负数值和最大负数值。