计算机中的浮点数
计算机中的float类型,有一篇文章写的很好,这里把它的一部分放过来:https://www.duote.com/tech/cyuyan/14691.html
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
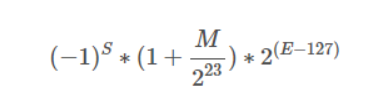
这里的s来自单词sign,是正负符号的意思,m来自于单词mantissa,意思是尾数,E来自于单词Exponent,意思是指数
也就是说,对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。如下图所示
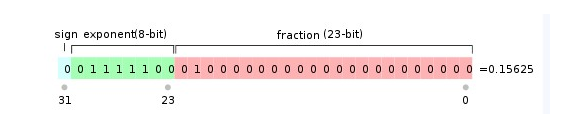
十进制里,我们是这么表示一个数的 X = (-1)^s * A * 10 ^ e,其中A在1~9之间,e是指数位,s是符号位,二进制的表示法也是类似的
在二进制计数法里:
- 符号位s是为了表示正负数,当s为1时表示负数,s为0时表示正数
- M是二进制表示的尾数,M的大小在0~8 388 607之间,(2^23 = 8388608),
1+M/2^23就表示了2进制里科学计数法的有效数字位,范围在1.0~1.99999988之间,也就是说,浮点数能表示的最接近2的数是1.99999988 - E是二进制表示的位数,32位的float分配了8位的内存,所以E在0~255之间,不过由于指数位既要考虑到整数,还要考虑到小于1的小数,所以这里的E要减去移位符127,否则对于
2^E而言,这个数永远是大于1的
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。如下图所示
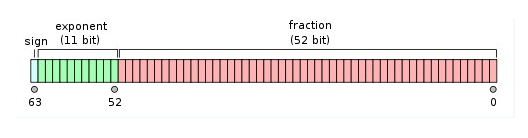
下面举一个例子,将十进制的3.14159转换为浮点数存储起来。
首先需要将3.14159转换为2进制表示,这个就不多说了,小数部分,可以通过计算器得到,如下图所示:
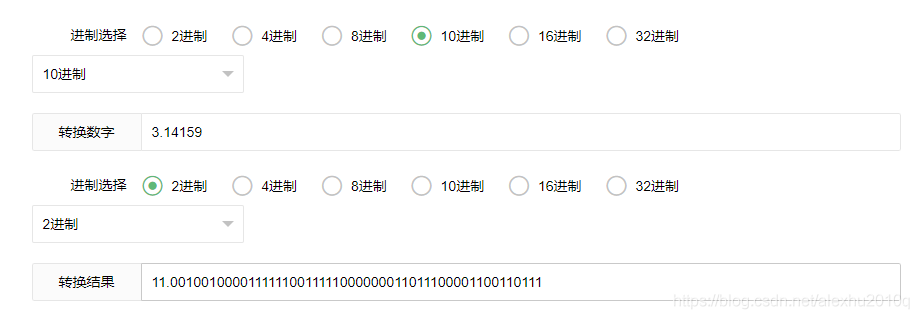
可以看到结果很长很长,说明用2进制表示,这可能是一个无理数,只取前面的23位,11.0010 0100 0011 1111 0011 1110....换算成科学记数法,小数点往前挪一位,由于只移了一位,所以指数是2,所以是1.1001 0010 0001 1111 1001 111 * 2 ^1,这样就是小数点后面23位数,前面一位数,由于前面提到所有的数都可以写成(1 + M)* 2 ^E的方式,为了省一位的空间,这里整数部分的1我们可以不计,只选尾数部分(这就是mantissa叫做尾数的原因)
所以,符号位是0,尾数位是 1001 0010 0001 1111 1001 111,接下来差的就是指数位,这里的指数位很明显是1,因为我们刚刚只往前移了一位,所以值应该就是 1,再加上127的偏移量,得到的是1 + 127 = 1000 0000 = 128
到这里就完成了,也就是说,我们自己手动换算的表示结果为:
0 1000 0000 1001 0010 0001 1111 1001 111
^ ^ ^
符号位 指数位128 尾数位
我们可以在计算机里验证一下:0100 0000 0100 1001 0000 1111 1100 1111 转换成16进制是 0xcf 0f 49 40 ,然后我们创建一个包含四个字节的byte数组,然后把里面的数字拷进一个float变量里,代码如下所示:
int main()
{
float f;
// 由于堆栈的原因,这里要倒着写
unsigned char b[4] = {
0xcf, 0x0f, 0x49, 0x40 };
memcpy(&f, &b, sizeof(f));
cout << f <<endl;
cin.get();
}
就可以看到正确的结果啦!
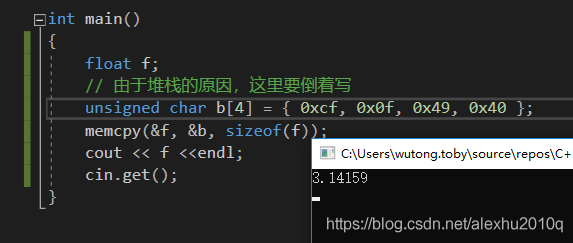
十进制数转换到浮点数
步骤如下:
- 先把数转换成二进制,根据正负得到符号位s
- 然后把小数点移到正确的位置,如果往左移了n位,则指数e为n+127,右移n为,则指数e为-n + 127
- 然后把尾数部分存到用23个bit位表示的M上
把s e 和m三个值组合起来,就是最后的浮点数了
浮点数的精度问题
32位float,即单精度浮点数的有效位数是7位到8位之间,含七个数字的数都能精确被float类型表示,但由于它是科学计数法的方式,所以当数额很大或很小的时候,会产生严重的误差。
最后关于这个E还有一点要提,这个E有两个特殊的值,处理的时候是与正常结果不一样的,就是当E= 0000 0000 或 E = 1111 1111时,根据国际标准IEEE 754规定:
当E= 0000 0000 时
指数位为0了,如下图所示,意味着这里的指数达到了最小,
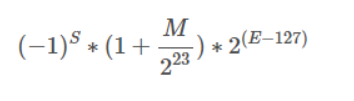
此时规定,这里的1不加了,此时的E -127不等于-127,而是等于-126,E全为0。这时,浮点数的指数E等于1-127(或者1-1023),有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
当E= 1111 1111 时
E全为1。这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示这个数不是一个数(NaN)。
最难以理解的地方:E= 0000 0000 和E = 11111111
我始终理解不了,为什么有这么古怪的规定,后来慢慢明白了,有了这些规定,尽管int类型里我们无法表示无穷大和无穷小,但是通过浮点数,我们可以处理各种各样的数据类型,都不会报错
比如在C#代码中,下述操作不会报错:
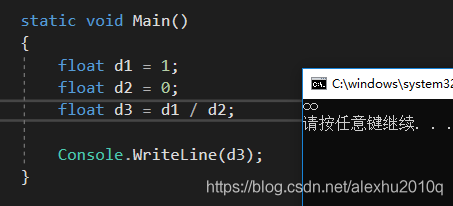
C++也是同样没问题:
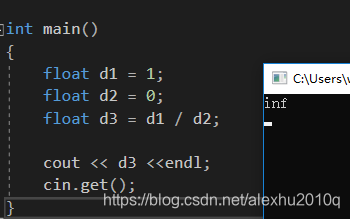
如果改变d1为0,则得到的结果是无效的,float对于这种数字,一样能处理:
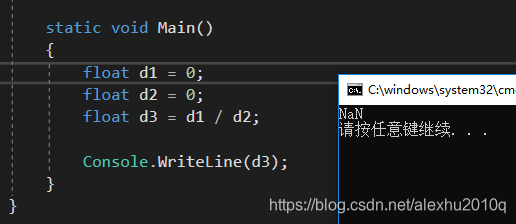
所以说,这么设计浮点数,让浮点数能够广泛应用到所有的数字中,这样设计浮点数,容错率很高
定点数
前面提到了32位浮点数,只能表示七到八位有效数字,这个数值对于稍微大一点的数字误差就很大了,而且随着浮点数的不断累加,最后的误差可能会非常大
而且各个软硬件平台没有严格遵循IEEE754的标准,所以浮点数的运算难以在不同平台上完全同步
为了解决浮点数的不确定问题,这里介绍了定点数
定点数的定点就体现在一个32位bit数的小数点的位置上,对于浮点数,其小数点可以在任何一位上
对于浮点数,如下所示
// 不考虑符号位
1 . 0000 0000 0000 0000 0000 000
^ ^ ^
第一位默认是1 一开始的小数点默认在这里 后面的23位
然后额外的八位用来表示指数位,也就是说,由指数E的数值,可以让小数点向右移动128位,或者向左移动127位
而对于定点数,这个小数点就是固定的,如下图所示:
// 不考虑符号位
// 定点数在32位平台下用第一位表示符号位,接着的21位表示整数部分,最后的10位表示小数部分
000 0000 0000 0000 0000 00 . 00 0000 0000
^ ^ ^
前面是整数位,一共21位 小数点固定在这里 后面是小数位,一共10位
可以看到,定点数相当于把原本表示整数的int,拿出了10位用来表示小数,所以定点数表示的范围会比int类型小很多,其范围在-2097152.0~2097151.990234375之间