决策树入门、sklearn实现、原理解读和算法分析

决策树入门

总算来到心心念念的决策树了。工作中一直在用xgb模型，今天开始，终于可以尝试去理解其背后的算法原理了。不过xgb较为复杂，还是先从最基础的模型入门吧：决策树。

决策树是怎么解决机器学习的问题呢？其本质是通过多层if/else去把训练集做拆分，最终得到预测结果。

举个例子说一下。我们要区分以下4种动物：熊、鹰、企鹅和海豚。此时，我们可以先做第一层if拆分: 动物是否有羽毛？有羽毛的可能是鹰或企鹅，没有羽毛的则是熊或海豚。针对有羽毛的情况，我们再做一层if判断: 动物会不会飞？会飞的是鹰，不会飞的是企鹅；针对没有羽毛的情况，我们新的if逻辑是：有没有鳍？有鳍的是海豚，没有鳍的是熊。以下为if/else操作的图示。

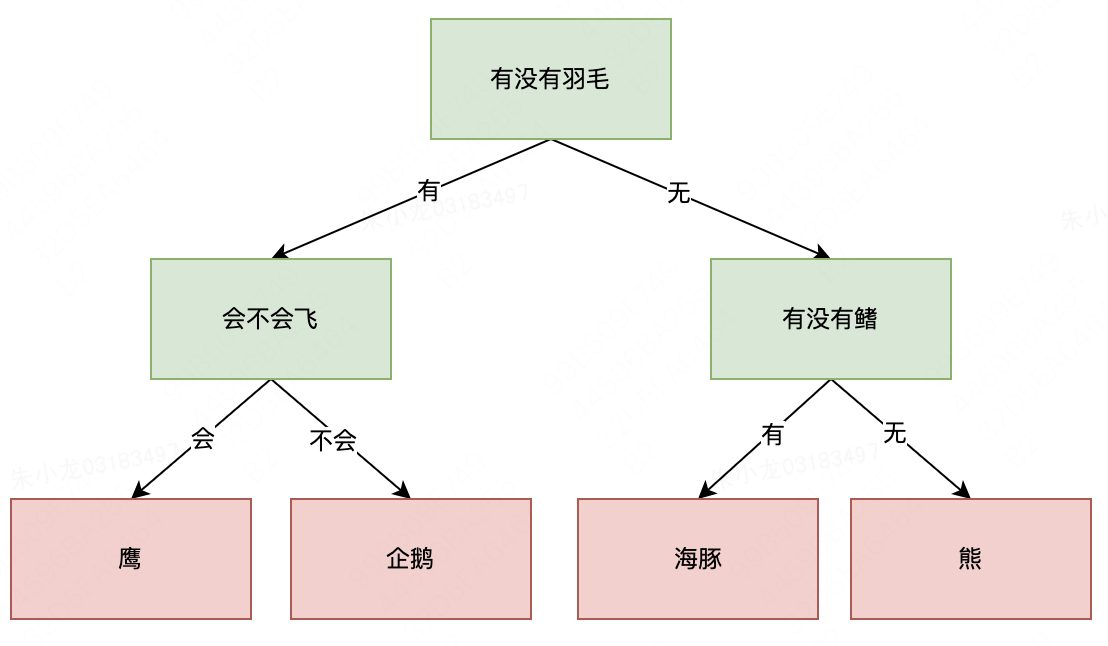
如果用机器学习的语言来描述，就是为了区分鹰、企鹅、海豚和熊这四种动物，我们使用三个特征：“有没有羽毛”、“会不会飞”和“有没有鳍”，来构建一个分类模型。

嗯，看起来还挺简单的。

决策树sklean实现

上述区分动物的实例，虽然有助于我们入门决策树，但本质是个多分类问题，和我们平时研究的二分类问题还是有些不太一样的。为了便于理解决策树的具体原理，我们最好还是找个二分类的实例。本文所使用的二分类实例的代码如下所示。

from sklearn.datasets import make_moons


def two_moons():
    # make_blobs: sklearn内置单标签类数据集
    features, labels = make_moons(n_samples=100,  noise=0.25, random_state=3)

    # discrete_scatter：数据集可视化
    plt.scatter(features[labels == 0][:, 0], features[labels == 0][:, 1])
    plt.scatter(features[labels == 1][:, 0], features[labels == 1][:, 1])
    plt.legend(['Class0', 'Class1'], loc=4)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()

    return features, labels


if __name__ == '__main__':
    X, y = two_moons()

运行代码后，可以得到下图。该问题中，有两个特征：$x$和$y$；分类结果有两个：class0和class1，分别对应蓝色和黄色圆点，样本数量均为50个。

如果要使用sklearn决策树算法对该问题进行分类，可以使用以下的代码实现：

from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt


if __name__ == '__main__':

    X, y = two_moons()
    # 3层决策树
    dtc = DecisionTreeClassifier(max_depth=3)
    dtc_tree = dtc.fit(X, y)

    # 文本形式显示决策树规则
    text_representation = tree.export_text(dtc_tree)
    print(text_representation)

    # 决策树可视化
    fig = plt.figure(figsize=(25, 20))
    _ = tree.plot_tree(
        dtc,
        filled=True
    )
    fig.savefig("decision_tree.png")

代码中，包含三段内容：(1)构造深度为3的决策树；（2）打印决策树规则；（2）决策树可视化。

运行代码后，得到决策树规则如下：

|--- feature_1 <= 0.06
|   |--- feature_0 <= -0.42
|   |   |--- class: 0
|   |--- feature_0 >  -0.42
|   |   |--- class: 1
|--- feature_1 >  0.06
|   |--- feature_0 <= 1.20
|   |   |--- feature_1 <= 0.50
|   |   |   |--- class: 0
|   |   |--- feature_1 >  0.50
|   |   |   |--- class: 0
|   |--- feature_0 >  1.20
|   |   |--- feature_0 <= 1.67
|   |   |   |--- class: 1
|   |   |--- feature_0 >  1.67
|   |   |   |--- class: 1

可视化效果如下：

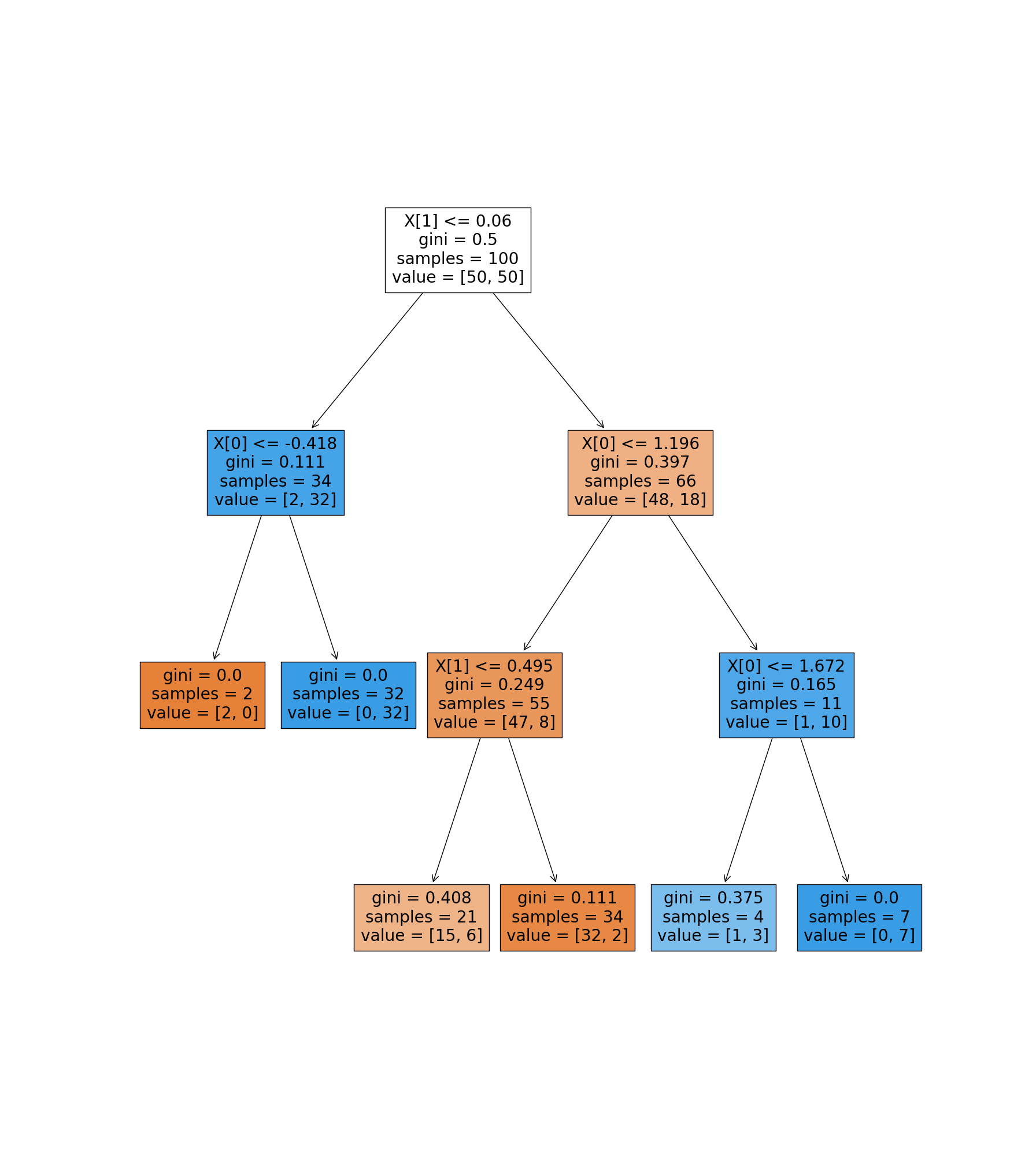
上面的结果暂时不多做解释，主要是先对分类结果有个印象。为了更容易理解分类过程，这里依次描述和绘制第1、2和3层的分类结果：

当深度只有1的时候，模型沿着$y=0.06$水平方向，将区域分为两块，上半部分为class0，下半部分为class1。

当深度为2时，模型在已有结果的基础上继续细化：上半部分沿着$x=1.20$垂直方向拆分，左边仍为class0，但是右边变为class1；下半部分沿着$x=-0.42$垂直方向拆分，左边变为class0。

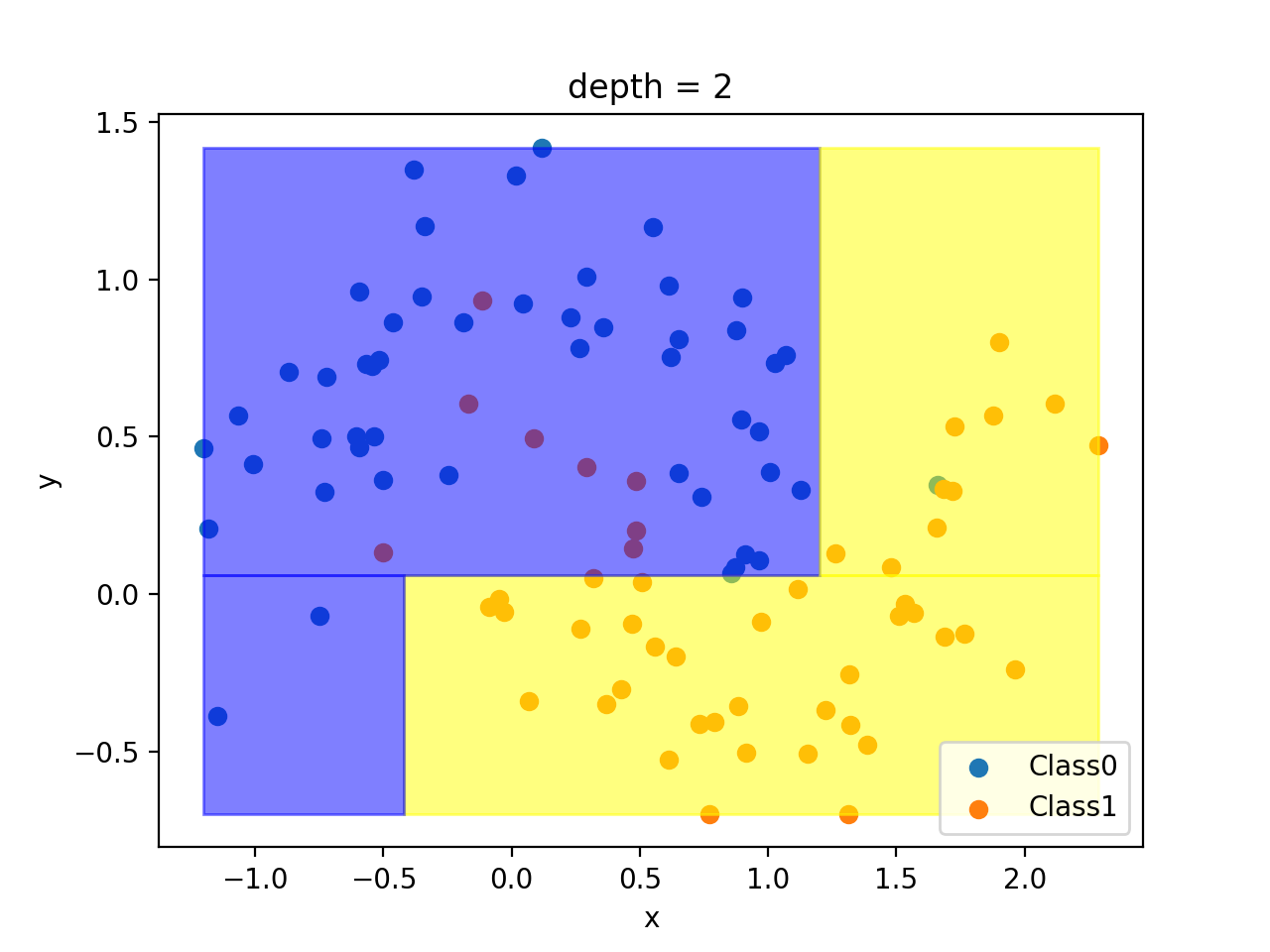
当深度变为3后，上半部分的2块区域还可以继续分割，具体方式直接看图，此处不再赘述。

决策树算法

通过第2节的描述，我们可以发现，构造决策树的核心内容至少包含两个方面：（1）每一次的区域切割方向；（2）最佳切割点。这其实是和优化思路非常类似——分别对应迭代方向和迭代步长。

单/多变量决策树

先分析清楚切割方向。从sklearn的分类流程不难看出，切割方向只会沿着x轴或者y轴，所以是“轴平行”的，专业名词为：单变量决策树。这种方式下，决策树每次只会沿着某一个特征进行拆分，而其他特征则保持不变。这就导致在遇到边界比较复杂的分类问题时，需要多次划分才可能得到比较好的近似。针对下图的实例，需要4次划分才能完全分开。

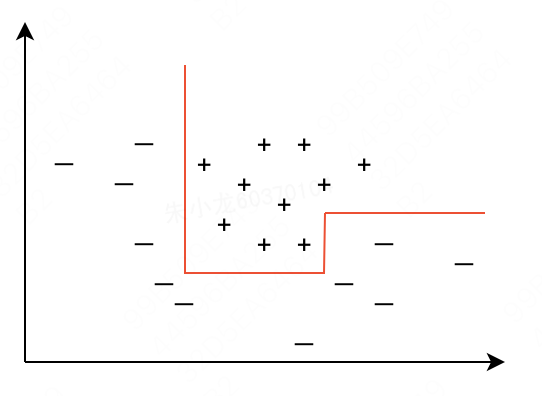
如果可以不限定沿着某个坐标轴，而是允许沿着任意方向进行切割，则可能更快完成完美的分类。如下图所示，2次便可以完成全部划分。该方式学名为多变量决策树，或斜决策树。相比单变量决策树，多变量决策树的可选切割范围有了巨大的拓展，但是最佳切割方向的寻找，也会变得更加困难。

CART分类树算法

然后再看一下最佳切割点的选取，这里需要用到一个算法：CART分类树算法。

在CART分类树算法中，使用gini（基尼系数）来衡量某一结点的纯度。结点中的样本越多属于同类，那么这个结点越“纯”，gini指标就会越小，所以gini指标也称为gini不纯度。

假设$Aj(j=1,2)$为将样本分类后的两个部分，$w_j$为这两部分的各自占比，$p_i$为样本属于第$i$类的概率，$n$为分类的总个数，那么结点$A_j$的gini不纯度可以表示为：
$$\text{gini}(A_j)=1-\sum _{i=1}^n{p}_i^2$$
整体的gini值为
$$\text{gini}(A)=\sum _{j=1}^2{w}_j\ast \text{gini}(A_j)$$
在sklearn中，实际使用是如下的一种优化版本：
$$\text{gini}=\sum _{i=1}^2{w}_i\ast (1-w_i)$$
回顾第2节的可视化效果图，我们计算一下第1和2层中的每个结点的gini值：
$${\text{gini}}_1=50/100\ast (1-50/100)\ast 2=0.5$$
$${\text{gini}}_{2左}=2/34\ast (1-2/34)+32/34\ast (1-32/34)=0.1107$$
$${\text{gini}}_{2右}=48/66\ast (1-48/66)+18/66\ast (1-18/66)=0.3967$$
可以发现，该结果和sklearn可视化图中的gini结果，完全一致。

至此，我们可以将sklearn决策树求解分类问题的算法过程理解为：首先使用单变量决策树逻辑，对所有特征逐一尝试分割；然后使用CART分类树算法确定最佳分割点，得到最小gini值，完成一次分割。此后再逐渐增加树的深度，不断细化分割，直至gini=0。

决策树分析

复杂度控制

理论上来说，决策树可以一直分割到所有叶结点都是纯的叶结点。但这很容易导致模型变得非常复杂，并且对训练数据高度过拟合。还是以文章中的实例为例：depth=3时，右上角区域被分割为了两个区域；但从我们朴素的认知来看，该区域内的class0更像是一个异常值，完全可以不再分割。

防止过拟合有两种常见的策略：一种是及早停止树的生长，也叫预剪枝，具体策略包括：限制树的最大深度、叶结点的最大数目、规定结点中数据点的最小数据等；另一种是先构造树，但随后删除或折叠信息量很少的结点，也叫后剪枝或剪枝。

需要注意的是，在sklearn中，只有预剪枝，没有后剪枝。

特征重要性

如果决策树比较深，那么查看整个树可能会比较费劲。此时，我们可以通过特征重要性来判断每个特征对树的决策的重要性。对于任意一个特征来说，它都是一个介于0和1之间的数字，其中0表示“根本没用到”，1表示“完美预测目标值”。

sklearn计算特征重要性的方式，比较简单，只需要一行代码：

# 特征重要性
feat_importance = dtc_tree.tree_.compute_feature_importances(normalize=False)

运行后，可以得到特征$x$和$y$的重要性值分别为0.1477和0.2139。

接下来，我们主要看一看特征重要性的计算原理：
$$N_t/N\times (\text{gini}-N_{tL}/N_t{\text{gini}}_L-N_{tR}/N_t{\text{gini}}_R)$$
其中，N_t是当前结点的样本数目，N是样本的总数，$\text{gini}$是当前结点的基尼系数，${\text{gini}}_L$和${\text{gini}}_R$分别是结点左和右孩子的基尼系数，$N_{tL}$和$N_{tR}$是对应的样本数目。

在本文的分类实例中，3次用到$x$，2次用到$y$。首先计算特征$x$的重要性
$$F{i}_{x1}=34/100\ast (0.111-0-0)$$
$$F{i}_{x2}=66/100\ast (0.397-0.249\ast 55/66-0.165\ast 11/66)$$
$$F{i}_{x3}=11/100\ast (0.165-0.375\ast 4/11)$$
因此特征$x$的重要性为
$$F{i}_x=F{i}_{x1}+F{i}_{x2}+F{i}_{x3}=0.1478$$
照葫芦画瓢，可以得到特征$y$的重要性为
$$F{i}_{y1}=100/100\ast (0.5-0.111\ast 34/100-0.397\ast 66/100)$$
$$F{i}_{y2}=55/100\ast (0.249-0.408\ast 21/55-0.111\ast 34/55)$$
$$F{i}_y=F{i}_{y1}+F{i}_{y2}=0.2138$$
显然，和sklearn的重要性值结果是相同的。

决策树特点

相比其他机器学习算法，决策树的优点有两个：（1）模型很容易可视化，可以输出特征重要性值，非专家也很容易理解；（2）算法不受数据缩放的影响，因此无需对数据进行归一化等预处理操作。

决策树的一个重要特质是不能外推，即无法在训练数据之外生成”新的”数据。以下图为例，横轴是年份，纵轴是当年1兆字节(MB)RAM的价格。训练集中包含了2000年前的历史数据，目前要预测2000年后的价格。如果使用线性模型，会得到价格持续降低的结果；而如果使用决策树模型，此后价格会维持2000年的价格不变。显然，从合理性的角度来看，线性模型比决策树模型更适合求解该问题。