一、粒子群算法理论
粒子群算法来源于鸟类集体活动的规律性,进而利用群体智能建立简化模型。它模拟的是鸟类的觅食行为,将求解问题的空间比作鸟类飞行的时间,每只鸟抽象成没有体积和质量的粒子,来表征一个问题的可行解。
1.1 粒子群算法建模
粒子群算法首先在给定的解空间中随机初始化粒子群,待优化问题的变量数决定了解空间的维数。每个粒子有了初始位置与初始速度,然后迭代寻优。每一次迭代中,每个粒子通过跟踪两个极值来更新自己的解空间中的位置和速度,一个是单个粒子本身在迭代中找到的最优粒子(个体极值),一个是所有粒子在迭代过程中的最优解粒子(全局极值)。
1.2 粒子群算法特点
(1)基于群体智能理论的优化算法,高效的并行算法。
(2)粒子群算法随机初始化种群,使用适应值来评价个体的优劣程度,进行一系列的随机搜索。但粒子群算法根自己的速度来决定搜索,不需要进行交叉变异等操作,避免了复杂的操作。
(3)每个粒子在算法结束时仍保持个体极值,所以除了得到问题的最优解以外,还能得到若干次优解,给出更多方案。
(4)粒子群算法特有的记忆使其可以动态的跟踪当前搜索情况并调整搜索方向。
二、粒子群算法种类
2.1 基本粒子群算法
假设在一个D维的目标搜索空间中,有N个粒子组成群落,其中第i个粒子表示为一个D维向量:
第i个粒子飞行速度也是一个D维向量:
第i个粒子迄今为止搜索到最优位置称为个体极值:
整个粒子群迄今为止搜索到的最优位置为全局极值:
在找到这两个最优值后,粒子群更新自己的速度和位置:
其中,c1,c2 是学习因子(加速常数);r1,r2 为[0,1]范围内的均匀随机数;vij⊆[−vmax,vmax] 是粒子速度; r1,r2 增加了粒子飞行的随机性。更新速度的式子由三部分组成,第一部分为‘惯性’,反应了粒子群运动的‘习惯’;第二部分是‘认知’,反映了对自身历史经验的记忆;第三部分是‘社会’,反映了粒子间协同合作知识共享的群体历史经验。
2.2 标准粒子算法
引入了两个新的概念:
探索:指粒子在一定程度上离开原先的轨迹,向新的方向搜索,体现了开拓未知区域的能力,探索能力是全局搜索能力。
开发:指粒子在一定程度上继续在原先的轨迹上进行进一步搜索,是局部搜索能力。
1998年,Shi Yuhui等人提出了带有惯性权重的改进粒子群算法:
第一个式子有三个部分,第一部分保证算法的全局收敛性,第二、三部分保证局部收敛能力。w较大,全局收敛能力强局部收敛能力减弱;w较小,全局收敛能力减弱,局部收敛能力较强。当w=1时,与基本粒子算法相同,实验结果表明:w在0.8~1.2之间有更快的收敛速度,w>1.2时,容易陷入局部极值。
在搜索时还可以对w进行动态调整,采用较多的是Shi提出的线性递减权值策略:
Tmax 表示最大进化代数;wmax 表示惯性最大权重;wmin 表示惯性最小权重。
2.3 压缩粒子群算法
Clerc等人利用约束因子来控制最终的收敛,可以有效搜索不同区域:
λ 为压缩因子:
实验结果表明:与使用惯性权重的粒子群算法比较,使用具有压缩因子的粒子群算法有更快的收敛速度。
2.4 离散粒子群算法
Kennefy和Eberhart提出了离散二进制版的粒子群算法。将离散的问题映射到了连续的粒子运动空间,计算上扔保留速度-位置更新的运算规则。粒子在空间状态的取值只限于0,1两个值,而速度的每一维 vij 代表每一位 xij 取值为1的可能性,因此 vij 的公式保持不变,但是 pbest 和 gbest 只能在[0,1]之间取值:

r是从 U(0,1) 分布产生的随机数。
三、粒子群算法流程

四、MATLAB实例及仿真
参数说明:
粒子种群规模N:一般为100~200。
惯性权重w:控制算法的开发和探索能力,一般取值为[0.8,1.2]。
加速常数 c1,c2 :调节向 pbest和pbest 方向飞行的最大步长,分别决定了粒子个体经验和群体经验对粒子运动轨迹的影响。 c1=0 粒子缺乏认知能力, c2=0 个体之间没有信息交互,所以一般设置 c1=c2 ,通常取 c1=c2=1.5 。这样个体经验和群体经验有了同样的影响力。
粒子最大速度 vmax :粒子速度在每一维都有一个最大速度限制值,用来对粒子速度进行钳制,该值太大,粒子也许会飞过优秀区域,太小粒子们可能会陷入局部最优,无法移动足够远跳出局部最优。研究发现 设定vmax 和调整惯性权重的作用是等效的,所以 vmax 一般用于初始化进行设定,二不再对最大速度进行细致的选择和调节。
邻域结构设定:全局版的粒子群算法将整个群体作为粒子的邻域,具有搜索快的优点但是容易陷入局部最优。局部版本粒子群算法将位置相近的个体作为粒子的邻域,收敛速度慢,不易陷入局部最优。实际中可先采用全局粒子群算法寻找最优解方向,再采用局部粒子群算法细致搜索。
边界条件处理:边界吸收的方法。
例1
计算函数的最小值,其中个体x的维数n=10,这是一个简单的平方和函数,只有一个极小点x=(0,0,...,0),理论上最小值分f(0,0,...,0)=0。
解:
clear all;
close all;
clc;
N=100; %群体粒子个数
D=10; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
w=0.8; %惯性权重
Xmax=20; %位置最大值
Xmin=-20; %位置最小值
Vmax=10; %速度最大值
Vmin=-10; %速度最小值
%初始化个体
x=rand(N,D)*(Xmax-Xmin)+Xmin;
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%初始化个体最优位置和最优值
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)=func1(x(i,:));
end
%初始化全局最优位置和最优值
g=ones(1,D);
gbest=inf;
for i=1:N
if (pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%按照公式依次迭代直到满足精度或者迭代次数
for i=1:T
for j=1:N
if (func1(x(j,:))<pbest(j))
p(j,:)=x(j,:);
pbest(j)=func1(x(j,:));
end
if (pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:)=x(j,:)+v(j,:);
%边界条件处理
for ii=1:D
if (v(j,ii)<Vmin)||(v(j,ii)>Vmax)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
if (x(j,ii)<Xmin)|(x(j,ii)>Xmax)
x(j,ii)=rand*(Xmax-Xmin)+Xmin;
end
end
end
%记录全局最优值
gb(i)=gbest;
end
g; %最优个体
gb(end); %最优值
figure
plot(gb)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度进化曲线')
%适应度函数
function result=func1(x)
summ=sum(x.^2);
result=summ;
end
例2
求函数 的最小值,其中x的取值范围是[-4,4],y的取值范围是[-4,4]。这是一个有多个局部极值的函数。函数图形如图:
clear all;
close all;
clc;
x=-4:0.02:4;
y=-4:0.02:4;
N=size(x,2);
for i=1:N
for j=1:N
z(i,j)=3*cos(x(i)*y(j))+x(i)+y(j)*y(j);
end
end
mesh(x,y,z)
xlabel('x')
ylabel('y')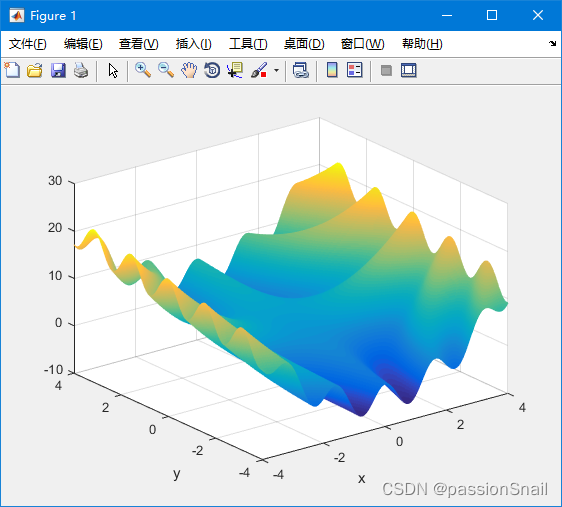
解:
clear all;
close all;
clc;
N=100; %群体粒子个数
D=2; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
Wmax=0.8; %惯性权重最大值
Wmin=0.4; %惯性权重最小值
Xmax=4; %位置最大值
Xmin=-4; %位置最小值
Vmax=1; %速度最大值
Vmin=-1; %速度最小值
%初始化个体
x=rand(N,D)*(Xmax-Xmin)+Xmin;
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%初始化个体最优位置和最优值
p=x;
pbest=ones(1,D);
for i=1:N
pbest(i)=func2(x(i,:));
end
%初始化全局最优位置和最优值
g=ones(1,D);
gbest=inf;
for i=1:N
if (pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%按照公式依次迭代直到满足精度或者迭代次数
for i=1:T
for j=1:N
%更新个体最优位置和最优值
if (func2(x(j,:))<pbest(j))
p(j,:)=x(j,:);
pbest(j)=func2(x(j,:));
end
%更新全局最优位置和最优值
if (pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
%计算动态惯性权重值
w=Wmax-(Wmax-Wmin)*i/T;
%更新位置和速度
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:)=x(j,:)+v(j,:);
%边界条件处理
for ii=1:D
if (v(j,ii)<Vmin)||(v(j,ii)>Vmax)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
if (x(j,ii)<Xmin)||(x(j,ii)>Xmax)
x(j,ii)=rand*(Xmax-Xmin)+Xmin;
end
end
end
gb(i)=gbest;
end
g;%最优个体
gb(end);%最优值
figure
plot(gb)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度进化曲线')
%适应度函数
function value=func2(x)
value=3*cos(x(1)*x(2))+x(1)+x(2)^2;
end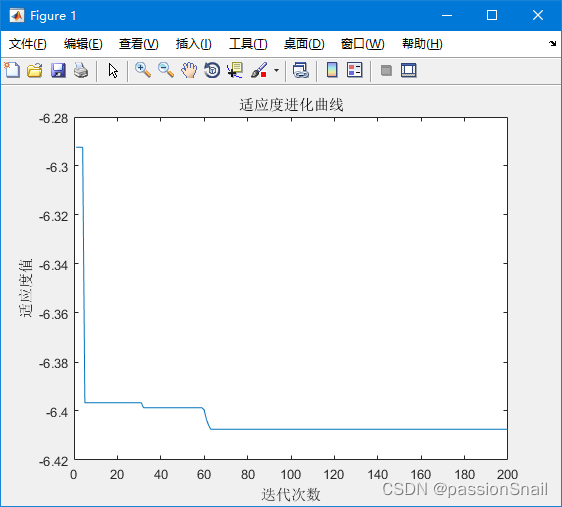
例3
用离散粒子群算法求函数的最小值,其中x的取值范围是[0,9],这是一个有局部多个极值的函数,图形如图所示:
clear all;
close all;
clc;
x=0:0.01:9;
y=x+6*sin(4*x)+9*cos(5*x);
plot(x,y)
xlabel('x')
ylabel('f(x)')
解:
clear all;
close all;
clc;
N=100; %群体粒子个数
D=20; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
Wmax=0.8; %惯性权重最大值
Wmin=0.4; %惯性权重最小值
Xs=9; %位置最大值
Xx=0; %位置最小值
Vmax=10; %速度最大值
Vmin=-10; %速度最小值
%初始化个体
x=randi([0,1],N,D);
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%初始化个体最优位置和最优值
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)=func3(x(i,:),Xs,Xx);
end
%初始化全局最优位置和最优值
g=ones(1,D);
gbest=inf;
for i=1:N
if (pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%按照公式依次迭代直到满足精度或者迭代次数
for i=1:T
for j=1:N
%更新个体最优位置和最优值
if (func3(x(j,:),Xs,Xx)<pbest(j))
p(j,:)=x(j,:);
pbest(j)=func3(x(j,:),Xs,Xx);
end
%更新全局最优位置和最优值
if (pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
%计算动态惯性权重值
w=Wmax-(Wmax-Wmin)*i/T;
%更新位置和速度
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
%边界条件处理
for ii=1:D
if (v(j,ii)<Vmin)||(v(j,ii)>Vmax)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
end
vx(j,:)=1./(1+exp(-v(j,:)));
for jj=1:D
if vx(j,jj)>rand
x(j,jj)=1;
else
x(j,jj)=0;
end
end
end
gb(i)=gbest;
end
g;%最优个体
m=0;
for j=1:D
m=g(j)*2^(j-1)+m;
end
f1=Xx+m*(Xs-Xx)/(2^D-1);%最优值
figure
plot(gb)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度进化曲线')
%适应度函数
function result=func3(x,Xs,Xx)
m=0;
D=length(x);
for j=1:D
m=x(j)*2^(j-1)+m;
end
f=Xx+m*(Xs-Xx)/(2^D-1);%译码成十进制数
fit=f+6*sin(4*f)+9*cos(5*f);
result=fit;
end
例4
0-1背包问题,有N件物品和容积为V的包,第i件物品的容积是c(i),价值是w(i),求将这些物品放入包中,使物体的总容积不超过背包容积,且总价值和最大。假设物品数量为10,背包容量为300.每件物品的体积为[95,75,23,73,50,22,6,57,89,98];价值为[89,59,19,43,100,72,44,16,7,64];
解:
clear all;
close all;
clc;
N=100; %群体粒子个数
D=10; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
Wmax=0.8; %惯性权重最大值
Wmin=0.4; %惯性权重最小值
Vmax=10; %速度最大值
Vmin=-10; %速度最小值
V=300; %背包容量
C=[95,75,23,73,50,22,6,57,89,98]; %物品体积
W=[89,59,19,43,100,72,44,16,7,64]; %物品价值
afa=2; %惩罚函数系数
%初始化个体
x=randi([0,1],N,D);
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%初始化个体最优位置和最优值
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)=func4(x(i,:),C,W,V,afa);
end
%初始化全局最优位置和最优值
g=ones(1,D);
gbest=eps;
for i=1:N
if (pbest(i)>gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%按照公式依次迭代直到满足精度或者迭代次数
for i=1:T
for j=1:N
%更新个体最优位置和最优值
if (func4(x(j,:),C,W,V,afa)>pbest(j))
p(j,:)=x(j,:);
pbest(j)=func4(x(j,:),C,W,V,afa);
end
%更新全局最优位置和最优值
if (pbest(j)>gbest)
g=p(j,:);
gbest=pbest(j);
end
%计算动态惯性权重值
w=Wmax-(Wmax-Wmin)*i/T;
%更新位置和速度
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
%边界条件处理
for ii=1:D
if (v(j,ii)<Vmin)||(v(j,ii)>Vmax)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
end
vx(j,:)=1./(1+exp(-v(j,:)));
for jj=1:D
if vx(j,jj)>rand
x(j,jj)=1;
else
x(j,jj)=0;
end
end
end
gb(i)=gbest;
end
g;%最优个体
figure
plot(gb)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度变化曲线')
%适应度函数
function result=func4(f,C,W,V,afa)
fit=sum(f.*W);
TotalSize=sum(f.*C);
if TotalSize<=V
fit=fit;
else
fit=fit-afa*(TotalSize-V);
end
result=fit;
end
参考资料《智能优化算法及Matlab实例》