第一章、AI人工智能入门之梯度下降及一元线性回归(2)
目录
一、线性回归是什么?
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归(一元回归),大于一个自变量情况的叫做多元回归。
线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。这是因为线性依赖于其未知参数的模型比非线性依赖于其未知参数的模型更容易拟合,而且产生的估计的统计特性也更容易确定。
线性回归模型经常用最小二乘逼近来拟合,但他们也可能用别的方法来拟合,比如用最小化“拟合缺陷”在一些其他规范里(比如最小绝对误差回归),或者在桥回归中最小化最小二乘损失函数的惩罚.相反,最小二乘逼近可以用来拟合那些非线性的模型.因此,尽管“最小二乘法”和“线性模型”是紧密相连的,但他们是不能划等号的。
二、线性回归的应用
数学
线性回归有很多实际用途。分为以下两大类:
-
如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
-
给定一个变量y和一些变量X1,...,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与Xj之间相关性的强度,评估出与y不相关的Xj,并识别出哪些Xj的子集包含了关于y的冗余信息。
趋势线
一条趋势线代表着时间序列数据的长期走势。它告诉我们一组特定数据(如GDP、石油价格和股票价格)是否在一段时期内增长或下降。虽然我们可以用肉眼观察数据点在坐标系的位置大体画出趋势线,更恰当的方法是利用线性回归计算出趋势线的位置和斜率。
流行病学
有关吸烟对死亡率和发病率影响的早期证据来自采用了回归分析的观察性研究。为了在分析观测数据时减少伪相关,除最感兴趣的变量之外,通常研究人员还会在他们的回归模型里包括一些额外变量。例如,假设我们有一个回归模型,在这个回归模型中吸烟行为是我们最感兴趣的独立变量,其相关变量是经数年观察得到的吸烟者寿命。研究人员可能将社会经济地位当成一个额外的独立变量,已确保任何经观察所得的吸烟对寿命的影响不是由于教育或收入差异引起的。然而,我们不可能把所有可能混淆结果的变量都加入到实证分析中。例如,某种不存在的基因可能会增加人死亡的几率,还会让人的吸烟量增加。因此,比起采用观察数据的回归分析得出的结论,随机对照试验常能产生更令人信服的因果关系证据。当可控实验不可行时,回归分析的衍生,如工具变量回归,可尝试用来估计观测数据的因果关系。
金融
资本资产定价模型利用线性回归以及Beta系数的概念分析和计算投资的系统风险。这是从联系投资回报和所有风险性资产回报的模型Beta系数直接得出的。
经济学
线性回归是经济学的主要实证工具。例如,它是用来预测消费支出,固定投资支出,存货投资,一国出口产品的购买,进口支出,要求持有流动性资产,劳动力需求、劳动力供给。
三、线性回归的一般形式
一元线性回归分析:Y=a+bx
多元线性回归分析:Y=a+b1X1+
6X2+..·+bkXk
渐进回归模型:Y=a+be-ry
二次曲线回归模型:Y=a+bX +bX2双曲线模型:Y=a+fracb]
除此之外还有其他的非线性回归分析的一般形式,这里不再赘述
四、一元线性回归函数的推导过程

最小二乘法手工推导:

构造损失函数及推导(梯度下降法):

梯度下降法和最小二乘法
相同点:
本质和目标相同:两种方法都是经典的学习算法,在戈丁已知数据的前提下利用求导算出一个模型(函数),使得损失函数最小,然后对给定的新数据进行估算预测
不同点:
损失函数:梯度下降可以选取其他损失函数,而最小二乘一定是平方损失函数
实现方法:最小二乘法是直接求导找出全局最小;而梯度下降是一种迭代法
效果:最小二乘法找到的一定是全局最小,但计算繁琐,且复杂情况下未必有解;梯度下降迭代计算简单,但找到的一般是局部最小,只有在目标函数是凸函数时才是全局最小;到最小点附近时收敛速度会变慢,且对初始点的选择极为敏感
五、相关代码(python)
梯度下降:
y=(x-2.5)^2-1
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-1,6,141)
y=(x-2.5)**2-1
#每点梯度 求导
def dj(theta) :
return 2*(theta-2.5)
#每点的Y值
def J(theta):
try:
return (theta-2.5)**2-1
#防止了越来越大
except:
return float('inf')
#梯度下降,将theta的值记录下来,定义展大送代次数和允许的最小误差
def gradient_descent(initial_theta,eta,n_iters=1e4,error=1e-8):
theta=initial_theta
theta_hist.append(initial_theta)
i_iter=0
while i_iter<n_iters:
gradient=dj(theta)
last_theta=theta
theta=theta-eta*gradient
theta_hist.append(theta)
if abs(J(theta)-J(last_theta))<error:
break
i_iter+=1
#绘制原始曲线和梯度下降的过程
def plot_thetahist():
plt.plot(x,J(x))
plt.plot(np.array(theta_hist),J(np.array(theta_hist)),color='r',marker='+')
plt.show()
#学习率,步长
eta=0.1
theta_hist=[]
gradient_descent(0,eta,n_iters=10)
plot_thetahist()当eta=0.1时

当eta=0.4时
当eta=1.1时
对比发现:步长越大,振荡越厉害,效果越不好
关于广告和汽车的一元线性回归:

import numpy as np
import matplotlib.pyplot as plt
# ---------------1. 准备数据----------
data = np.array([[1, 14],
[3, 24],
[2, 18],
[1, 17],
[3, 27]])
# 提取data中的两列数据,分别作为x,y
x = data[:, 0]
y = data[:, 1]
# 用plt画出散点图
# plt.scatter(x, y)
# plt.show()
# -----------2. 定义损失函数 均方误差 ------------------
# 损失函数是系数的函数,另外还要传入数据的x,y
def compute_cost(w, b, points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = points[i, 0]
y = points[i, 1]
total_cost += (y - w * x - b) ** 2
return total_cost / M
# ------------3.定义算法拟合函数-----------------
# 先定义一个求均值的函数
def average(data):
sum = 0
num = len(data) #返回对象的长度
for i in range(num):
sum += data[i]
return sum / num
# 定义核心拟合函数
def fit(points):
M = len(points)
x_bar = average(points[:, 0])
sum_yx = 0
sum_x2 = 0
sum_delta = 0
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_yx += y * (x - x_bar)
sum_x2 += x ** 2
# 根据公式计算w
w = sum_yx / (sum_x2 - M * (x_bar ** 2))
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_delta += (y - w * x)
b = sum_delta / M
return w, b
# ------------4. 测试------------------
w, b = fit(data)
print("w is: ", w)
print("b is: ", b)
cost = compute_cost(w, b, data)
print("cost is: ", cost)
# ---------5. 画出拟合曲线------------
plt.scatter(x, y)
# 针对每一个x,计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()运行结果:

同理关于身高和体重的(原理与上个相同):
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 4 17:16:29 2023
@author: Lenovo
"""
import numpy as np
import matplotlib.pyplot as plt
# ---------------1. 准备数据----------
data = np.array([[160, 58],
[165, 63],
[158, 57],
[172, 65],
[159, 62],
[176, 66],
[160, 58],
[162, 59],
[171, 62]])
# 提取data中的两列数据,分别作为x,y
x = data[:, 0]
y = data[:, 1]
# 用plt画出散点图
plt.scatter(x, y)
plt.show()
# -----------2. 定义损失函数 均方误差------------------
# 损失函数是系数的函数,另外还要传入数据的x,y
def compute_cost(w, b, points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = points[i, 0]
y = points[i, 1]
total_cost += (y - w * x - b) ** 2
return total_cost / M
# ------------3.定义算法拟合函数-----------------
# 先定义一个求均值的函数
def average(data):
sum = 0
num = len(data)
for i in range(num):
sum += data[i]
return sum / num
# 定义核心拟合函数
def fit(points):
M = len(points)
x_bar = average(points[:, 0])
sum_yx = 0
sum_x2 = 0
sum_delta = 0
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_yx += y * (x - x_bar)
sum_x2 += x ** 2
# 根据公式计算w
w = sum_yx / (sum_x2 - M * (x_bar ** 2))
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_delta += (y - w * x)
b = sum_delta / M
return w, b
# ------------4. 测试------------------
w, b = fit(data)
print("w is: ", w)
print("b is: ", b)
cost = compute_cost(w, b, data)
print("cost is: ", cost)
# ---------5. 画出拟合曲线------------
plt.scatter(x, y)
# 针对每一个x,计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()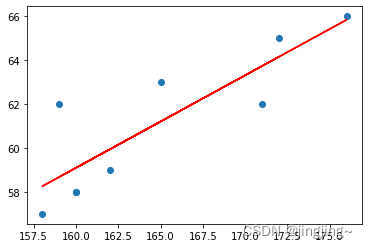
![]()
六、过拟合和欠拟合问题
欠拟合: 训练集的预测值,与训练集的真实值有不少的误差,称之为欠拟合。
过拟合: 训练集的预测值,完全贴合训练集的真实值,称之为过拟合。
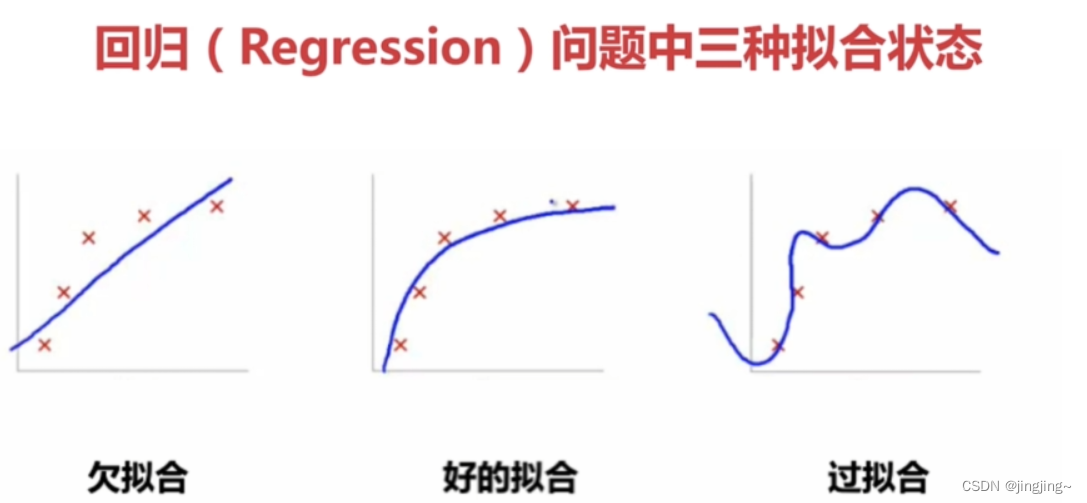


过拟合是训练集很好但到测试集不管用了
如何去避免过拟合:
加入正则项L1,L2(带平方的,将高阶系数减小)。

正则项L2推导:



参考文献
[EB/OL].https://baike.baidu.com/tem/%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92/8190345
[EB/OL].https://jiang-hs.gitee.io/posts/202f1f0f/,2021-3-6
[EB/OL].https://gitee.com/liyongfei_151/ml-course-share/tree/main/SimpleLinearRegression,2022-8-7
[EB/OL].AI-4-回归-总结-20210128_190020_哔哩哔哩_bilibili,2021-1-28
[EB/OL].https://blog.csdn.net/hyunbar/article/details/106294557,2020-5-22


