这一篇博客的主要内容在于,介绍RLWE问题以及它满足的困难性。
首先,看一下分圆多项式。这个没啥好说的,我在我的往期博客里写过。

需要提一嘴的就是 Z [ ξ ] ≅ Z [ X ] / Φ m ( X ) \mathbb{Z}[\xi] \cong \mathbb{Z}[X]/\Phi_m(X) Z[ξ]≅Z[X]/Φm(X)。这个式子的意义在于用 Φ m \Phi_m Φm的根做插值可以唯一确定 Z [ X ] / Φ m ( X ) \mathbb{Z}[X]/\Phi_m(X) Z[X]/Φm(X)里的元素,或者说,这两个结构是同构的。
本来以为 Z [ ξ ] \mathbb{Z}[\xi] Z[ξ]是插值结果,再一看是个多项式线性空间,只不过最高次数被限制为n-1。
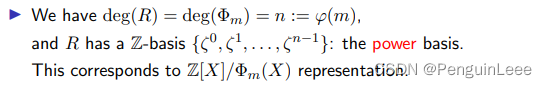
于是由于同构,我们可以规定 R R R的次数为 Φ m \Phi_m Φm的次数。
可以对线性空间 Z [ ξ ] \mathbb{Z}[\xi] Z[ξ] 指定幂基(power basis)。

在 m m m 为素数方幂的情况下,分圆多项式长得还比较标致。
对于一般的 m m m ,就不太行了。

说真的,上面这个话说得不明不白的…不妨看一下我下面的解释和例子。
我们要实现的是上面胶片里所说的线性映射:
σ : R → C n \sigma: R \rightarrow C^n σ:R→Cn
映射是线性的,意味着我们只需要确定基的映射方式,比如power basis,就知道全空间的映射方式。
举个例子,在空间 R = Z [ X ] / ( 1 + X 2 ) R=\mathbb Z[X]/(1+X^2) R=Z[X]/(1+X2)上, m = 4 m=4 m=4,power basis就是 1 和 X X X 。 Z 2 ∗ = { 0 , 1 } Z^*_2 = \{0, 1\} Z2∗={ 0,1}, ξ = i , − i \xi = i, -i ξ=i,−i。
在我看来,这两张胶片写得可以说是十分辣鸡了。这个自然嵌入映射 σ \sigma σ,本质上就是给定一个 R R R 里的多项式 p p p,你把所有的本原根 ξ \xi ξ 代进去得到 p ( ξ ) p(\xi) p(ξ)。
比如我们看下面的例一。 对多项式 1 1 1和 X X X进行自然嵌入,就是把 ξ = i , − i \xi = i, -i ξ=i,−i 代入变量 X X X,得到向量(分别是(1, 1)和(i, -i))。

再看下面的例二。当 m = 3 m=3 m=3 时, ξ = ( − 1 + 3 i ) / 2 , ( − 1 − 3 i ) / 2 \xi = (-1+\sqrt 3i)/2, (-1-\sqrt 3i)/2 ξ=(−1+3i)/2,(−1−3i)/2。分别代入1和 X X X可得。

理想格。

理想是一个环上的子集,加法封闭在理想本身中,乘法封闭在环上。
于是由于正则嵌入的引入,我们就可以把LWE困难问题放到多项式环上了。
上图说的是,我们在 R = Z [ X ] / ( 1 + X 2 ) R=\mathbb Z[X]/(1+X^2) R=Z[X]/(1+X2)上,已经把1和 X X X做了嵌入。 1 1 1和 X X X的线性组合已经在 R R R里构成了一个格,那么他们在自然嵌入后的向量空间里也构成了一个格。 1 1 1和 X X X已经是 R R R的基了,那么嵌入后的东西也是向量格的基了。
X − 2 X-2 X−2和 − 3 X + 1 -3X+1 −3X+1是格 < X − 2 , 3 X − 1 > <X-2, 3X-1> <X−2,3X−1>上的理想。所以 < X − 2 , 3 X − 1 > <X-2, 3X-1> <X−2,3X−1>也叫理想格。这个理想格是 < 1 , X > <1, X> <1,X>的子格。
于是我们可定义Ring-LWE问题。



